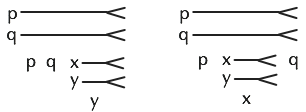Аллигаторы и их яйца
Материалы[править | править код]
Шаг 1: Распечатайте этот PDF-файл на шести или более листах цветной бумаги разных цветов.
Шаг 2: Распечатайте этот PDF-файл на нескольких листах обычной бумаги.
Шаг 3: Вырежьте из бумаги все напечатанные элементы игры!
Правила[править | править код]
Элементы игры[править | править код]
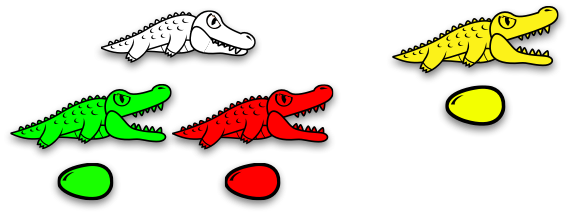
Вот голодные аллигаторы:
Голодные аллигаторы голодны. Они пожирают всё, что находится перед ними! Но они также являются весьма ответственными, поэтому они всегда охраняют свои семьи.
Это старые аллигаторы:
Старые аллигаторы не голодны. Они уже достаточно поели на своём веку. Всё, что они делают, так это охраняют свои семьи.
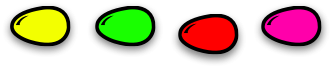
А это яйца:
Из яиц вылупляются новые семьи аллигаторов!
Семьи аллигаторов[править | править код]
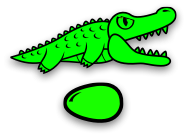
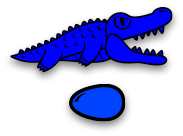
Вот маленькая семья аллигаторов:
Зелёный аллигатор охраняет зелёное яйцо.
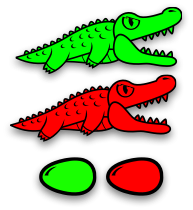
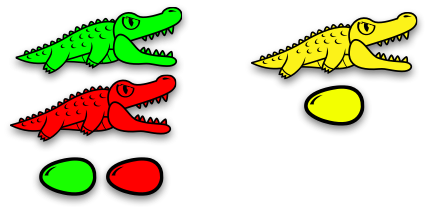
А вот семья аллигаторов чуточку побольше:
Зелёный аллигатор и красный аллигатор охраняют зелёное и красное яйцо. Или можно сказать иначе: зелёный аллигатор охраняет красного аллигатора, красный аллигатор охраняет яйца.
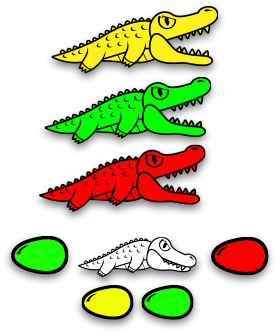
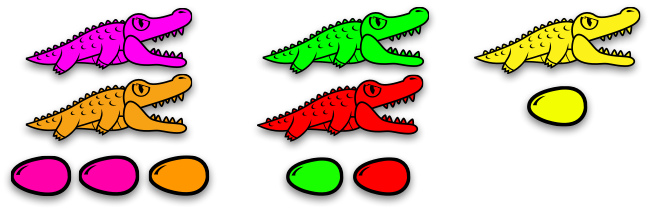
Вот огромная семья!
У нас здесь живут жёлтый, зелёный и красный аллигаторы, которые охраняют свою семью. Они охраняют три вещи: зелёное яйцо, старого аллигатора и красное яйцо. Старый аллигатор охраняет жёлтое яйцо и зелёное яйцо.
Необходимо отметить, что у яиц может быть только такой цвет, который имеется у какого-либо из аллигаторов, которые их охраняют. Невозможно иметь синее яйцо без того, чтобы синий аллигатор его охранял.
Пожирание[править | править код]
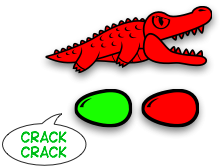
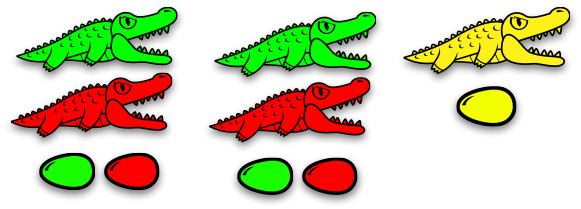
Теперь поговорим о вещах, которые не очень приятны. Вот две семьи друг около друга:
Зелёный аллигатор действительно очень голоден. А перед его ртом находится семья жёлтых аллигаторов, которая выглядит очень аппетитно!
Я думаю, что Вы предполагаете, что произойдёт далее.
К сожалению, глаза зелёного аллигатора видят больше, чем может поглотить его желудок. Он съел так много!
Итак он умер и перенёсся в рай для аллигаторов. Но история на этом не заканчивается. Из-за того, что зелёный аллигатор умер его зелёное яйцо начинает вылупляться...
Чудесным образом из него вылупилось как раз то, что зелёный аллигатор съел. Это же чудо самой жизни!
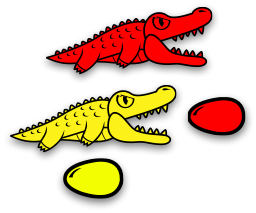
Теперь можно спуститься на одну семью вниз. У нас есть красный аллигатор, который охраняет жёлтого аллигатора и красное яйцо. Жёлтый же аллигатор охраняет своё жёлтое яйцо.
Но жёлтый же аллигатор голоден, а перед ним лежит красное яйцо. И всё начинается сначала…
Бедный аллигатор. Даже одно яйцо — это слишком много для его желудка!
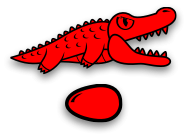
Жёлтый аллигатор умирает… Но опять, жёлтое яйцо начинает вылупляться…
И из него вылупилось как раз то, что съел жёлтый аллигатор!
Теперь нет ничего, что можно было бы скушать, а потому процесс останавливается.
Правило пожирания[править | править код]
Это был пример первого правила игры: правила пожирания.
Правило пожирания гласит, что если семьи аллигаторов находятся друг около друга…
Самый крайний левый аллигатор наверху пожирает семью, которая находится перед ним.
После этого аллигатор умирает. Но если он охранял яйца такого же цвета, как и он сам, из всех (именно так — из каждого) вылупляется то, что аллигатор съел.
Правило замены цветов[править | править код]
Продолжим рассматривать вышеприведённый пример — оранжевый аллигатор пожирает жёлтую семью, оставляя после себя:
Теперь зелёный аллигатор в верхнем левом углу хочет пожрать семью, которая находится перед ним. Но перед тем, как он сделает это, необходимо рассмотреть правило замены цветов.
Это правило гласит, что если аллигатор собирается съесть семью, в которой есть аллигаторы и яйца таких же цветов, какие есть и в его собственной семье, необходимо заменить все такие цвета в поедаемой семье на какие-нибудь другие, которых нет в исходной семье.
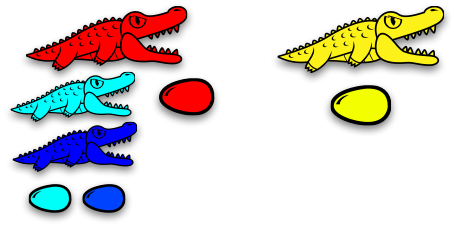
На картинке выше зелёный и красный цвета имеются в первой и второй семье. Поэтому во второй семье оба этих цвета необходимо заменить. Пусть, к примеру, зелёный будет заменён на голубой, а красный на синий.
Теперь, когда нет совпадений цветов, можно продолжить пожирание!
И далее!
И ещё далее!
И опять, пока не останется ничего, что можно было бы скушать.
Старые аллигаторы[править | править код]
Имеется ещё одно правило в этой игре, и оно касается старых аллигаторов:
На этой картинке самый верхний левый аллигатор не голоден. Он не собирается что-либо пожрать. Всё, что он делает, так это охраняет свою семью. Когда он умрёт?
Он умрёт тогда, когда он будет охранять только одну вещь. Как раз сейчас он охраняет две семьи — зелёную и красную. Обе нуждаются в том, чтобы о них кто-то заботился. Но зелёный аллигатор голоден. Поэтому он съедает красную семью…
Теперь старый аллигатор охраняет только одну семью. Эта семья может сама о себе позаботиться. Старый аллигатор больше н нужен, поэтому он состаривается и умирает.
Это правило старения. Если старый аллигатор охраняет только одну вещь, он умирает.
Теперь красный аллигатор пожирает жёлтую семью, и не остаётся ничего, что можно было бы скушать.
Игра[править | править код]
Игра состоит из серии задачек, которые заставляют игрока скармливать аллигаторам нечто, чтобы получить что-то новое. Например:
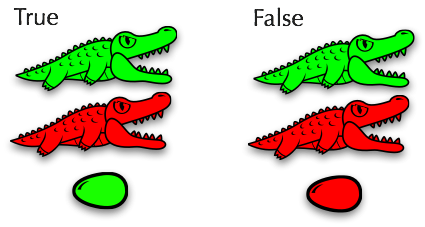
Вот две семьи. Они называются «True» и «False»:
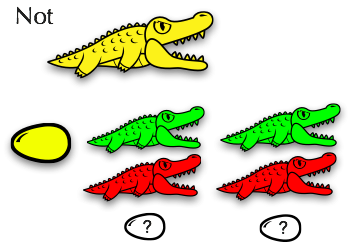
А вот семья, которая называется «Not»:
Когда «Not» пожирает «True», она оставляет после себя «False». А когда «Not» пожирает «False», она оставляет после себя «True». Какими цветами должны быть раскрашены два яйца в самом низу семьи «Not»?
Для того, чтобы решить эту задачу успешно, нам надо улучшить правило замены цветов, чтобы оно гласило, что семьи разных цветов, но одинаковой конфигурации эквивалентны.
Эти задачки можно объединять в рассказы. Игрок должен будет решить каждую задачку для того, чтобы увидеть, что произойдёт далее. В альтернативном варианте всё это можно сделать в виде настольной игры. Каждый игрок бросает кость, ходит на несколько шагов и решает задачку на поле, на которое попал.
Теория[править | править код]
Эта игра представляет собой нетипизированное λ-исчисление. Голодный аллигатор соответствует λ-абстракции, старый аллигатор представляет собой скобки, а яйца же являются связанными переменными. Правило пожирания соответствует β-редукции. Правило замены цветов соответствует α-конверсии. Правило старения говорит о том, что если что-то одно осталось в скобках, то скобки можно опустить.
Варианты[править | править код]
Оливер Стил указал, что роль семьи в жизни ребёнка очень велика, и можно было бы найти применение понятиям дедушек и бабушек, родителей, детей (яиц) и т. д. На текущий момент имена переменных представляются цветами. И то, и другое назначаются произвольно, а потому требуют правило замены имён/цветов для избежания коллизий. В качестве альтернативы можно использовать что-то вроде индексов де Брюйна, что может соответствовать порядку рождения в семье.
Оливер также указал, что детям может не понравиться идея о том, что родители умирают, а потому убирание аллигатора может быть объяснено тем, что он ушёл.
Изменяя игру таким образом, что аллигаторы голодны, а потому кушают всё, что находится перед ними, мы показываем правоассоциативное λ-исчисление. Это помогает убрать множество лишних скобок (старых аллигаторов) в нумералах Чёрча, комбинаторе неподвижной точки Y и т. д. К сожалению, среди прочих проблем это предполагает и то, что старый аллигатор должен нарождаться, если голодный аллигатор съел больше, чем одну вещь. Я ещё буду думать над тем, как сделать так, чтобы нумералы Чёрча (повторяющиеся применения) выглядели бы менее уродливо.
Схематичная форма[править | править код]
Я нашёл, что схематичная форма «исчисления аллигаторов» весьма помогает вручную вычислять λ-термы. Мы рисуем λ-абстракцию в виде линии с открытым ртом. Скобки обозначаются простой линией. Вот, к примеру, функция тождества:
Вот несколько нумералов Чёрча:
Вот булевские функции конъюнкции и дизъюнкции (предполагающие стандартные определения значений истинности):
Комбинатор Y:
Я не знаю, легче ли читать такую запись, нежели стандартную нотацию, но я обнаружил, что с такой записью удобней работать при использовании карандаша и бумаги. Я представляю λ-термы пожирающими друг друга и вылупляющимися из яиц. Я не теряюсь в неимоверных цепочках символов, теряя след того, что происходит и что применяется к чему.