 где С ' (х)=dС(х)/dx, D ' (p)=dD(p)/dp.
где С ' (х)=dС(х)/dx, D ' (p)=dD(p)/dp. Математическая модель экономики посредников
Экономическая ситуация в России вышла за рамки всех исторических аналогов и всех моделей, описанных в литературе. История не знает прецедентов, когда рабочим месяцами не выплачивают зарплату, доля бартера в расчетах между предприятиями превзошла 50 процентов, возрастает объем неплатежей между предприятиями, не выплачиваются налоги в федеральный и местные бюджеты. Дошло до того, что одна крупная фирма заплатила налоги в бюджет одного из регионов пачками чая по 150 рублей штука, и пластмассовыми табличками по 6000 рублей. Надпись на табличках гласила: "ВЫХОДА НЕТ". Перед экономической наукой встала задача по объяснению описанных парадоксов.
Условно можно выделить две научные школы, имеющих совершенно различный взгляд на причины сложившейся ситуации. Первую из них можно назвать школой технологической неэффективности. К ней относятся такие ученые, как Е. Гайдар, А. Илларионов, Б. Икес, Р. Фридман, А. Рападзински, Дж. Эрли. Они считают, что в экономике много технологически отсталых фирм, себестоимость продукции которых выше, чем ее рыночная цена. В таких условиях любая западная фирма разорилась бы в короткий срок. Но у российских предприятий есть два запасных выхода: они могут добиваться субсидий, или хотя бы фактического права не платить налоги, шантажируя правительство угрозой увольнения большого количества работников. Второй выход заключается в том, что предприятие завышает цену на свою продукцию, и ищет другое предприятие, которое готово поменять по бартеру свою также нерентабельную продукцию. Так в экономике возникают бартерные цепочки. Когда у кого-либо из участников цепочки возникает необходимость в живых деньгах, он вынужден продать полученную по бартеру продукцию по реальной рыночной цене, что приводит к крупным убыткам, которые предприятие перекладывает на своих контрагентов в виде неплатежей. Эту точку зрения представляла недавно опубликованная в журнале модель Гадди и Икеса. Выход из ситуации видится достаточно простым: необходимо обанкротить все нерентабельные предприятия (больше половины российской промышленности), привлечь иностранные инвестиции и на обновленной технической базе построить новую промышленность. В этом рецепте существует, правда, существенный изъян: ни один нормальный инвестор не станет вкладывать деньги в страну, где около половины населения не имеют работы и средств к пропитанию.
Другую школу можно условно назвать школой институциональной неэффективности. К ней можно отнести таких ученых, как Д. Львов, С. Глазьев, А. Некипелов, Г. Шмелев, А. Белоусов и др. Представители этой школы считают, что, хотя технологическая база российской экономики действительно устарела, чрезвычайно низкая цена труда позволила бы ей быть достаточно прибыльной, если бы не определенные институциональные особенности сложившейся экономической системы. Полученная прибыль могла бы стать основой собственных средств, инвестируемых в развитие производства – основного источника инвестиций во всем мире. Однако, результатом проведенной приватизации стала такая ситуация, когда высший менеджмент не является хозяином предприятий, но осуществляет никем не контролируемое оперативное управление собственностью. Совершенно естественно в таком случае желание менеджмента "приватизировать" текущий доход от деятельности предприятия, направив финансовые потоки через подконтрольные структуры. Из-за нежелания, чтобы живые деньги уходили из рук менеджмента, в качестве платежных средств активно используются бартер, квазиденьги и неплатежи. Поэтому для возрождения экономики необходимо сначала провести не технологическую, а институциональную реструктуризацию, в основе которой должна лежать коренная реформа отношений прав собственности. Только после этого можно будет найти внутренние источники инвестиций для технического перевооружения промышленности.
Безусловно, в реальной российской экономике одновременно присутствуют как элементы технологической, так и институциональной неэффективности. Однако, необходимо выяснить вопрос о том, какие элементы являются доминирующими и определяют генеральное направление развития экономики, а какие второстепенны и лишь дополняют картину. Представленные в статье статическая и динамическая модели экономики, созданные на базе взглядов экономистов школы институциональной неэффективности, показывают, что их подход позволяет объяснить многие парадоксальные явления российской действительности от кризиса неплатежей до системного кризиса, разразившегося после 17 августа.
В статической модели рассматривается такой интересный феномен, как возникновение в экономике нового типа посредников, редко встречающихся в рыночных экономиках. Эти посредники навязывают предприятиям невыгодные условия поставок сырья и сбыта продукции и обогащаются фактически за счет безвозмездного присвоения амортизационных, налоговых отчислений и отчислений на оплату труда. Основное отличие этого типа посредников от классических заключается в том, что нормы прибыли посредников и предприятий не имеют тенденции к выравниванию. Это наглядно видно из того, что посредники вывозят за границу капитал в больших количествах, тогда как предприятия не имеют денег на выплату зарплаты.
Построенная модель описывает такие особенности российской экономики, как высокий уровень налоговых ставок, низкая собираемость налогов, высокая степень криминализации экономики, существование посредников, паразитирующих на предприятиях, и кризис неплатежей.
Модель создана на основе следующих предпосылок:
Таким образом, получена задача: max(aPl+(1-a)Pn), где Pl=tl (pl ( D(pl)–xt )+ptxt) – C(D(pl)), Pn=tcxt (pc-pt) при ограничениях: 0 Ј pt, pt Ј pc, pc Ј pl, D(pl) і xt. Предположим, что С(х) и D(p) дважды дифференцируемы, тогда, решив поставленную задачу стандартным методом Лагранжа максимизации функции нескольких переменных при наличии ограничений, получим:
 где С ' (х)=dС(х)/dx, D ' (p)=dD(p)/dp.
где С ' (х)=dС(х)/dx, D ' (p)=dD(p)/dp.
Таким образом, если доля выручки, оставляемая предприятию государством, с учетом значимости этой доли выручки для менеджмента предприятия (atl), будет меньше доли выручки, оставляемой криминальными структурами посреднику, с учетом значимости этой доли выручки для менеджмента ((1-a)tc), то предприятие всю торговлю будет осуществлять через посредника, в противном случае вся торговля будет осуществлятся предприятием самостоятельно. На взгляд автора, в этом и заключается инициирующий механизм кризиса неплатежей: поскольку предприятия, торгующие через посредников, не получают выручки, но имеют затраты на производство продукции, то они перекладывают свою задолженность на своих контрагентов. В свою очередь, контрагенты вынуждены перекладывать эту задолженность дальше, разворачивая цепочку неплатежей.
Для получения решения уравнений в явном виде, подставим в них простейшие функции спроса и предложения в виде: D(p)=max(d0-d1p,0), C(x)=c1x. Мы получим:
Тогда величина сбора легальных налогов составит:
Tl(a)=(1-tl)ql(a) pl(a),

Объем нелегальных налогов будет равен:
Tc(a)=(1-tc)qc(a) pc(a),
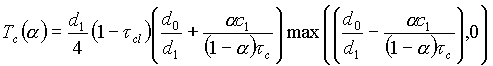
Следует отметить тот факт, что в приведенной модели предприятие платит налоги либо только государству, либо только криминальным структурам. По всей видимости, это объясняется тем, что функция полезности менеджмента предприятия моделируется линейной комбинацией прибыли предприятия и посредника. В реальности это условие, вероятно, не соблюдается, поэтому часть деятельности предприятия осуществляется легально, а часть – нелегально. Введение нелинейной функции полезности усложнило бы математические выкладки, не приведя к принципиально новым результатом, поэтому в рамках данной модели факт сбора налогов как криминальными структурами, так и государством объясняется различием в значении параметра a у менеджмента различных предприятий. Те предприятия, у менеджмента которых aіtс/(tс+tl), платят налоги государству, а те, у которых a<tс/(tс+tl), платят налоги криминальным структурам.
Теперь вычислим суммарный сбор налогов со всех предприятий. Для этого необходимо подобрать плотность распределения a dW(a) на интервале от 0 до 1. К сожалению, оценка реальных вида распределения a и параметров этого распределения невозможна, в виду отсутствия статистических данных. В рамках данной модели в целях упрощения можно предположить, что все предприятия имеют одинаковые параметры c1, d0 и d1. В качестве плотности распределения dW(a) возьмем функцию вида:

В формуле введено обозначение: g - параметр, характеризующий среднюю заинтересованность менеджмента в прибыли своих предприятий a a n и связанный с ней соотношениями:
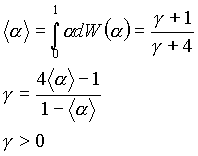
Введенная таким образом плотность распределения a непрерывно дифференцируема на интервале (0;1) и стремится к 0 на его границах, что соответствует интуитивным предпосылкам Она позволяет варьировать степень средней заинтересованности менеджмента предприятий в результатах их деятельности, и удобна для интегрирования.
После выбора плотности распределения a можно получить значения суммарного сбора налогов государством, криминальными структурами, суммарных объемов производства в легальном секторе экономики, суммарных объемов производства в теневом секторе экономики, суммарных прибылей предприятий легального сектора, суммарных прибылей посредников и суммарных убытков предприятий, торгующих через посредников (что в рамках данной модели трактуется как объем неплатежей в экономике. Также можно рассчитать средние уровени цен в легальном секторе, теневом секторе и в целом по экономике. Однако формулы получаются чрезвычайно громоздкими, поэтому ниже будут приведены их графики. Если вы хотите просмотреть полученные формулы, нажмите здесь.
Вычислив в явном виде вышеназванные величины, можно приступить к исследованию модели. Исходная гипотеза заключается в том, что коррумпированный бюрократический аппарат сросся с криминальными структурами, поэтому бюрократы непосредственно устанавливают такой уровень теневых налоговых ставок и лоббируют установление такого уровня официальных налоговых ставок, чтобы максимизировать свою целевую функцию вида bTl+(1-b)Tс, где параметр b характеризует степень заинтересованности бюрократического аппарата в пополнении бюджета. С формальной точки зрения, необходимо найти максимум этой функции по параметрам tl и tc. Поскольку затруднительно найти аналитическое выражение для tl и tc, соответствующих максимуму целевой функции бюрократического аппарата, в представленной модели он ищется численно.
Полученные в модели формулы громоздки
и сложны для анализа, поэтому представим их
графики. 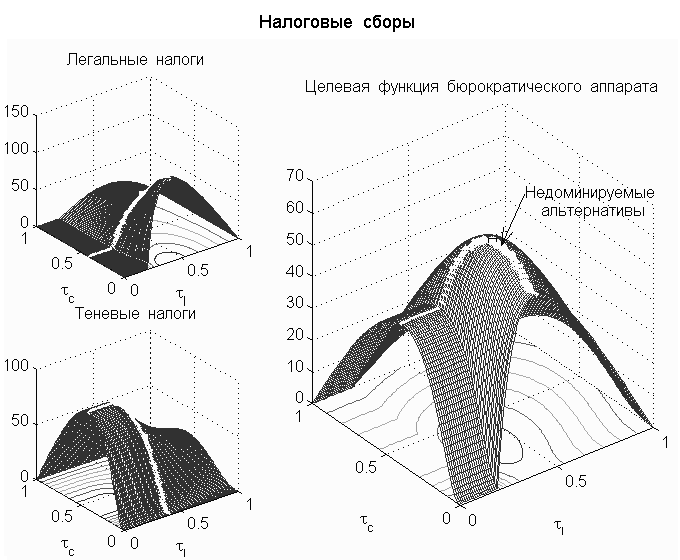 На рисунке 1
изображены поверхности Лаффера,
характеризующие зависимость сбора налогов от
значений ставок легальных и теневых налогов,
отложенных в горизонтальной плоскости. На левом
верхнем рисунке изображена кривая зависимости
легальных налоговых сборов от доли дохода,
оставляемого в распоряжении фирмы легальными и
нелегальными структурами (tl
и tc соответственно). При
каждой фиксированной величине tс
мы получаем известную в макроэкономике кривую
Лаффера: по мере увеличения ставки налога
(уменьшения tl) налоговые
сборы сначала растут, а затем начинают падать
из-за ухода в теневой сектор и свертывания
производства. При величине tl<c1d1/d0
легальное производство полностью прекращается,
так как производители вынуждены устанавливать
такие цены, что спрос на их продукцию падает до 0.
При меньшей величине нелегального
налогообложения (большей величине tс)
высота соответствующей кривой Лаффера ниже:
большее количество предприятий уходят в теневой
сектор из-за возрастания выгодности
правонарушений. Поэтому при каждой
фиксированной величине tl по
мере возрастания tс
собираемость налогов снижается. Левый нижний
рисунок отражает ситуацию со сбором нелегальных
теневых налогов, которая является инверсной по
отношению к ситуации в легальном секторе: при
фиксированной легальной ставке налога
наблюдается эффект Лаффера в зависимости от
значения нелегальной ставки, а при уменьшении
налогообложения в легальном секторе и
сохранении нелегальной ставки на том же уровне,
собираемость нелегальных налогов падает. На
правом рисунке изображена целевая функция
бюрократического аппарата, которая в данной
модели в целях упрощения представляет линейную
комбинацию легальных и нелегальных сборов,
взвешенных с весами b и 1-b
соответственно. Белыми полосами отмечено
множество недоминируемых альтернатив между
сбором легальных и теневых налогов. Оно
представляет множество таких комбинаций
налоговых ставок, для каждой из которых
невозможно увеличить собираемость одного из
видов налогов, не уменьшив собираемости другого.
При принятии решения о установлении налоговых
ставок рационально действующий аппарат будет
принимать во внимание только альтернативы из
этого множества.
На рисунке 1
изображены поверхности Лаффера,
характеризующие зависимость сбора налогов от
значений ставок легальных и теневых налогов,
отложенных в горизонтальной плоскости. На левом
верхнем рисунке изображена кривая зависимости
легальных налоговых сборов от доли дохода,
оставляемого в распоряжении фирмы легальными и
нелегальными структурами (tl
и tc соответственно). При
каждой фиксированной величине tс
мы получаем известную в макроэкономике кривую
Лаффера: по мере увеличения ставки налога
(уменьшения tl) налоговые
сборы сначала растут, а затем начинают падать
из-за ухода в теневой сектор и свертывания
производства. При величине tl<c1d1/d0
легальное производство полностью прекращается,
так как производители вынуждены устанавливать
такие цены, что спрос на их продукцию падает до 0.
При меньшей величине нелегального
налогообложения (большей величине tс)
высота соответствующей кривой Лаффера ниже:
большее количество предприятий уходят в теневой
сектор из-за возрастания выгодности
правонарушений. Поэтому при каждой
фиксированной величине tl по
мере возрастания tс
собираемость налогов снижается. Левый нижний
рисунок отражает ситуацию со сбором нелегальных
теневых налогов, которая является инверсной по
отношению к ситуации в легальном секторе: при
фиксированной легальной ставке налога
наблюдается эффект Лаффера в зависимости от
значения нелегальной ставки, а при уменьшении
налогообложения в легальном секторе и
сохранении нелегальной ставки на том же уровне,
собираемость нелегальных налогов падает. На
правом рисунке изображена целевая функция
бюрократического аппарата, которая в данной
модели в целях упрощения представляет линейную
комбинацию легальных и нелегальных сборов,
взвешенных с весами b и 1-b
соответственно. Белыми полосами отмечено
множество недоминируемых альтернатив между
сбором легальных и теневых налогов. Оно
представляет множество таких комбинаций
налоговых ставок, для каждой из которых
невозможно увеличить собираемость одного из
видов налогов, не уменьшив собираемости другого.
При принятии решения о установлении налоговых
ставок рационально действующий аппарат будет
принимать во внимание только альтернативы из
этого множества. 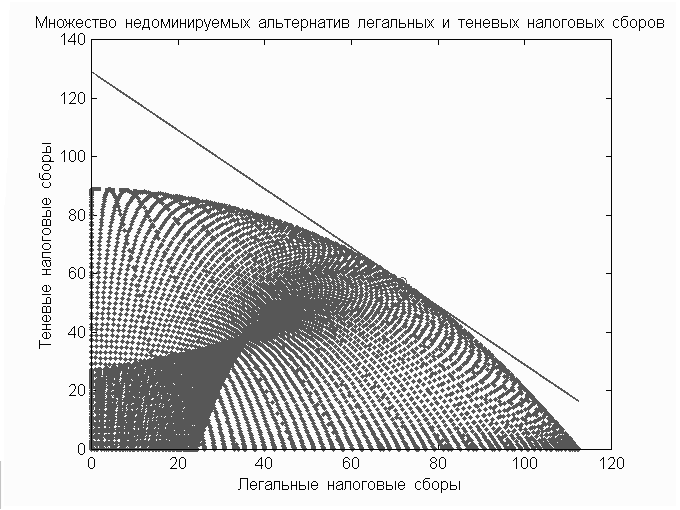 На
рисунке 1а изображено множество всех возможных
значений налоговых сборов, его внешняя граница,
являющаяся множеством недоминируемых
альтернатив, и наивысшая из достижимых линий
уровня функции полезности чиновничьего
аппарата. Точка пересечения этой линии уровня
(являющейся в данной модели прямой линией) с
множеством недоминируемых альтернатив,
отмеченная на всех рисунках в виде белого
квадратика, является решением задачи. Наклон
прямой определяется коэффициентом b
и характеризует степень заинтересованности
чиновничьего аппарата в сборе легальных налогов
по сравнению со сбором теневых налогов.
На
рисунке 1а изображено множество всех возможных
значений налоговых сборов, его внешняя граница,
являющаяся множеством недоминируемых
альтернатив, и наивысшая из достижимых линий
уровня функции полезности чиновничьего
аппарата. Точка пересечения этой линии уровня
(являющейся в данной модели прямой линией) с
множеством недоминируемых альтернатив,
отмеченная на всех рисунках в виде белого
квадратика, является решением задачи. Наклон
прямой определяется коэффициентом b
и характеризует степень заинтересованности
чиновничьего аппарата в сборе легальных налогов
по сравнению со сбором теневых налогов.

На рисунке 2 изображены объемы легального, теневого производства и общий объем производства в зависимости от уровня легальных и теневых налоговых ставок. На этих рисунках видно, что при возрастании налоговых ставок объем производства падает, причем при возрастании легальных налоговых ставок производство частично перетекает в теневой сектор, и наоборот. Это соответствует реальной ситуации, когда чрезмерное налогообложение законопослушных производителей душит производство. Интересно отметить, что даже при нулевом уровне легальных налоговых ставок существует теневое производство. Этот факт демонстрирует недостаточность снижения легальных налогов для борьбы с теневым сектором. Необходимо проводить комплексную политику, заключающуюся в снижении легальных налоговых ставок и одновременном увеличении трансакционных издержек нахождения в теневом секторе. В рамках данной модели это будет интерпретироваться как одновременное увеличение tl и снижение tc, однако в этом случае изымаемая часть криминальной прибыли пойдет не на увеличение доходов коррумпированных бюрократов, а на предварительную моральную компенсацию риска поимки для правонарушителя.

На рисунке 3 изображены средние уровни цен. Верхний левый рисунок демонстрирует зависимость среднего уровня цен в легальном секторе от налоговых ставок. При значении tl=c1d1/d0 цены достигают того уровня, когда спрос в легальном становится равным 0, поэтому автор принял, что при дальнейшем повышении налогов цены остаются на этом уровне. На нижнем левом рисунке изображены средние цены в теневом секторе, а на правом – общий уровень цен. Мы можем видеть, что увеличение налогообложения существенным образом способствует взвинчиванию цен, из-за чего страдают потребители. Полученные результаты соответствуют заявлениям о том, что в российской экономике цены на многие товары существенно завышены.
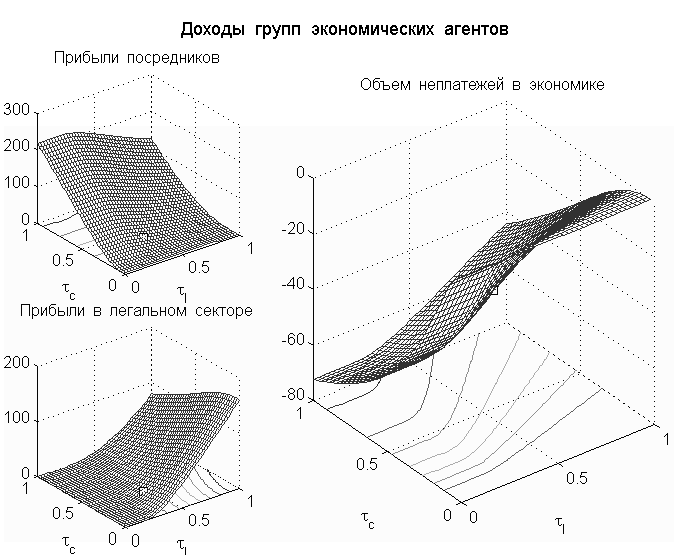
На рисунке 4 построены поверхности, изображающие прибыли легальных производителей, посредников и убытки предприятий, торгующих через посредников. На левом нижнем рисунке видно, что прибыли предприятий легального сектора возрастают по мере сокращения легального и теневого налогообложения. Левый верхний рисунок, напротив, показывает, что при сокращении легального налогообложения прибыли посредников падают, а при сокращении теневого налогообложения – растут. На правом рисунке изображен объем неплатежей, который возрастает как при увеличении легальных, так и теневых налогов. Как уже было отмечено выше, даже при нулевом уровне легального налогообложения часть продукции реализуется в теневом секторе, что приводит к положительным прибылям посредников и проблеме неплатежей.
Все графики построены для следующих значений параметров: c1=2, d0=100, d1=10, b =0,5, g =2, a a n =1/2. Качественно вид графиков не зависит от значений параметров, хотя количественные характеристики и подвержены изменению.
Автором был проведенный анализ чувствительности величины сбора налогов в модели в зависимости от изменения степени заинтересованности в добросовестном исполнении своих обязанностей менеджмента предприятий, бюрократов, изменения издержек и изменения степени монополизированности экономики. Анализ был проведен путем варьирования коэффициентов g , b , c1 и отношения d0/d1. Результаты анализа показали, что, в зависимости от степени монополизированности экономики, наиболее эффективной мерой повышения собираемости налогов является либо увеличение степени ее монополизированности (при изначально низком уровне монополизированности), либо увеличение степени заинтересованности бюрократов в добросовестном исполнении своих обязанностей. Действительно, правительство Е. М. Примакова в качестве одной из главных мер пополнения бюджета называет введение государственной монополии на алкогольную продукцию, также в качестве одной из необходимых мер называется снижение уровня налогов. В рамках данной модели это можно интерпретировать как существенное увеличение степени "честности" членов нового правительства по сравнению с предыдущими. Увеличение степени заинтересованности менеджмента в прибыли своих предприятий по степени эффективности является следующей мерой после увеличения степени заинтересованности бюрократов в сборе налогов. Самой малоэффективной мерой является снижение издержек. Это находит подтверждение в действительности: снижение железнодорожных тарифов не привело к сколько-нибудь заметному оживлению производства и увеличению сбора налогов.
Представленная модель позволяет заключить, что одними из основных направлений по выводу экономики из кризиса могли бы стать:
Предложенная модель является статической и ничего не говорит нам о развитии процесса во времени. Покажем, как с помощью простейших дифференциальных уравнений можно построить модель, достаточно адекватно описывающую многие динамические особенности российской экономики.
Динамическая математическая модель
Рассмотрим замкнутую экономику с фиксированными производственными мощностями. В такой экономике производится один вид благ, используемых на потребление населения и в качестве сырья и полуфабрикатов для производства. Для упрощения картины, будем рассматривать ВВП в постоянных ценах. Пусть сначала существует недогрузка мощностей, тогда любое приращение выпуска будет приводить как к росту доходов в экономике, так и к росту предложения сырья и полуфабрикатов. Рост доходов будет приводить к увеличению совокупного спроса, а рост предложения сырья и полуфабрикатов предоставит возможности удовлетворить растущий спрос путем дальнейшего увеличения выпуска. Таким образом, экономика будет расти благодаря действию эффекта мультипликатора. По мере сокращения объема свободных мощностей и уменьшения величины мультипликатора, темп роста экономики будет сокращаться, пока не станет равным нулю при достижении полной загрузки. При дальнейшем увеличении производства, темп роста станет отрицательным из-за возникновения дефицитов сырья и поломок оборудования, работающего с перегрузкой. Математически это можно представить в виде дифференциального уравнения первого порядка: dY/dt=f(Y), где Y – ВВП в постоянных ценах, f(Y) - скорость роста ВВП. f(Y)>0 , при 0<Y<Ymax; f(Y)=0 , при Y=0 и Y=Ymax; f(Y)<0 , при Y>Ymax, где Ymax - ВВП, соответствующий уровню оптимальной загрузки производственных мощностей. Исходя из общих соображений, очевидно, что f(Y) – непрерывная гладкая функция. Предположим, что она имеет единственный максимум. Простейшее математическое выражение такой функции, обладающее всеми названными свойствами – две параболы, одна из которых выходит из начала координат, а другая из точки (Ymax, 0). Они склеиваются в точке максимальной скорости роста, причем эта точка является вершиной каждой из них. Рисунок 5 демонстрирует поведение ВВП с течением времени в зависимости от начального уровня ВВП. В системе существует два стабильных состояния, соответствующих 0 и Ymax. Из любого начального состояния система притягивается к состоянию с уровнем ВВП, равным Ymax, достигая его формально за бесконечное время. Таким образом, это состояние является устойчивым. Состояние, соответствующее нулевому ВВП, не является устойчивым, и малейшее случайное отклонение от него приводит к дальнейшему возрастанию ВВП вплоть до уровня Ymax.
Таким образом, в замкнутой экономике с фиксированными производственными мощностями, устанавливается устойчивое равновесие, соответствующее оптимальной загрузке имеющихся мощностей. Инвестиции в производство в такой экономике приводят к росту Ymax и, соответственно, к смещению положения равновесия.

Усложним модель, рассмотрев открытую экономику, где экономическая элита (посредники, коррумпированные менеджеры и бюрократы) максимизирует свои доходы, которые получает путем изъятия части прироста ВВП. Примем, что "аппетиты" элиты линейно растут по мере роста ВВП по закону: a+bY. Уравнение изменения ВВП имеет вид: dY/dt=f(Y)-(a+bY). a характеризует “жадность” элиты: она показывает, какую долю прироста элита изымает независимо от состояния дел в экономике. Очевидно, a тем выше, чем большее значение для элиты имеет эффект демонстративного потребления, и чем менее она уверена в своем будущем. Доходы, полученные элитой вывозятся за границу. Поэтому эти доходы представляют собой чистый вычет из ВВП.
Условие максимизации доходов элиты на протяжении достаточно длительного временного интервала приводит к подбору коэффициента d таким образом, чтобы график их доходов пересекал график прироста ВВП в точке максимума последнего.
В предложенной модели существует три положения равновесия: Y*1, Y*2 и 0. Если система в начальный момент находилась в точке выше Y*1, она с течением времени притягивается к состоянию Y*2 и достигает его формально за бесконечное время. Если система находится в положении ниже Y*1, то она падает до нуля за конечное время, то есть реально очень быстро. Таким образом, Y*2 и 0 являются устойчивыми состояниями, а Y*1 - неустойчивым. На рисунке 6 изображено поведение такой системы.
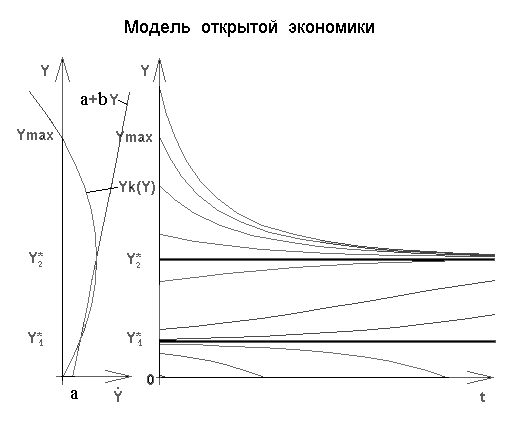
Мы получили, что, если в начальный момент времени система находится в положении, соответствующем оптимальной загрузке производственных мощностей, с течением времени ВВП сокращается до уровня, при котором отток средств из экономики максимален. В таком случае осуществление инвестиций в экономику нерационально, так как и существующие мощности не используются в полном объеме.
Прогноз на основе динамической модели
Несмотря на чрезвычайную простоту, предложенная динамическая модель интересна своими прогностическими возможностями. Из нее вытекает, что система абсолютно устойчива к возрастанию ВВП: любой случайный рост экономики, вызванный факторами, неучитываемыми в данной модели, со временем гасится системой за счет возрастания оттока капитала. Это подтверждается опытом последних лет, когда все положительные тенденции в экономике со временем затухали. Среднесрочное развитие экономики, согласно модели, характеризуется колебаниями ВВП около уровня Y*2, а долгосрочное – понижающимся трендом из-за снижения Y*2 под воздействием износа производственных мощностей. При этом будут медленно снижаться доходы экономической элиты за счет снижения максимальной скорости роста ВВП.
С другой стороны, система обладает только ограниченной способностью гасить сокращения ВВП: если ВВП упадет до уровня ниже Y*1, то ВВП будет падать со все возрастающей скоростью до нулевого значения, что означает полный крах экономики. При этом чем в меньшей степени элита согласует свои потребности с состоянием экономики, то есть чем больше параметр а, тем меньше расстояние между Y*2 и Y*1, и тем меньше устойчивость системы. Ситуация осложняется еще и тем, что в случае начала нового спада экономики, экономическая элита может потерять уверенность в будущем и резко увеличить отток капитала из экономики.
Одним из главных внешних по отношению к данной модели факторов падения ВВП, является сокращение мировых цен на основные товары российского экспорта – энергоносители, что привело к сокращению объема ВВП в долларовом выражении, и побудило элиту увеличить отток капитала в реальном выражении для сохранения своих валютных доходов на прежнем уровне.
Падение мировых цен на нефть поставило российскую экономику на грань краха и, вследствие падения экспортных доходов, привело к дефолту 17 августа. Сделанные в начале октября нефтяными компаниями заявления о том, что они не будут поставлять в страну экспортную выручку, можно интерпретировать как желание экономической элиты увеличить долю изъятий из ВВП из-за уменьшения ее доходов и угрозы нестабильности в стране. Хочется надеяться на то, что приход к власти правительства Е. М. Примакова будет означать катастрофу сложившейся паразитической системы, то есть кардинальное изменение системы взаимосвязей между экономическими субъектами, но не катастрофу экономики России.
Заключение
В статье рассмотрены принципиальные черты экономики, в которой доминирующими экономическими агентами являются посреднические фирмы, сросшиеся с коррумпированной частью бюрократического аппарата. Представленные математические модели описывают многие характерные особенности российской экономики в статическом и динамическом аспектах и подтверждается реальными фактами экономической действительности. Они также может быть успешно использованы для качественного сравнения различных вариантов экономической политики и выработки практических рекомендаций для органов государственной власти. Часть предложений, вытекающих из анализа представленной статической модели, уже входят в экономическую программу нового правительства. Автору представляется, что поднятая тема заслуживает дальнейшего обсуждения.
Библиография
Назад к тексту
Введем обозначения:

Теперь можно получить значения суммарного сбора налогов государством:
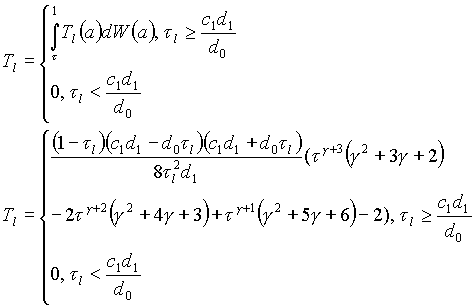
криминальными структурами:
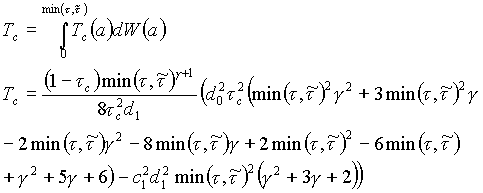
суммарных объемов производства в легальном секторе экономики:

суммарных объемов производства в теневом секторе экономики:

суммарных прибылей предприятий легального сектора:
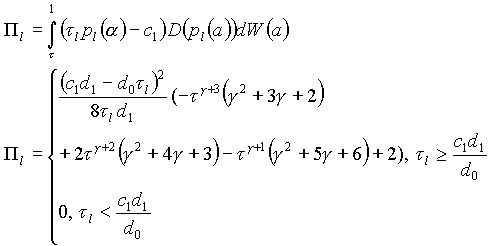
суммарных прибылей посредников:
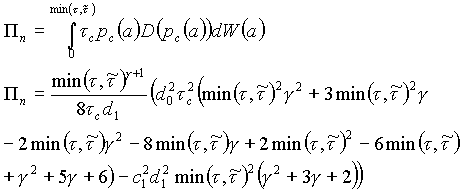
и суммарных убытков предприятий, торгующих через посредников, что в рамках данной модели трактуется как объем неплатежей в экономике:

Средний уровень цен в экономике составит:
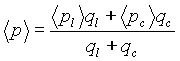
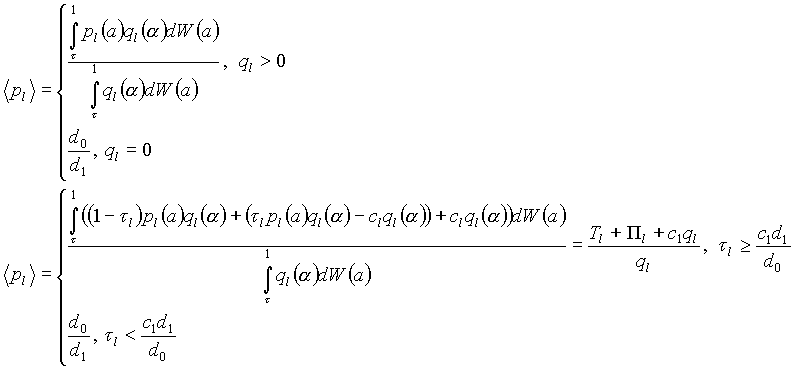
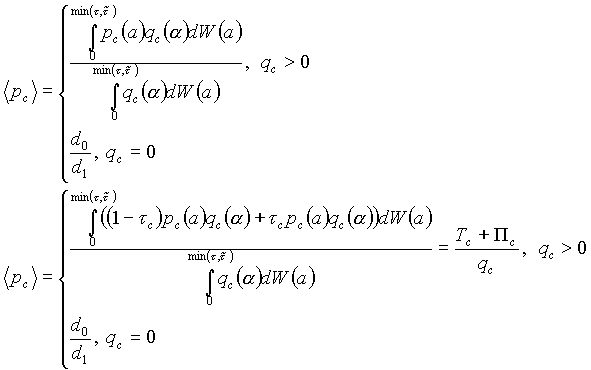
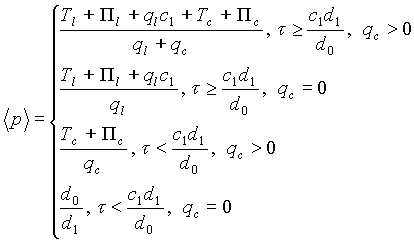
Взятие минимума в формулах обусловлено наличием излома функции спроса, связанного с неотрицательностью ее значений.
Назад к тексту
/ /\ \