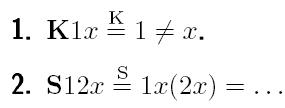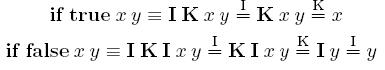Текст:Роман Душкин:Комбинаторы? Это просто!
- Исходный вариант статьи (Р. В. Душкин, «Комбинаторы? - Это просто!») опубликован в журнале «Потенциал», №7, 2006.
Данная статья описывает основы комбинаторной логики - математической науки о вычислениях, в которой любые объекты изучения выражаются при помощи двух базовых объектов S и K, называемых комбинаторами, и одной операции над ними - операции применения одного комбинатора к другому.
Введение[править | править код]
Комбинаторная логика (от слова «комбинатор», а не «комбинаторика»)— это направление в математической логике, разработанное в первой половине XX века логиками Мозесом Шёнфинкелем и Хаскеллом Карри в качестве науки о вычислительных процессах. Хотя первоначально этот вид логики претендовал только на то, чтобы удалить из логических высказываний переменные, через некоторое время в информатике были получены прикладные результаты, показавшие, что комбинаторную логику можно использовать для проведения вычислений.
На комбинаторную логику можно смотреть как на некоторое упрощение -исчисления [1], в котором нет символа , а все функциональные абстракции представлены ограниченным набором символов, называемых «комбинаторами». Такие комбинаторы не содержат переменных, являются функциями высшего порядка, т.е. в качестве аргументов могут принимать на вход другие функции, а также описывают определённые правила преобразования объектов, поданных им на вход в качестве аргументов.
Другими словами, комбинаторная логика — это формализм для представления функциональных зависимостей между входными и выходными данными. В этом формализме зависимости и сами данные записываются в одном и том же весьма ограниченном алфавите.
Формальная теория[править | править код]
Для того, чтобы не быть голословным, необходимо чётко описать базовые объекты комбинаторной логики, которые участвуют в формальной системе, определяющей саму комбинаторную логику. Согласно математической практике, необходимо определить следующие элементы формальной системы:
- Алфавит.
- Утверждения (множество правильно построенных формул).
- Аксиомы.
- Правила вывода.
Под алфавитом понимается набор символов, допустимых в нотации
записей термов в комбинаторной логике. В общем виде при помощи
нотации комбинаторной логики можно записывать объекты нескольких
типов — константы, переменные, термы и специальные знаки.
Константы обозначаются малыми буквами латинского алфавита, возможно с индексами. Обычно для обозначения констант берутся символы с начала алфавита. Переменные обозначаются также малыми буквами, возможно, с индексами, но при этом они обычно выбираются с конца алфавита: , — константы, , — переменные.
Однако для выделения константных объектов иногда будет использоваться иной способ записи. Такой способ заключается в выделении наименований констант полужирным начертанием — эта запись будет использоваться, если наименование константы состоит более чем из одного символа: if, true, pair и др.
Комбинаторные термы (или просто «выражения») будут обозначаться
заглавными буквами латинского алфавита, возможно также с индексами:
, и т. д.
Из специальных символов в комбинаторной логике используется всего три: это скобки «(» и «)», а также знак равенства (). Последний обозначает отношение конвертируемости — возможность преобразования одного терма в другой. С точки зрения вычислительных процессов, отношение конвертируемости определяет сам процесс вычисления значения функции, представленной комбинаторным термом.
Множество правильно построенных формул в комбинаторной логике
выглядит очень просто. Его составляют выражения вида {},
где и — комбинаторные термы. При этом сами комбинаторные
термы строятся по индукции:
1) {если — константа, то — комбинаторный терм;}
2) {если — переменная, то — комбинаторный терм;}
3) {если и — комбинаторные термы, то — комбинаторный терм;}
4) {других комбинаторных термов нет.}
В этом индуктивном определении выражение обозначает операцию аппликации, единственную операцию комбинаторной логики. Аппликация описывает применение функции (в данном примере — терм ) к её аргументу или аргументам (в данном примере — терм ).
Как видно, создание комбинаторных термов повлечёт за собой
лавинообразное внедрение в запись таких термов скобок. Для того,
чтобы уменьшить количество скобок в записях комбинаторных термов,
вводятся соглашения о скобках, которые заключаются в том, что
пропущенные скобки восстанавливаются по ассоциативности влево:
В качестве аксиом, входящих в множество правильно построенных
формул, обычно выделяются следующие:
| Ix = x | (I) |
| Kxy = x | (K) |
| Sxyz = xz(yz) | (S) |
Данные аксиомы не надо доказывать, их наличие просто постулируется.
Эти аксиомы определяют три базовых комбинатора, использующихся для
вывода (вычислений) новых комбинаторов. Традиционно базис S,K,I
является тем набором первоначальных комбинаторов, через который
выражаются все прочие комбинаторы. Однако это не минимальный базис,
ибо наличие комбинатора I не обязательно в нём, т. к.
его можно выразить через комбинаторы S и K:
Другими словами, комбинаторный базис — это набор комбинаторов, через которые при помощи отношения конвертируемости () можно выразить все остальные комбинаторы. Минимальным комбинаторным базисом является набор из комбинаторов S и K, но обычно его дополняют комбинатором I для упрощения записи выражаемых комбинаторных термов. Однако разнообразных базисов может быть бесчисленное множество, и разные исследователи вводили разные базисы для своих целей. В следующем разделе будут рассмотрены некоторые примеры таких базисов.
Остаётся рассмотреть правила вывода, которые используются в рамках комбинаторной логики для преобразования одних термов в другие и описывают отношение конвертируемости (). Данные правила вывода по своей сути описывают это отношение, задавая его характеристики.
| a = a | {} |
| (a = b) (b = a) | {} |
| (a = b) (b = c) (a = c) | {} |
| (a = b) (ca = cb) | {} |
| (a = b) (ac = bc) | {} |
Как видно, первые три правила являются описанием свойств рефлексивности, симметричности и транзитивности. Набор этих свойств являет собой характеристики отношения эквивалентности, т. е. отношение конвертируемости () делит всё множество комбинаторных термов на некоторые классы эквивалентности, относительно которых можно сказать, что находящиеся в них термы конвертируемы друг в друга (эквивалентны друг другу).
Дополнительно надо отметить, что далее под именем комбинатора будет пониматься символ, его обозначающий, под сигнатурой комбинатора будет пониматься левая часть правила, а под характеристикой — правая часть правила, описывающего сам комбинатор.
Примеры сложных комбинаторов[править | править код]
Вполне естественно, что создатели комбинаторной логики не ограничились использованием двух базовых комбинаторов — S и K. Хотя они и составляют минимальный базис, но запись функций только через них увеличивает громоздкость определений с ростом сложности функций. Поэтому для упрощения записи определений более сложных комбинаторов и комбинаторных термов были разработаны дополнительные комбинаторы, из которых также можно составлять базисы.
К таким комбинаторам относятся следующие:
Данные комбинаторы весьма существенно сокращают некоторые преобразования [2] Ради этого многие комбинаторы даже получили свои собственные наименования. Так комбинатор I называется «комбинатором тождества», комбинатор K — «канцелятор», комбинатор S — «коннектор», комбинатор B — «композитор», комбинатор C — «пермутатор» и комбинатор W — «дубликатор».
Однако вполне понятно, что все перечисленные комбинаторы можно выразить друг через друга. Следующие формулы показывают выражение новых комбинаторов через уже известные:
Вдумчивому читателю предлагается самостоятельно проверить данные формулы. Для этого достаточно воспользоваться аксиомами для комбинаторов S и K и подставить в формулы переменные в заданном количестве (согласно определениям).
Однако возникает вопрос. На основании чего получены перечисленные выражения комбинаторов B, C и W через базисные? Как создать такие выражения самостоятельно? Можно попытаться ответить на этот вопрос, самостоятельно найдя выражение комбинатора I, как самого простого. Это можно проделать на основании следующих рассуждений.
Выражение комбинатора I может начинаться либо с комбинатора S, либо с комбинатора K. При помощи цифр в следующих записях будут обозначаться недостающие объекты, которые ещё необходимо найти. В этом случае два возможных пути поиска выражения для комбинатора I выглядят так:
Здесь видно, что первая альтернатива не подходит автоматически, т. к. канцелятор K отменяет переменную , которая должна появиться в самом конце. Соответственно далее надо рассматривать только вторую альтернативу и искать способ выражения неизвестных объектов и . Они также могут быть либо комбинатором S, либо комбинатором K. Соответственно, подставляя эти комбинаторы вместо неизвестного объекта , можно получить:
Как видно, первая альтернатива уже дала необходимый результат, а во второй альтернативе не хватает операндов у комбинатора S. Поэтому вторую альтернативу можно не рассматривать, а вернуться только к первой. В ней остаётся неизвестный объект , который не участвует в цепочке вывода, т. к. уничтожается канцелятором. Поэтому вместо него может стоять любой комбинатор, например, всё тот же K. Так и получается, что выражение комбинатора тождества таково:
Этот пример также показал, что способов разложения объектов в комбинаторном базисе существует бесконечное множество, поэтому всегда имеет смысл говорить о «минимальном» разложении, т. е. таком, в записи которого используется минимальное число комбинаторов и скобок.
Но описанный процесс не так прост, как может показаться на самом
деле. Достаточно попробовать разложить подобным образом относительно
простой комбинатор B, чтобы понять, что в процессе
такого рассмотрения альтернатив дерево решений растёт подобно
снежному кому. Поэтому ради облегчения процесса выражения объектов
с заданными комбинаторными характеристиками были созданы специальные
правила. Данные правила относятся к выражению в базисе S,K,I
- , где — переменная.
- .
- .
- , если .
- .
В этих правилах используется -нотация, которая принята в -исчислении. Привести комбинатор с его сигнатурой и характеристикой к -нотации довольно просто — надо вместо символа, обозначающего сам комбинатор, использовать символ (), а вместо символа () использовать точку ().
В следующем разделе приведены определения типов данных и функций на языке Haskell, которые осуществляют перевод заданного комбинатора в базис S,K,I. Однако для закрепления материала читателю предлагается самостоятельно выразить в базисе S,K,I следующие комбинаторы с такими характеристиками:
Модуль на языке Haskell для преобразования комбинаторов[править | править код]
В этом разделе приводится текст программы на языке Haskell, которая преобразует заданный комбинатор в базис S,K,I. Для того, чтобы понимать приведённые определения, необходимо быть знакомым с синтаксисом этого языка на уровне, достаточном для определения типов и функций. Рассмотрение этих тем выходит за рамки этой статьи, поэтому заинтересованного читателя можно отослать к специализированной литературе.
Для преобразования комбинаторов необходимо для начала определить тип данных для их представления. В соответствии с определением комбинаторного терма определение такого типа выглядит так:
data Combinator = Var String
| App Combinator Combinator
| Lam String Combinator
deriving Eq
Это определение полностью соответствует математическому, которое гласит, что комбинаторный терм — это либо переменная (Var — от английского слова «variable»), либо абстракция (Lam} — от английского слова «lambda»), либо приложение одного комбинаторного терма к другому (App — от английского слова «application»).
Для того, чтобы иметь возможность просматривать полученные результаты преобразования комбинаторных термов, необходимо определить тип Combinator экземпляром класса Show, который является классом величин, которые могут быть отображены. Конечно, интерпретатор языка Haskell может самостоятельно определить такой экземпляр, но он сделает это не так красиво, как можно сделать вручную. Поэтому вводится следующее определение:
instance Show Combinator where
show (Var x) = x
show (App x y) =
case y of
App _ _ -> showLam x ++ "(" ++ show y ++ ")"
_ -> showLam x ++ showLam y
where showLam l@(Lam _ _) = "(" ++ show l ++ ")"
showLam x = show x
show (Lam x e) = "\\" ++ x ++ "." ++ show e
Здесь видно, что переменная отображается просто своим именем,
которое представляется строкой символов. Применение комбинаторных
термов друг к другу просто записывается перечислением комбинаторных
термов друг за другом со взятием в скобки, если второй терм сложный.
А абстракция записывается при помощи символа () с
указанием сигнатуры и характеристики.
Базис S,K,I определяется при помощи константных функций, возвращающих комбинаторные термы в виде переменных с известными именами: i = Var "I"!, k = Var "K"!, s = Var "S"!.
Дополнительно, хотя это и не обязательно, можно реализовать
предикат, который проверяет, является ли заданная переменная
свободной в исследуемом комбинаторном терме. Этот предикат
определяется так:
free :: String -> Combinator -> Bool
free x (Var y) = x == y
free x (App e1 e2) = free x e1 || free x e2
free x (Lam y e) | x /= y = free x e
| x == y = False
Всё в полном соответствии с математическим определением.
Наконец, сама функция transform, которая осуществляет перевод комбинаторного терма в базис S,K,I. Её определение также выглядит в полном соответствии с перечисленными в предыдущем разделе правилами трансформации. Здесь можно видеть всю силу выразительности языка Haskell, которая позволяет записывать определения функций практически в математической нотации.
transform :: Combinator -> Combinator
transform (Var x) = Var x
transform (App x y) = App (transform x)
(transform y)
transform (Lam x (Var y))
| x == y = i
| otherwise = App k (Var y)
transform (Lam x (l@(Lam _ _))) = transform (Lam x (transform l))
transform (Lam x (App e1 e2)) = App (App s (transform (Lam x e1)))
(transform (Lam x e2))
Видно, что определение этой функции полностью совпадает с описанием правил трансформации комбинаторных термов. Однако данная функция не позволяет получить минимальное выражение комбинаторного терма в базисе S,K,I. Она возвращает один из возможных вариантов разложения терма. Например, комбинатор B, закодированный при помощи -нотации следующим образом:
b = Lam "x"
(Lam "y"
(Lam "z"
(App (Var "x")
(App (Var "y")
(Var "z")))))
Если передать это определение функции transform, то на выходе будет такая конструкция: S(S(KS)(S(KK)(S(KS)(S(KK)I))))(K(S(S(KS)(S(KK)I))(KI)))!
Представление данных и функций[править | править код]
Было бы странно, если бы комбинаторная логика не могла бы быть тем инструментом, при помощи которого можно было бы выражать различные объекты. Действительно, формализм комбинаторной логики, несмотря на весьма ограниченный алфавит, является вполне достаточным для выражения таких базовых понятий математики, как булевские значения истины, упорядоченные пары некоторых значений, натуральные числа, списки. Это, в свою очередь, позволяет практически полностью смоделировать теорию функционального программирования в рамках простой комбинаторной логики.
Сам по себе способ кодирования данных в рамках комбинаторной логики не является достаточно выразительным, более того, иной раз кажется, что такое кодирование вычурно и надумано. С точки зрения эффективности вычислений также имеются проблемы — оптимизация в прикладных трансляторах языков программирования позволяет кодировать и проводить вычисления над закодированными данными более эффективно. Однако этот способ кодирования данных является довольно интересным с точки зрения математики, т. к. позволяет понять, в том числе, и то, что данные могут нести внутри себя и способы их обработки.
Булевские значения[править | править код]
Для кодирования булевских величин необходимо иметь способ представления в комбинаторной логике значений true, false, а также служебную структуру if. Обычно для этих целей используются следующие правила кодирования:
- true K.
- false KI.
- if I.
Действительно, предложенный способ кодирования можно легко
проверить:
Как можно видеть, кодирование служебного слова if вообще не является необходимым — можно вполне обойтись и без него. Сами по себе значения истинности являются условными выражениями, т. к. возвращают первый или второй операнд в зависимости от своей природы. Поэтому комбинатор if является тождеством для трёх операндов, первый из которых должен быть значением истинности.
Вполне естественно, что над представленными значениями истинности должны иметься функции для выполнения базовых операций булевской логики. Такие базовые операции могут быть выражены через условные выражения. Способы кодирования трёх базисных булевских операций (отрицание, конъюнкция и дизъюнкция) выглядят следующим образом:
- not C(C if false) true.
- and B (CC false) if.
- or C if true.
Читателю предлагается самостоятельно проверить данные тождества на предмет их верности. Для этого необходимо рассмотреть таблицы истинности для перечисленных логических операций и сравнить их с традиционными таблицами истинности.
Нумералы Чёрча[править | править код]
Вполне понятно, что для кодирования чисел или подобных им объектов можно использовать любой способ выражения, главное, что потом на таком способе можно было бы построить приемлемые операции, тождественные тем, что определены для чисел. Поэтому, собственно, способов кодирования чисел существует множество. Но самым первым способом был тот, что предложен А. Чёрчем, и теперь носит наименование «нумералы Чёрча».
Нумералом Чёрча порядка называется такой объект ( — натуральное число из расширенного множества натуральных чисел ), который выражается через базовые комбинаторы следующим образом:
где под записью понимается -кратное приложение объекта к самому себе:
и т. д. Т. е. по индукции эти объекты можно определить как:
- .
- , .
По своей сути эти комбинаторы создают итеративное применение
заданной функции к некоторому аргументу, причём количество итераций
равно определяемому нумералом числу:
Для этих объектов довольно простым способом можно определить функции для сложения, умножения и возведения в степень. Это делается следующим образом:
- add CI(SB).
- mlt B.
- exp CI.
Доказательство данных тождеств легко проводится по индукции и предлагается для самостоятельной проработки.
Упорядоченные пары[править | править код]
Ещё один достаточно важный объект, имеющий большое практическое значение в функциональном программировании, является упорядоченная пара, состоящая из двух значений. Из пар создаются списки и списочные структуры, которые в свою очередь являются одним из основных объектов обработки в функциональных языках [3].
Для кодирования пары при помощи комбинаторных термов необходимо создать функцию, которая является конструктором такой пары. Это можно сделать следующим образом:
pair \(\equiv\) BC(CI)
Данный комбинатор составляет пару из двух заданных объектов любой природы. Для того, чтобы достать эти объекты из пары, необходимы т. н. «селекторы», т. е. функции для доступа к элементам пары. Эти селекторы можно определить так:
head \(\equiv\) CI true tail \(\equiv\) CI false
Эти комбинаторы «вынимают» первое или второе значение из переданной им на вход пары. Например, можно доказать, что выражение:
head (pair \(x\) \(y\)) = \(x\)
для любого выражения . Тоже самое можно сказать и о селекторе tail. Читателю опять же рекомендуется провести исследование этого выражения — это позволит закрепить изученный материал и более тонко понять смысл и назначение комбинаторной логики.
Общие замечания[править | править код]
Надо отметить, что предложенные способы кодирования данных и методов для их обработки при помощи инструментов комбинаторной логики является скорее не заданной догмой, но шаблонами, по которым можно производить вычисления над закодированными данными. Если рассмотреть такие способы кодирования более подробно, то видно, что и нумералы Чёрча, и упорядоченные пары могут принимать на вход не только сами значения для кодирования, но и функции для их обработки.
Так, определение пары является достаточно универсальным — оно не ограничивает понятие упорядоченной пары какими-то специальными рамками, а оставляет разработчику выбирать способ упаковки объектов в пару. Поэтому любая пара в качестве функции ожидает на вход некоторую функцию двух аргументов, которая после применения возвращает к изначальным объектам и определяет саму пару. Это значит, что и операции для распаковки пары (селекторы) должны быть различными в каждом конкретном случае. Приведённые выше определения являются шаблонами. Однако и эти шаблоны сами по себе также работают.
Все эти рассуждения касаются и остальных примеров. Это значит, что комбинаторная логика предоставляет учёным и разработчикам универсальный инструмент для абстрактного проектирования методов для решения широкого класса задач.
Заключение[править | править код]
Рассмотренное в этой статье введение в основы комбинаторной логики не претендует на целостность изложения, да и невозможно в малой научно-популярной статье изложить сложную науку о вычислениях, на которой основана реализация многих функциональных языков программирования. Поэтому всех заинтересовавшихся читателей можно отослать к изучению комбинаторной логики и -исчисления по учебникам, полноценно описывающим эти интереснейшие направления логики. В качестве направлений для дальнейшего изучения можно посоветовать рассмотреть следующие вопросы:
- Синтез нового объекта с заданными комбинаторными характеристиками.
- Использование редукции комбинаторов при помощи графов, что позволяет проводить ленивые вычисления, в том числе и потенциально бесконечных структур данных.
- Преобразование -местных операторных функций в каррированные,позволяющие производить частичные вычисления.
- Типизация комбинаторов, которая позволяет разбить всё множество комбинаторов на некие классы эквивалентности по их типам (сортам).
- Оболочка Каруби — специальная категория в рамках комбинаторной логики, при помощи которой кодируются все объекты операторных вычислений, включая их типы.
- Выражение при помощи комбинаторов различных систем программирования,в том числе выражение языков Lisp, Haskell и прочих.
- Изучение суперкомбинаторов — объектов для ленивого вычисления значений некоторых выражений.
- Оптимизация вычислений путём комбинирования параметров — шаг к построению систем суперкомпиляции.
- Техники проведения синтаксического анализа на функциональных языках программирования.
Автор оригинального текста статьи благодарит Антонюка Д. А., который помог написать функции на языке Haskell для трансформации комбинаторных термов в базис S,K,I
Примечания[править | править код]
- ↑ -исчисление—это наука о вычислениях, первоначально разработанная Алонзо Чёрчем для разрешения парадокса Б.Рассела о множестве всех множеств, не включающих самих себя в качестве подмножества. Рассмотрение этого направления логики выходит за рамки настоящей статьи.
- ↑ Кстати, первоначально Х. Карри ввёл в своей работе именно комбинаторы B и C. В дальнейшем первоначальный базис был упрощён.
- ↑ Например, первый функциональный язык LISP назван так из-за своего назначения — «LISt Processing» — «обработка списков».