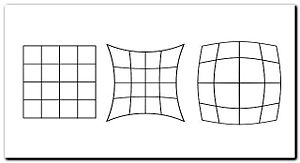
Дисторсия

Идеальное изображение, «подушка» и «бочка».

Дисто́рсия (от лат. distorsio, distortio — искривление) — аберрация оптических систем, при которой линейное увеличение изменяется по полю зрения. При этом нарушается линейное подобие между объектом и его оптическим изображением.

Исправляется подбором линз и других элементов оптической системы при её разработке. Если присутствует в цифровом изображении, может быть исправлена программно.

Дисторсия оптических систем с осевой симметрией

Это наиболее важный практический случай.

Прямые линии изображаются кривыми, кроме тех, которые лежат в одной плоскости с оптической осью. Например, изображение квадрата, центр которого пересекает оптическая ось, имеет вид подушки (подушкообразная дисторсия, подушка) при положительной дисторсии, и вид бочки (бочкообразная дисторсия, бочка) при отрицательной (см. рис.). В отдельных случаях искажения формы могут иметь и более сложный вид.

От диафрагмирования апертурной или виньетирующей диафрагмой дисторсия не зависит, поскольку таким способом невозможно изменить увеличение.

Количественно дисторсия может быть выражена через так называемую относительную дисторсию $\nu=\left[ (b-b_0)/b_0 \right] \cdot 100 \%$, где $b_0$ — линейное увеличение идеальной системы без дисторсии, $b$ — реальное увеличение. На оптической оси увеличение равно идеальному, отклонение от него обычно достигает максимума по краю поля зрения. Поэтому для характеристики дисторсии оптической системы обычно за $b$ берётся увеличение по краю.

Для одной и той же системы дисторсия зависит от расстояния до объекта, и, соответственно, от увеличения $b_0$. Как правило, если дисторсия мала или отсутствует при одном расстоянии, она будет мала и при другом.

Дисторсия зависит также и от длины волны, что даёт побочный эффект, сходный с хроматизмом увеличения, и может считаться хроматической аберрацией. Поэтому, строго говоря, дисторсия снижает разрешающую способность, хотя влияние этого обычно невелико.

В зрительных трубах и биноклях дисторсия может быть уничтожена практически полностью.

Дверные глазки, которые представляют собой широкоугольные зрительные трубы, намеренно изготавливаются с очень большой бочкообразной дисторсией, чтобы можно было, сохраняя широкий угол зрения, рассмотреть при большом увеличении лицо по центру.

Дисторсия фотообъективов

Дисторсия полностью отсутствует, если объектив симметричен, а линейное увеличение равно -1 — изображение перевёрнуто, его размер равен размеру предмета; такое увеличение соответствует возможной ситуации при макросъёмке. Под симметрией объектива здесь подразумевается зеркальная симметрия относительно плоскости, перпендикулярной оптической оси.

Для объективов, близких к симметричным, дисторсия обычно очень мала, даже если линейное увеличение не равно -1, что имеет место в подавляющем большинстве реальных случаев.

Исправление дисторсии в анастигматах без указанной симметрии также не представляет особой проблемы, в связи с тем, что паразитное отклонение лучей при дисторсии почти не ведёт к снижению разрешающей способности и намного менее заметно, чем сравнимое отклонение лучей при других аберрациях.

Характерная величина относительной дисторсии нормального объектива $\sim$ 0,5 % . В целом, у длиннофокусных объективов дисторсия меньше, чем у нормальных, у широкоугольных — больше.

Объективы с исправленной дисторсией называются ортоскопическим.

В некоторых случаях к исправлению дисторсии предъявляются повышенные требования. Так, в объективах для аэрофотосъемки относительная дисторсия составляет $\sim$ 0,01 %.

Иногда, напротив, величина дисторсии не важна. Объективы с неисправленной дисторсией называются дисторзирующими, они применяются, например, для метеорологических наблюдений.

В некоторые особо широкоугольные объективы дисторсия намеренно вводится для компенсации искажений перспективы и других недостатков (см. «рыбий глаз»).

От дисторсии следует отличать искажения перспективы, вызванные проектированием трёхмерного пространства на плоскость. При таких искажениях некоторые параллельные прямые линии на изображении выглядят не параллельными, некоторые вертикальные линии — наклонными, но к дисторсии это не относится (См. Коррекция перспективы).

Теория

Из всех геометрических аберраций дисторсия описывается наиболее просто. Пусть $\vec r=(y,z)$ — вектор, задающий две координаты в плоскости, расположенной перпендикулярно оптической оси (координата $x$ вдоль оси сюда не входит). Для идеального изображения все лучи, вышедшие из точки с координатами $\vec r$ и прошедшие через оптическую систему, попадут в точку изображения с координатами $\vec R$, которые определяются по формуле:

$\vec R=b_0 \, \vec r$ ,

где $b_0$ — коэффициент линейного увеличения. Если присутствует дисторсия третьего порядка (бывает только нечётных порядков: третьего, пятого, седьмого и т. д.), тогда лучи из $\vec r$ попадут в

$\vec R=b_0 \, \vec r + F_3 \, r^2 \cdot \vec r$,

где $r$ — длина $\vec r$, $F_3$ — дисторсия третьего порядка, которая обычно вносит наибольший вклад в искажение формы. Если $F_3$ имеет тот же знак, что и $b_0$, возникнет «подушка», в противном случае — «бочка».

Если есть дисторсия высших порядков $F_{n>3}$, тогда лучи из $\vec r$ попадают в

$\vec R=b_0 \, \vec r + F_3 \, r^2 \cdot \vec r + F_5 \, r^4 \cdot \vec r + F_7 \, r^6 \cdot \vec r +...$

В этом случае искажения формы могут иметь более сложный вид, хотя на практике (например, в фотографии) это можно увидеть очень редко. $F_n$ зависят от расстояния до изображаемого предмета и от длины волны.

Если нужно учитывать другие аберрации, то в выражение для $\vec R$ добавляются другие слагаемые, зависящие не только от $\vec r$, но и от координат луча во входном зрачке.

Литература

• Волосов Д.С. Фотографическая оптика. М., «Искусство», 1971.
• Русинов М.М. Композиция оптических систем. Л., «Машиностроение», 1989.
• Сивухин Д.В. Общий курс физики. Оптика. М., «Наука», 1985.