Дифракция
Дифра́кция во́лн (лат. diffractus — буквально разломанный, переломанный) — прежде всего явления,наблюдаемые при прохождении волн мимо края препятствия, связанные с отклонением волн от прямолинейного распространения при взаимодействии с препятствием, также это явление можно рассматривать как отклонение от законов геометрической оптики при распространении волн.
Первоначально понятие дифракции относилось только к огибанию волнами препятствий, но в современном, более широком толковании, с дифракцией связывают весьма широкий круг явлений, возникающих при распространении волн в неоднородных средах, а также при распространении ограниченных в пространстве волн. Дифракция тесно связана с явлением интерференции. Более того, само явление дифракции зачастую трактуют как частный случай интерференции (интерференция вторичных волн).[1]
Дифракция волн наблюдается независимо от их природы и может проявляться:
- в преобразовании пространственной структуры волн. В одних случаях такое преобразование можно рассматривать как «огибание» волнами препятствий, в других случаях — как расширение угла распространения волновых пучков или их отклонение в определенном направлении;
- в разложении волн по их частотному спектру;
- в преобразовании поляризации волн;
- в изменении фазовой структуры волн.
Дифракционные эффекты зависят от соотношения между длиной волны и характерным размером неоднородностей среды либо неоднородностей структуры самой волны. Наиболее сильно они проявляются при размерах неоднородностей сравнимых с длиной волны. При размерах неоднородностей существенно превышающих длину волны (на 3-4 порядка и более), явлением дифракции, как правило, можно пренебречь. В последнем случае распространение волн с высокой степенью точности описывается законами геометрической оптики. С другой стороны, если размер неоднородностей среды много меньше длины волны, то в таком случае вместо дифракции часто говорят о явлении рассеяния волн.
Наиболее хорошо изучена дифракция электромагнитных (в частности, оптических) и акустических волн, а также гравитационно-капиллярных волн (волны на поверхности жидкости).[2]
Тонкости в толковании термина «дифракция»[править | править код]
В явлении дифракции важную роль играют исходные размеры области волнового поля и исходная структура волнового поля, которая подвержена существенной трансформации в случае, если элементы структуры волнового поля сравнимы с длиной волны или меньше её. Например, ограниченный в пространстве волновой пучок имеет свойство «расходиться» («расплываться») в пространстве по мере распространения даже в однородной среде. Данное явление, не описывается законами геометрической оптики и относится к дифракционным явлениям (дифракционная расходимость, дифракционное расплывание волнового пучка). Исходное ограничение волнового поля в пространстве и его определенная структура могут возникнуть не только за счет присутствия поглощающих или отражающих элементов, но и, например, при порождении (генерации, излучении) данного волнового поля.
Изначально явление дифракции трактовалось как огибание волной препятствия, то есть проникновение волны в область геометрической тени. Следует заметить, что в средах, в которых скорость волны плавно (по сравнению с длиной волны) меняется от точки к точке, распространение волнового пучка является криволинейным (см. градиентная оптика, градиентные волноводы, мираж). При этом волна также может огибать препятствие. Однако такое криволинейное распространение волны может быть описано с помощью уравнений геометрической оптики, и это явление не относится к дифракции. Отступление от прямолинейности распространения света наблюдается также в сильных полях тяготения. Экспериментально подтверждено, что свет, проходящий вблизи массивного объекта, например, вблизи звезды, отклоняется в ее поле тяготения в сторону звезды. Таким образом, и в данном случае можно говорить об «огибании» световой волной препятствия. Однако, это явление также не относится к дифракции. Вместе с тем, во многих случаях дифракция может быть и не связана с огибанием препятствия. Такова, например, дифракция на непоглощающих (прозрачных) так называемых фазовых структурах.
С точки зрения современной науки определение дифракции как огибания светом препятствия признается недостаточным (слишком узким) и не вполне адекватным.
Поскольку, с одной стороны, явление дифракции света оказалось невозможным объяснить с точки зрения лучевой модели, то есть с точки зрения геометрической оптики, а с другой стороны, дифракция получила исчерпывающее объяснение в рамках волновой теории, то часто под дифракцией понимают проявление любого отступления от законов геометрической оптики. При этом следует заметить, что некоторые волновые явления не описываются законами геометрической оптики и, в то же время, не относятся к дифракции. К таким типично волновым явлениям относится, например, вращение плоскости поляризации световой волны в оптически активной среде, которое дифракцией не является. Вместе с тем, единственным результатом так называемой коллинеарной дифракции с преобразованием оптических мод может быть именно поворот плоскости поляризации, в то время как дифрагированный волновой пучок сохраняет исходное направление распространения. Такой тип дифракции может быть реализован, например, как дифракция света на ультразвуке в двулучепреломляющих кристаллах, при которой волновые векторы оптической и акустической волн параллельны друг другу. Еще один пример: с точки зрения геометрической оптики невозможно объяснить явления, имеющие место в так называемых связанных волноводах, хотя эти явления также не относят к дифракции (волновые явления, связанные с «вытекающими» полями).
Общим свойством всех эффектов дифракции является именно определенная зависимость данного явления от соотношения между длиной волны и размером неоднородностей среды. Поэтому дифракция представляет собой универсальное волновое явление и характеризуется одними и теми же законами в случае волн разной природы.
Амплитудные и фазовые неоднородности[править | править код]
Частные случаи дифракции[править | править код]
Огибание препятствия волнами на поверхности жидкости[править | править код]
Дифракция света на краю экрана. Граница тени[править | править код]
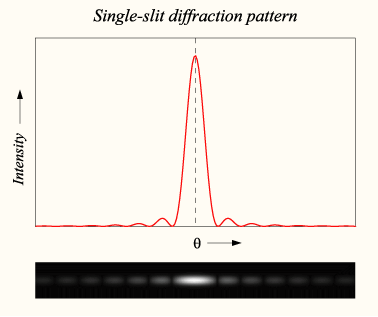
Дифракция на щели[править | править код]
В качестве примера рассмотрим дифракционную картину возникающую при прохождении света через щель в непрозрачном экране. Мы найдём интенсивность света в зависимости от угла в этом случае.
Математическое представление принципа Гюйгенса используется для написания исходного уравнения.
Рассмотрим монохроматическую плоскую волну с амплитудой с длиной волны λ падающую на экран с щелью, ширина которой a.
Если разрез находится в плоскости x′-y′, с центром в начале координат, тогда может предполагаться, что дифракция производит волну ψ на расстоянии r, которая расходится радиально и вдалеке от разреза можно записать:
пусть (x′,y′,0) — точка внутри разреза, по которому мы интегрируем. Мы хотим узнать интенсивность в точке (x,0,z). Щель имеет конечный размер в x направлении (от до ), и бесконечна в y направлении ([, ]).
Расстояние r от щели определяется как:
Предполагая случай дифракции Фраунгофера, получим условие . Другими словами, расстояние до точки наблюдения много больше характерного размера щели (ширины). Используя биноминальное разложение и пренебрегая слагаемыми второго и выше порядков малости, можно записать расстояние в виде:
Видно, что 1/r перед уравнением не осциллирует, то есть даёт малый вклад в интенсивность по сравнению с экспоненциальным множителем. И тогда его можно записать приближённо как z.
Здесь мы введём некую константу 'C', которой обозначим все постоянные множители в предыдущем уравнении. Она, в общем случае может быть комплексной, но это не важно, так как в конце нас будет интересовать только интенсивность, и нам будет интересен только квадрат модуля.
В случае диффракции фраунгофера мало, поэтому . такое же приближение верно и для . Таким образом, считая , приводит к выражению:
Используя формулу Эйлера и её производную: и .
где ненормированная синкус функция определена как .
Подставляя в последнее выражение для амплитуды, можно получить ответ для интенсивности в виде волны в зависимости от угла θ:
См. также Дифракция на N-щелях
Дифракция на отверстии[править | править код]

Фокусировка света[править | править код]
Дифракция звука и ультразвуковая локация[править | править код]
Дифракция радиоволн и радиолокация[править | править код]
Дифракционная решётка[править | править код]
Подробно на страничке: http://www.college.ru/WaveOptics/content/chapter1/section3/paragraph1/theory.html
Дифракция рентгеновских лучей в кристаллах и рентгеноструктурный анализ[править | править код]
Дифракция света на ультразвуке[править | править код]
Дифракция электронов[править | править код]
Дифракция других частиц (нейтронов, атомов, молекул)[править | править код]
История исследований[править | править код]
Основы теории дифракции были заложены при изучении дифракции света в первой половине XIX века в трудах Юнга и Френеля. Среди других ученых, которые внесли значительный вклад в изучение дифракции: Гримальди, Гюйгенс, Араго, Пуассон, Гаусс, Фраунгофер, Бабине, Кирхгоф, Аббе, У. Г. Брэгг и У. Л. Брэгг, фон Лауэ, Роуланд, Зоммерфельд, Леонтович, Фок, Ван-Циттерт, Цернике (см. История оптики, дифракция света)).
Обнаружение дифракции частиц (электронов) в 1927 году (опыт Дэвиссона и Джермена) сыграло большую роль в подтверждении существования волн де Бройля и в подтверждении концепции корпускулярно-волнового дуализма (идеи двойственной природы волн и частиц). В XX и XXI веках продолжились исследования дифракции волн на сложных структурах.[3]
См. также[править | править код]
Общие трактовки и теории дифракции, важнейшие утверждения[править | править код]
Трактовка явления дифракции Юнга
Принцип Гюйгенса-Френеля. Дифракция как интерференция вторичных волн
Трактовка дифракции Френеля
Теория дифракции Кирхгофа. Интеграл Кирхгофа
Модель поперечной диффузии амплитуды (в теории дифракции). Уравнение Леонтовича
Дифракция на инверсных структурах (дифракция на дополнительных экранах).
- Принцип Бабине (теорема Бабине)
Дифракция с точки зрения квантовой теории
- Корпускулярно-волновой дуализм частиц и волн
- Волны де Бройля. Частицы как волновые пакеты
- Волны как частицы. Фотон, фонон, магнон и другие квазичастицы
- Дифракция как следствие соотношения неопределенности Гейзенберга
Дифракция объектов разной природы (волн и частиц)[править | править код]
Дифракция света, дифракция оптических волн
- История изучения дифракции (света)
- Дифракция света на спиновых волнах
- Дифракция света на фоторефрактивных решётках
- Оптическая голография
- Оптическая томография
Дифракция радиоволн
Дифракция рентгеновских лучей
- Рентгеновская (радиационная) томография
Дифракция звука, дифракция акустических волн
- Акустическая (ультразвуковая) томография
Дифракция гравитационно-капиллярных волн (волн на поверхности жидкости)
Дифракция частиц
Дифракция неклассических волновых полей (дифракционная эволюция сжатых состояний света и т. п.)
Дифракция на различных типах структур среды[править | править код]
Дифракция заданного волнового поля в однородной среде
- Дифракционная расходимость волновых пучков
- Дифракция свободного гауссова пучка
- Дифракционный предел оптических приборов
- Дифракционный предел электронного микроскопа
Дифракция на амплитудных, фазовых и амплитудно-фазовых неоднородностях;
- Дифракционная (фазовая) линза (Френеля)
- Дифракция и рефракция света на фазовых структурах
Дифракция на пропускающих и отражающих структурах
Дифракция на структурах с резкими границами
- Дифракция на крае экрана. «Оптический нож»
- Дифракция на щели, отверстии, на компактном препятствии
- Зоны Френеля. Основные приближения и зоны дифракции
- Прожекторная зона
- Приближение ближней зоны дифракции (дифракция Френеля)
- Приближение дальней зоны дифракции (дифракция Фраунгофера)
- Промежуточная зона дифракции (промежуточная область между дифракцией Френеля и Фраунгофера)
- Пятно Пуассона (пятно Араго-Пуассона)
- Дифракция на круглом, квадратном, прямоугольном, треугольном, шестиугольном отверстиях и отверстии произвольной формы
- Дифракция на двух щелях, отверстиях, препятствиях
- Дифракция на N щелях
- Дифракция скользящих волн. Граница раздела среды с разными свойствами перпендикулярна волновому фронту волны хотя бы в одной точке. При этом волна распространятеся («скользит») вдоль поверхности.
- Дифракция скользящей волны над плоской поглощающей поверхностью.
- Дифракция скользящей волны над поглощающей цилиндрической поверхностью.
- Дифракция скользящей волны на заднем закруглении.
- Дифракция скользящей волны на переднем закруглении
Дифракция на градиентных структурах (структурах с плавным изменением параметров среды в пространстве)
Дифракция на неупорядоченных структурах и рассеяние света
Дифракция на упорядоченных структурах
- Дифракционные решётки (дифракция на периодических структурах)
- Дифракционные решётки с определенным профилем
- Дифракционные решётки с прямоугольным профилем
- Бигармонические дифракционные решётки
- Дифракционные решётки с треугольным пофилем
- Дифракционные решётки со сложным профилем
- Ограниченные дифракционные решётки, дифракция ограниченных пучков на периодических структурах
- Дифракционные решётки различной размерности
- Дифракция на одномерных и двумерных периодических структурах
- Плоские дифракционные структуры с одномерной и двумерной периодичностью
- Неплоские дифракционные структуры. Фокусирующие (вогнутые) дифракционные решетки. Круг Роуланда.
- Дифракция на объемных периодических структурах
- Дифракция на объемных структурах с двумерной и трехмерной периодичностью
- Дифракция света в фотонных кристаллах
- Методы создания дифракционных решёток
- Нарезные дифракционные решётки
- Реплики
- Дифракционные решётки на основе жидкокристаллических транспарантов
- Акустические (ультразвуковые) дифракционные решётки
- Дифракционные решётки, индуцированные спиновыми волнами
- Фоторефрактивные дифракционные решётки
- Дифракционные решётки, наведенные в нелинейной среде с помощью интерференции волн
- Дифракция на фазовой решётке в анизотропной среде.
- Акустооптическая дифракция в двулучепреломляющих средах
- Коллинеарная и квазиколлинеарная дифракция
- Коллинеарная дифракция и многослойные интерференционные структуры
- Дифракция на непериодических упорядоченных структурах
- Дифракционные решётки с переменной амплитудой профиля
- Дифракция света на затухающей акустической волне
- Дифракционные решётки с переменным шагом
- Дифракционные оптические элементы
- Дифракция на квазикристаллических структурах
Дифракция волн с различными характеристиками[править | править код]
- Дифракция монохроматических и немонохроматических волн
- Дифракционные решетки как спектральные фильтры.
- Дифракция плоских, сферических и других неплоских волн
- Дифракция однородных и неоднородных волн (заданное распределение амплитуды вдоль волнового фронта равномерное или нет)
- Дифракция когерентных, некогерентных и частично когерентных волн. Трансформация параметров когерентности волны (радиуса когерентности и др.) при дифракции
Дифракционные приборы, дифракционные элементы, преобразующие волновые поля заданным образом[править | править код]
- Дифракционная теория изображений, теория Аббе
- Пространственная фильтрация волновых полей
- Оконтуривание (пространственное дифференцирование) изображений
- Сложные дифракционные преобразователи волновых полей (дифракционные элементы). См. [Методы компьютерной оптики. Под ред. В. А. Сойфера — М.: ФИЗМАТЛИТ, 2003]
Дифракция на динамических структурах[править | править код]
Аналогии между дифракцией и другими волновыми явлениями[править | править код]
- Теория связанных мод для дифракции и нелинейно-оптических явлений (аналогия между коллинеарной АО дифракцией и генерацией второй гармоники. Теория связанных мод практически одна и та же)
- Дифракция и связанные волноводы
Литература[править | править код]
- Ландау Л.Д., Лифшиц Е.М.: Теория поля|1988
- Сивухин Д.В.:Оптика:2002
Ссылки[править | править код]
- ↑ http://www.oval.ru/enc/23938.html
- ↑ Книга:Ландау Л.Д., Лифшиц Е.М.: Теория поля|1988
- ↑ Книга:Сивухин Д.В.:Оптика:2002
- Демонстрации по оптике (Java-аплеты): дифракция Френеля на круглом отверстии и на полуплоскости, дифракция Фраунгофера на щели