Пропорция (математика)

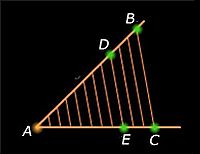
Рис.1, Пропорция отрезков, например,AB:АС = AG:AE

‎Пропо́рция (математика) (лат. proportio — соразмерность, выровненность частей), равенство отношений числовых величин, т. е. равенство вида a : b = c : d (AB:AC=AD:AE) или, в других обозначениях, равенство $\ \frac ab=\frac cd$ (часто читается как: «a относится к b так же, как c относится к d»). Если a : b = c : d, то a и d называют крайними, а b и c — средними членами пропорции. ^[1]

Где:

AB = a — отрезок (крайний)
AC = b — (средний)
AD = c — (средний)
AE = d — (крайний)

Пропорция (математика) в отличие от золотого сечения содержит разные значения средних членов (вместо b·b имеем b·c или b·c = a·d).

Основные свойства пропорций[править | править код]

Обращение пропорции. Если возьмём соотношения в виде: a : b = c : d, то b : a = d : c
Перемножение членов пропорции крест-накрест. Если a : b = c : d, то ad = bc.
Перестановка средних и крайних членов. Если a : b = c : d, то

a : c = b : d (перестановка средних членов пропорции),

d : b = c : a (перестановка крайних членов пропорции).

Увеличение и уменьшение пропорции. Если a : b = c : d, то

(a + b) : b = (c + d) : d (увеличение пропорции),

(a – b) : b = (c – d) : d (уменьшение пропорции).

Составление пропорции сложением и вычитанием. Если a : b = c : d, то

(a + с) : (b + d) = a : b = c : d (составление пропорции сложением),

(a – с) : (b – d) = a : b = c : d (составление пропорции вычитанием).

Золотое сечение[править | править код]

Основная статья: Золотое сечение

Файл:Zolotoe setshenie.jpg

(Рис.2) Cхема пропорциональных отрезков золотого сечения

‎Золотое сечение (золотая пропорция, гармоническое деление, деление в крайнем и среднем отношении) — соотношение числовых величин в математике и искусстве: отношение суммы двух величин к большей из них равно отношению большей величины к меньшей

Отношение частей в этой пропорции выражается квадратичной иррациональностью $\varphi = \frac{ \sqrt{5}+1}{2} \approx 1{,}6180339887\dots$

Т. е. (см.Рис.2) равенство вида (a + b):a = a : b, или, в других обозначениях, равенство $\! \frac {a + b}{a}=\frac {a}{b}=\phi$ (часто читается как: «(a + b) относится к a так же, как a относится к b»). Если (a + b):a = a : b, то (a + b) и b называют крайними, а a — средними членами пропорции.^[2]

Золотое сечение в отличие от пропорции содержит произведение определённых значений средних членов (вместо c·d имеем a·a или a·c = a·a). Не любое деление отрезка даёт среднее сечение. Например, деление отрезка на части, выраженных рациональными числами или на равные части, не даёт золотого сечения.

В дошедшей до нас античной литературе деление отрезка в крайнем и среднем отношении (ἄκρος καὶ μέσος λόγος) впервые встречается в «Началах» Евклида (ок. 300 до н. э.), где оно применяется для построения правильного пятиугольника.

Лука Пачоли, современник и друг Леонардо да Винчи, называл это отношение «божественной пропорцией». Термин «золотое сечение» (goldener Schnitt) был введён в обиход Мартином Омом в 1835 году.

Золотое сечение и иррациональность[править | править код]

Золотое сечение в пятиконечной звезде

$\varphi$ — иррациональное алгебраическое число, положительное решение квадратного уравнения

$\varphi^2 = \varphi + 1.$

$\varphi$ представляется в виде бесконечной цепочки квадратных корней:

$\varphi = \sqrt{1 + \sqrt{1 + \sqrt{1 + \sqrt{1 + ...}}}}.$

$\varphi\;$ представляется в виде бесконечной цепной дроби

$\varphi = 1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1+\,\cdots}}},$

подходящими дробями которой служат отношения последовательных чисел Фибоначчи

\frac{F_{n+1}}{F_n}

. Таким образом,

\varphi = \lim_{n\to\infty} \frac{F_{n+1}}{F_n}

.

Построение золотого сечения

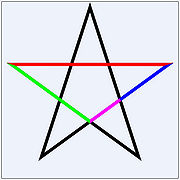
В правильной пятиконечной звезде каждый отрезок делится пересекающим его отрезком в золотом сечении (на приведённом рисунке отношение красного отрезка к зелёному, так же как зелёного к синему, так же как синего к фиолетовому, равны $\varphi$ ).

Геометрическое построение. Золотое сечение отрезка $AB$ можно построить следующим образом: в точке $B$ восстанавливают перпендикуляр к $AB$ , откладывают на нём отрезок $BC$ , равный половине $AB$ , на отрезке $AC$ откладывают отрезок $AD$ , равный $AC-CB$ , и наконец, на отрезке $AB$ откладывают отрезок $AE$ , равный $AD$ . Тогда

$\varphi=\frac{|AB|}{|AE|}=\frac{|AE|}{|EB|}.$

Золотое сечение — пропорция и гармония в искусстве[править | править код]

Длительное время существовало общепринятое суждение, что объекты, содержащие в себе «золотое сечение», воспринимаются людьми как наиболее гармоничные. Например, пропорции золотого сечения находят в пирамиде Хеопса, в соотношении размеров некоторых храмов, барельефов; предметов быта и украшений из гробницы Тутанхамона. По мнению первых исследователей, это свидетельствует, что египетские мастера пользовались соотношениями золотого сечения при их создании.

Согласно Ле Корбюзье, в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют золотому сечению. Древнеегипетский зодчий Хесира, вырезанный на деревянной доске, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого сечения. В фасаде древнегреческого храма Парфенона также присутствуют золотые пропорции. В циркуле из древнеримского города Помпеи (музей в Неаполе) также заложены пропорции золотого деления, и т. д. и т. п.

К тем же выводам пришёл Розенов в статье «Закон золотого сечения в поэзии и музыке» (1925) на примере произведений Баха, Моцарта, Бетховена.

Критика[править | править код]

Ко подобным утверждениям следует относиться с должной критичностью, поскольку во многих случаях это может оказаться результатом подгонки или совпадения (эффект «числовой мистики»). Есть обоснованные данные, что значимость золотого сечения в искусстве, архитектуре и в природе преувеличена, и основывается на ошибочных расчётах. ^[3]

При обсуждении оптимальных соотношений сторон прямоугольников (размеры листов бумаги A0 и кратные, размеры фотопластинок (6:9, 9:12) или кадров фотоплёнки (часто 2 : 3), размеры кино- и телевизионных экранов — например, 3:4 или 9:16) были испытаны самые разные варианты. Оказалось, что большинство людей не воспринимает золотое сечение как оптимальное и считает его пропорции «слишком вытянутыми».

Литература[править | править код]

ван дер Варден, Б. Л. Пробуждающаяся наука. Математика Древнего Египта, Вавилона и Греции. — пер. с голл. И. Н. Веселовского — М.: ГИФМЛ, 1959

См. также[править | править код]

Ссылки[править | править код]

Это незавершённая статья по математике.
Вы можете помочь «Традиции», исправив и дополнив эту статью.

[1] ttp://bse.sci-lib.com/article093423.html

[2] ttp://bse.sci-lib.com/article093423.html

[3] Радзюкевич А. В. Красивая сказка о «золотом сечении»

[1]

[2]

[3]