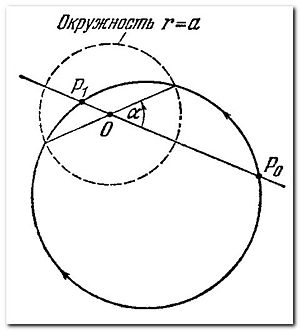
«Рыбий глаз» Максвелла
«Рыбий глаз» Максвелла (1854) — абсолютная оптическая система, представляющая неоднородную сферически-симметричную среду, характеризующуюся показателем преломления
,
где — расстояние до центра системы , и — параметры.
Каждый луч представляет собой окружность, не проходящую через , или прямую, проходящую через . Изображение точки, создаваемое системой, удобно строить по прямому лучу: все лучи из произвольной точки собираются в точке , лежащей на прямой, которая соединяет с ; и расположены по разные стороны от , и произведение
.
Следовательно, «рыбий глаз» Максвелла является абсолютной оптической системой, в которой отображение осуществляется преобразованием инверсии. Плоскость, не проходящая через , изображается сферой.
В этой системе отсутствуют все аберрации, кроме дисторсии и кривизны поля изображения.