Диафрагма (оптика)
Диафрагма (от греч. διάφραγμα — перегородка) — оптическое устройство, компонент оптической системы (а также анатомическое образование, элемент глаза позвоночных) - непрозрачная преграда, ограничивающая поперечное сечение световых пучков в оптических устройствах (микроскоп, зрачок, фотоаппарат, телескоп, дальномер и др.).
Виды диафрагм[править | править код]
Названия видов диафрагм определяются тем, в какой части оптической системы они используются и какую часть пучка света ограничивают. Если вид диафрагмы не уточняется, как правило, имеется в виду:
- Общая или полевая диафрагма;
- Апертурная диафрагма.
Общая или полевая диафрагма[править | править код]
Полевая диафрагма, диафрагма поля зрения — непрозрачная преграда, ограничивающая линейное поле оптической системы в пространстве предметов или в пространстве изображений.
Располагается в непосредственной близости от одного из фокусов оптической системы (в системах с оборачивающими элементами может располагаться в одном из промежуточных фокусов). Может иметь форму круга (в микроскопах, телескопах). В спектральных приборах имеет форму щели.
Она определяет, какая часть пространства может быть изображена оптической системой.
Из центра входного зрачка диафрагма поля зрения видна под наименьшим углом.
Согласно теории Эбби образование оптического изображения, развитой в 1873 году, следует, что способность получения оптического изображения в конечном счете ограничена прхождением лучей света, исходящих из источника света или отражённых лучей из каждой точки изображения из-за явления дифракции. Если апертура (отверстие) оптического компонента не достаточно большая (полностью открытая диафрагма, например, объектива), которая не позволяет собрать весь дифрагированный свет, то более прекрасные виды оптического изображения не будут соответствовать точно объекту (изображению).
Расчёт полевой диафрагмы[править | править код]
Минимальный размер отверстия при диафрагмировании (d) для оптического компонента, ограниченного его размером апертуры, выражено в соответствии с критерием Рэлея:
- λ0 — длина волны в вакууме;
- NA - числовая апертура en:Numerical_aperture для показателя преломления (обычно 1.3–1.4 для современных целей (например, для обычной микроскопии)).
И соответственно предел максисального отверстия (минимального диафрагмирования) — обычно находится в пределах λ0/2 (т.е. полуволны).[2]
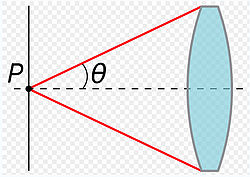
В большинстве областей оптики, и особенно в микроскопии, числовая апертура оптической системы, типа линзы объектива определена
- n - показатель преломления среды, в которой линза работает (1.0 для воздуха, 1.33 для чистой воды, и до 1.56 для нефти),
- θ — полуугол максимального конуса света, который может войти или выйти из линзы. Вообще, это - угол реального крайнего луча в системе. Угловая апертура линзы - приблизительно эта двойная ценность (в пределах параксиального приближения).
- NA — числовая апертура вообще измеряется относительно специфического объекта, или даёт оптическое изображение и указывает его изменение, поскольку просматриваемый пункт перемещен.
Применение[править | править код]
В микроскопии, NA важен, потому что это указывает власть решения линзы. Размер самых прекрасных деталей, которые могут быть решены, пропорционален λ/NA, где λ — длина волны света. Линза с большей числовой апертурой будет в состоянии визуализировать более прекрасные детали чем линза с меньшей числовой апертурой. Линзы с большими числовыми апертурами также собирают больше света и будут вообще обеспечивать более яркое изображение.
Числовая апертура используется, чтобы определить размер ямы в оптических форматах диска.[3]
Апертурная диафрагма[править | править код]
Апертурная диафрагма, действующая диафрагма — располагается вблизи центра формирующей оптическое изображение оптической системы. Её изображение, сформированное предшествующей (по ходу лучей) частью оптической системы, определяет входной зрачок системы. Сформированное последующей частью — выходной зрачок.
Входной зрачок ограничивает угол раскрытия пучков лучей, идущих от точек объекта; выходной зрачок играет ту же роль для лучей, идущих от оптического изображения объекта.
С увеличением диаметра входного зрачка (действующего отверстия оптической системы) растёт освещённость изображения.
Уменьшение до известного предела действующего отверстия оптической системы (диафрагмирование) улучшает качество изображения, так как при этом из пучка лучей устраняются краевые лучи, на ходе которых в наибольшей степени сказываются аберрации.
Диафрагмирование увеличивает также глубину резкости (глубину резко изображаемого пространства). В то же время, уменьшение действующего отверстия снижает, из-за дифракции света на краях диафрагмы, разрешающую способность оптической системы. В связи с этим апертура оптической системы должна иметь оптимальное значение.
Расчёт диафрагмы[править | править код]
Числовая апертура не используется в фотографии. Вместо этого используется угловая апертура линзы (или зеркало отображения), выраженое f — числом
- таким образом
(Принимается нормальное использование диафрагмы в воздухе (n = 1)).
Принимается, когда числовая апертура является маленькой, и это почти точно также и в больших числовых апертурах для хорошо отъюстированных объективов камеры. Для числовых апертур меньше чем приблизительно 0.5 (f-числа, больше чем приблизительно 1) расхождение между приближением и полным выражением - меньше чем 10 %. Вне этого нарушается допуск точности. Поскольку Радолф Кингслэйк объясняет, Это - общая ошибка предположить, что отношение [D / 2f] фактически равно
Применения[править | править код]
- Кадровая рамка в фото- и киноаппаратах, фотоувеличителях также является полевой диафрагмой.
- Кадрирующая рамка и рамки-виньетки, используемые при печати фотоснимков, также являются разновидностью полевой диафрагмы.
- При макросъёмке иногда применяется полевая диафрагма в виде рамки, окружающей объект и служащей своеобразным «видоискателем».
- Примером изменяемой полевой диафрагмы в съёмочной аппаратуре являются дополнительные шторки, ограничивающие кадровое окно по вертикали в плёночном фотоаппарате Pentax Z1P для получения снимка с панорамным соотношением сторон кадра.
- Изменение с помощью кадрового окна размеров кадра в процессе съёмки или монтажа фильма позволяет создавать вариоскопическое кино (наиболее известны фильмы «Нетерпимость» 1916 года, «Дверь в стене» 1956 года).
Бленды[править | править код]
Другие диафрагмы, имеющиеся в оптической системе, главным образом препятствуют прохождению через систему лучей, расположенных в стороне от главной оси оптической системы. Аналог внешней диафрагмы, находящийся перед оптической системой кино- и фотоаппаратов, называют светозащитной блендой или просто блендой.
Точную границу между блендой и полевой диафрагмой провести невозможно, однако часто считается, что если изображение границ перегородки, сформированное оптической системой, является или может быть получено резким (в процессе фокусировки), эта перегородка является полевой диафрагмой. В противном случае речь идёт о бленде.
Устройство и некоторые применения диафрагм[править | править код]
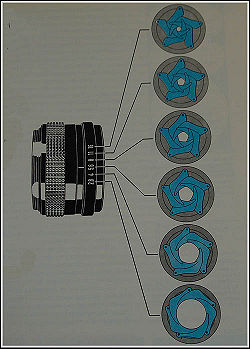
Роль диафрагмы часто играют зачернённые элементы оправы линз, призм, зеркал и др. оптических деталей, зрачок глаза, границы освещённого предмета, в спектроскопе — щелевая диафрагма, в фотоаппаратах — ирисовая или ступенчатая диафрагма.
Размер и положение диафрагмы определяют поле зрения, освещённость и качество изображения, глубину резкости и разрешающую способность оптической системы.
Управляемые диафрагмы[править | править код]
В фото-киносъёмочной оптике[править | править код]
В системах растрирования[править | править код]
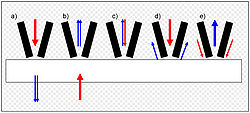
В полиграфии, в системах электронного растрирования полутоновых изображений, применялась электрически управляемая диафрагма (электромагнитная или электрическая), являющаяся разновидностью полевой диафрагмы и формирующая размер и форму светового пятна в элементе растра в зависимости от подаваемого сигнала.
Развитие цифровых методов печати привело к вытеснению такого оборудования из-за ограниченности быстродействия механической части устройства.
См. также[править | править код]
Примечания[править | править код]
- ↑ G. Kaupp (2006). Atomic Force Microscopy, Scanning Nearfield Optical Microscopy and Nanoscratching: Application to Rough and Natural Surfaces. Heidelberg: Springer. ISBN 3540284052.
- ↑ E. Hecht (2002). Optics. San Francisco: Addison Wesley. ISBN 0195108183.
- ↑ "High-def Disc Update: Where things stand with HD DVD and Blu-ray" by Steve Kindig, Crutchfield Advisor. Accessed 2008-01-18.
- ↑ Greivenkamp, John E. (2004). Field Guide to Geometrical Optics. SPIE Field Guides vol. FG01. SPIE. ISBN 0-8194-5294-7. http://books.google.com/books?id=1YfZNWZAwCAC&pg=PA29&dq=inauthor:greivenkamp+numerical-aperture&lr=&as_brr=0&as_pt=ALLTYPES&ei=CgxxSf2gGojClQTSs4SODg. p. 29.
- ↑ Rudolf Kingslake (1951). : The Practical Guide to Optics for Photographers. Case-Hoyt Corp. for Garden City Books. pp. 97–98. http://books.google.com/books?id=9u2WGQAACAAJ&dq=intitle:photography+inauthor:kingslake&lr=&as_brr=0&as_pt=ALLTYPES&ei=HQtxSd_-B5LYlQSfkImeDg.
Литература[править | править код]
- Ландсберг Г. С. Оптика, 4 изд., 1957
- Слюсарев Г. Г. Геометрическая оптика, — Л., 1946;
- Тудоровский А. И. Теория оптических приборов, 2 изд., т. 1-2, — Л., 1948-1952.
- Гл.ред. Е. А. Иофис Фотокинотехника.
- Энциклопедия.: «Советская Энциклопедия», 1981. Статьи «Апертурная диафрагма», «Полевая диафрагма». Статья «Вариоскопическое кино». Автор М. З. Высоцкий.