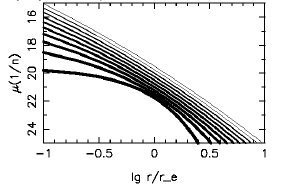
Закон Серсика
Введение[править | править код]
| Текущая версия статьи по астрономии. Помогите Традиции, исправьте и дополните её. |
Закон Серсика — эмпирический закон распределения поверхностной яркости галактики, является обобщением закона Вокулера.
Формулу Серсика, которая является обобщением закона Вокулера, часто записывают в следующем виде:
\(I(r) = I_0 e^{-\nu_n \alpha^{1/n}}\),
где I0 - центральная поверхностная яркость, α = r / re, n - положительное действительное число и νn - константа, выбираемая так, чтобы в пределах re излучалась половина полной светимости. В более похожем на закон Вокулера виде (формула
\(\frac{I(r)}{I_e} = exp\left [- \nu_n (\left [\frac{r}{r_e}\right ]^{1/n} - 1) \right ], \)
где
Распределение яркости, соответствующее формулам
При n = 4 эта формула превращается в формулу μ(r) = μe + 8,32678 [(r / re)1/4 - 1]. Из
Светимость, излучаемая в пределах расстояния r от центра галактики, равна
где
где Γ (η) = γ (η , ∞) - гамма-функция. Кривая относительной светимости:
Как несложно убедиться, при n = 4 формулы
Из определения эффективного радиуса re следует, что константа νn может быть найдена из уравнения
с относительной погрешностью ≤ 10−6. Формулы других авторов, как правило, сводятся к первым двум членам разложения
Таблица: Точные значения коэффициента νn согласно (Ciotti L., Bertin G., A&A, v.352, p.447, 1999)
| 1 | 1.67834699 |
| 2 | 3.67206075 |
| 3 | 5.67016119 |
| 4 | 7.66924944 |
| 5 | 9.66871461 |
| 6 | 11.6683632 |
| 7 | 13.6681146 |
| 8 | 15.6679295 |
| 9 | 17.6677864 |
| 10 | 19.6676724 |
Яркие эллиптические галактики хорошо описываются законом Серсика при n ~ 4, карликовые эллиптические галактики и диски спиральных галактик - при n ~ 1, а балджи и эллиптические галактики промежуточных светимостей могут быть представлены формулой
Динамические свойства закона r1/n обсуждаются в работах[2][3][4][5]
Страница: 0
Примечания[править | править код]
См. также[править | править код]
- Звезда
- Скрытая масса
- Парсек
- Красное смещение
- Масса
- Солнце
- Наблюдаемая Вселенная
- Млечный Путь
- Фотометрия
- Светимость
Ссылки[править | править код]
Закон Серсика на:
- http://ru.wikipedia.org/wiki/%D0%97%D0%B0%D0%BA%D0%BE%D0%BD_%D0%A1%D0%B5%D1%80%D1%81%D0%B8%D0%BA%D0%B0
- http://www.astronet.ru/db/msg/1166765/node14.html
- http://www.enci.ru/%D0%97%D0%B0%D0%BA%D0%BE%D0%BD_%D0%A1%D0%B5%D1%80%D1%81%D0%B8%D0%BA%D0%B0
- http://heritage.sai.msu.ru/otchet/leto2001/Koposov/Koposov3.html
- http://www.astronet.ru/db/msg/1166765/index.html