Межмолекулярное взаимодействие

Межмолекулярное взаимодействие — взаимодействие между электрически нейтральными молекулами или атомами. Силы межмолекулярного взаимодействия впервые принял во внимание Я. Д. Ван-дер-Ваальс (1873) для объяснения свойств реальных газов и жидкостей.

Природа межмолекулярного взаимодействия

Межмолекулярное взаимодействие имеет электрическую природу и складывается из сил притяжения (ориентационных, индукционных и дисперсионных) и сил отталкивания.

Ориентационные силы

Два электрических диполя ab и cd при указанном взаимном расположении притягиваются, т. к. разноимённые заряды в точках b и с взаимодействуют сильнее, чем одноимённые заряды в точках а и с (а также в b и d).

Ориентационные силы действуют между полярными молекулами, то есть обладающими дипольными электрическими моментами. Сила притяжения между двумя полярными молекулами максимальна в том случае, когда их дипольные моменты располагаются вдоль одной линии (см. рисунок). Эта сила возникает благодаря тому, что расстояния между разноимёнными зарядами немного меньше, чем между одноимёнными. В результате притяжение диполей превосходит их отталкивание. Взаимодействие диполей зависит от их взаимной ориентации, и поэтому силы дипольного взаимодействия называются ориентационными. Хаотическое тепловое движение непрерывно меняет ориентацию полярных молекул, но, как показывает расчёт, среднее по всевозможным ориентациям значение силы имеет определённую величину, не равную нулю. Потенциальная энергия ориентационного межмолекулярного взаимодействия:

$U_{op}(r)$~$\frac{p_1p_2} {r^6}$ где p₁ и p₂ — дипольные моменты взаимодействующих молекул.

Соответственно сила взаимодействия: $F_{op}$~$r^{-7}$.

Сила Fор убывает с расстоянием значительно быстрей, чем кулоновская сила взаимодействия заряженных тел (Fкул ~ r^-2).

Индукционные силы

Индукционные (или поляризационные) силы действуют между полярной и неполярной молекулами. Полярная молекула создаёт электрическое поле, которое поляризует молекулу с электрическими зарядами, равномерно распределёнными по объёму. Положительные заряды смещаются по направлению электрического поля, а отрицательные — против. В результате у неполярной молекулы индуцируется дипольный момент.

Энергия межмолекулярного взаимодействия в этом случае пропорциональна дипольному моменту p1 полярной молекулы и поляризуемости a2, характеризующей способность другой молекулы поляризоваться:

Uинд(r) ~ p1 a2 / r⁶.

Эта энергия называется индукционной, так как она появляется благодаря поляризации молекул, вызванной электростатической индукцией. Индукционные силы (Fинд ~ r ^-7) действуют также и между полярными молекулами.

Дисперсионные силы

Между неполярными молекулами действует дисперсионное межмолекулярное взаимодействие. Природа этого взаимодействия была выяснена полностью только после создания квантовой механики. В атомах и молекулах электроны сложным образом движутся вокруг ядер. В среднем по времени дипольные моменты неполярных молекул оказываются равными нулю. Но в каждый момент электроны занимают какое-то положение. Поэтому мгновенное значение дипольного момента (например, у атома водорода) отлично от нуля. Мгновенный диполь создаёт электрическое поле, поляризующее соседние молекулы. В результате возникает взаимодействие мгновенных диполей. Энергия взаимодействия между неполярными молекулами есть средний результат взаимодействия всевозможных мгновенных диполей с дипольными моментами, которые они наводят в соседних молекулах благодаря индукции. Потенциальная энергия дисперсионного межмолекулярного взаимодействия:

Uдисп(r) ~ a1a2 / r⁶ а Fдисп ~ r^-7(здесь a1 и a2 — поляризуемости взаимодействующих молекул).

Межмолекулярное взаимодействие данного типа называется дисперсионным потому, что дисперсия света в веществе определяется теми же свойствами молекул, что и это взаимодействие. Дисперсионные силы действуют между всеми атомами и молекулами, так как механизм их появления не зависит от того, есть ли у молекул (атомов) постоянные дипольные моменты или нет. Обычно эти силы превосходят по величине как ориентационные, так и индукционные. Только при взаимодействии молекул с большими дипольными моментами, например молекул воды, Fор > Pдисп (в 3 раза для молекул воды). При взаимодействии же таких полярных молекул, как CO, HI, HBr и других, дисперсионные силы в десятки и сотни раз превосходят все остальные.

Очень существенно, что все три типа межмолекулярного взаимодействия одинаковым образом убывают с расстоянием:

U = Uop + Uинд + Uдисп ~ r^-6

Силы отталкивания

Силы отталкивания действуют между молекулами на очень малых расстояниях, когда приходят в соприкосновение заполненные электронные оболочки атомов, входящих в состав молекул. Существующий в квантовой механике принцип Паули запрещает проникновение заполненных электронных оболочек друг в друга. Возникающие при этом силы отталкивания зависят в большей степени, чем силы притяжения, от индивидуальности молекул. К хорошему согласию с данными экспериментов приводит допущение, что потенциальная энергия сил отталкивания Uот возрастает с уменьшением расстояния по закону:

Uот(r) ~ r^-12, a Fот ~ r^-13.

Результирующее взаимодействие

Зависимость потенциала U(r) межмолекулярного взаимодействия Леннарда-Джонса от расстояния r между молекулами. Расстояние r = σ — наименьшее возможное расстояние между неподвижными молекулами, ε — глубина «потенциальной ямы» (энергия связи молекул).

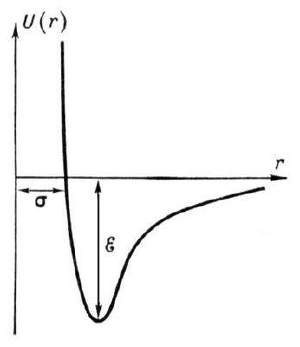
Если принять, что U(r) = 0 при r → ∞, и учесть, что энергия притяжения убывает с уменьшением расстояния пропорционально r^-6, а энергия отталкивания растет как r^-12, то кривая U(r) будет иметь вид, изображенный на рисунке. Минимуму потенциальной энергии соответствует расстояние, на котором силы взаимодействия молекул равны нулю.

Рассчитать с достаточной точностью U(r) на основе квантовой механики при огромном разнообразии пар взаимодействующих молекул практически нельзя. Не удаётся пока и экспериментально измерить силу взаимодействия на межмолекулярных расстояниях. Поэтому обычно подбирают такую формулу для U(r), чтобы проделанные с её помощью расчёты хорошо бы согласовались с экспериментом. Наиболее часто пользуются формулой:

U(r)=4ε((σ/r)¹² - (σ/r)⁶)

так называемым потенциалом Леннарда-Джонса. Входящие в формулу величины σ и ε определяются экспериментально на основе зависимости свойств веществ (например, коэффициенты диффузии, теплопроводности или вязкости) от σ и ε.

Уравнение Ван-Дер-Ваальса

Ван дер Ваальс предположил, что на малых расстояниях (r) между молекулами действуют силы отталкивания, которые с увеличением расстояния сменяются силами притяжения. На основе этих представлений, даже не рассматривая количественной зависимости межмолекулярного взаимодействия от расстояния, он получил так называемое Ван-дер-Ваальсово уравнение состояния реального газа.

См. также

• Нанотехнология