Парадокс Браеса
Честь открытия данного парадокса принадлежит немецкому математику Дитриху Браессу. Суть его сводится к тому, что добавление дополнительных возможностей к сети (компьютерной, транспортной и т. п.) при независимом («эгоистическом») распределении нагрузки на ее элементы может в некоторых случаях уменьшать эффективность ее работы, поскольку равновесие такой измененной сети не обязательно оптимальное.
Описание[править | править код]
Рассмотрим две точки Start и End (см. рис. 1), между которыми есть два пути, проходящие через точки А и В. Пропускная способность трассы Start-А равна 100 машин\мин и равна пропускной способности трассы В-End. Время, затрачиваемое машинами на прохождение этих трасс, равно n\p, где n — количество машин, проходящих по трассе, а p — пропускная способность трассы. Пропускная способность трасс А-End и Start-В не зависит от количества машин (очень мощные трассы), и среднее время прохождения машин по ним равно 45 мин.
Предположим, что 4000 машин стремятся попасть из точки Start в точку End. Каждая из них выбирает для себя наиболее оптимальный путь. В силу симметричности ситуации половина машин (2000) выберет путь Start-А-End, а другая половина — путь Start-В-End. Время, затрачиваемое ими на прохождение того и другого пути, равно 65 мин (2000\100 + 45 или 45 + 2000\100).
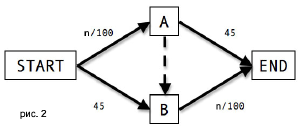
А теперь представим, что государство решило сократить это время и открыло между точками А и В дополнительную мощную одностороннюю трассу, время прохождения которой составляет всего 5 мин (см. рис. 2). Поскольку старые трассы никто не закрывает, то у водителей, теоретически, появляется дополнительный выбор. Но вот парадокс: в этой ситуации все водители выбирают путь Start-А-В-End, поскольку в своей начальной части (Start-А) он составляет всего 40 мин даже в самом худшем варианте (когда все 4000 машин устремляются по нему), тогда как путь Start-В — 45 мин. Дальше выбора опять практически нет, поскольку на путь А-В затрачивается 5 мин, а на путь В-End — опять же в самом худшем варианте — 40 мин. Разумеется, все надеются на лучший вариант (поскольку на путь А-End также затрачивается 45 мин, и есть надежда, что какие-то машины выберут его), когда хотя бы одна машина выбирает продолжение А-End. В результате все выбирают путь А-В-End, и общее время прохождения пути Start-А-В-End составляет 85 мин (4000\100 + 5 + 4000\100). То есть общее время прохождения пути между точками А и В увеличивается на 20 мин, хотя, казалось бы, новая трасса была открыта именно для уменьшения этого времени.
Но самое парадоксальное в данной ситуации заключается в том, что сократить это время можно только одним способом — закрыв вновь открытую трассу А-В и вернувшись к старой структуре транспортной сети. К примеру, если разделить машины на два потока и направить половину из них по пути Start-А-В-End, а другую половину — по пути Start-В-End, то ситуация улучшается ненамного, поскольку на прохождение первого затрачивается 65 мин, а на прохождение второго — 85 мин. В среднем получается (65 + 85)\2 = 75 мин. Казалось бы, на первый путь должно затрачиваться всего 45 мин (2000\100 + 5 + 2000\100), а на второй — 65 мин (45 + 2000\100), но здесь не учитывается то, что трасса В-End в этом случае является общей для обоих потоков машин, почему на первый путь и затрачивается 65 мин (2000\100 + 5 + 4000\100), а на второй — 85 мин (45 + 4000\100). То же самое получается, если все машины следуют сначала по трассе Start-А, а в точке А разделяются на два равных потока, один из которых следует по пути А-End, а другой — по пути А-В-End…
Решение[править | править код]
Собственно говоря, решение данного парадокса уже названо — это удаление дополнительного элемента сети и возвращение к ее прежней структуре. Такое решение называется тривиальным. Более сложная задача: анализ существующих сетей на наличие парадокса Браесса и удаление парадоксального элемента сети. Такая задача пока что не решена, поскольку не известен алгоритм, который позволял бы однозначно устанавливать указанный элемент. Или, что равносильно, устанавливать оптимальную конфигурацию сети.
Другое решение состоит в централизованном управлении потоками в сетях. Такое управление даже малой частью потока может дать значительный эффект. Проблема в том, что затраты на централизацию могут свести к нулю этот эффект и даже сделать сеть нерентабельной. Это подсказывает еще одно решение парадокса Браесса — удешевление самих элементов сети. Или, в более общем случае — оптимизация этих элементов.
Еще одно решение — это введение «платы» за прохождение элементов сети, что автоматически регулирует интенсивность проходящих через них потоков.
Примеры парадокса Браесса в жизни[править | править код]
В Сеуле в Южной Корее после удаления автомобильного пути как части проекта восстановления ручья Чонгечон стала видна неэффективность кольцевой дороги вокруг города. В Штутгарте в Германии после инвестиций в дорожную сеть в 1969 году ситуация на дорогах не улучшилась, пока не была закрыта для движения секция вновь смонтированной дороги. В 1990 году в США закрытие 42-й авеню в Нью-Йорке уменьшило перегрузку на дорогах в штате…