Шкала расстояний в астрономии
Введение[править | править код]
Шкала расстояний в астрономии — комплексное название проблем, связанных с измерением расстояний в астрономии.
Построение шкалы[править | править код]
Метод тригонометрических параллаксов[править | править код]
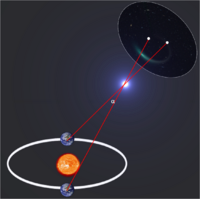
Годичный параллакс — угол, под которым виден средний радиус Земной орбиты из центра масс звезды. Существование годичного параллакса обусловлено только законами геометрии и более ничем, таким образом данный метод сродни прикладыванию линейки и является моделенезависимым. Из тех же законов геометрии искомое расстояние до звезды равно:
Однако на практике никто так не считает, т.к. параллакс - малый угол. А для малых углов sinα = α. И итоговая формула, которую и используют на практике:
- где угол α выражен в радианах. Значение параллакса уменьшается с ростом расстояния до звезды, резко ограничивая область применения метода.
Метод определения расстояния по цефеидам и звездам типа RR лиры[править | править код]
Цефеиды и звезды типа RR Лиры - переменные объекты, но если цефеиды молодые объекты, то вторые - звезды уже сошедшие с главной последовательности гиганты спектральных классов A-F. Характерной их особенностью является зависимость "Период пульсация - Абсолютная звездная величина".
Основных проблем данного метода две:
- невысокая светимость самих объектов. Т.е. крайне трудно в далекой галактике найти цефеиду;
- необходимо учитывать поглощение света пылью, как при калибровке зависимостей, так и при самих измерениях расстояний.
Метод определения расстояния по сверхновым типа Ia[править | править код]
Сверхновые типа Ia — это взрыв белого карлика в тесной двойной системе. Основываясь на расстоянии, полученном на основе измерения по цефеидам, было установлено, что все сверхновые данного типа в максимуме имеет примерно одинаковую светимость.
Физическая схема явления проста: аккрецирующее вещество со звезды-компаньона скапливается в значительном количестве на поверхности белого карлика. В какой-то момент давление вырожденного газа более не способно выдерживать вес скопившегося вещества, происходит коллапс. Масса белого карлика на тот момент известна и равна пределу Чандрасекара. Именно данный факт, по мнению теоретиков, является причиной одинаковой светимости в максимуме.
Тогда, если застать вспышку в максимуме блеска, то можно определить расстояние до сверхновой, а по линиям в спектре определить красное смещение. Следуя подобным путем, в 1998 году две группы наблюдателей открыли ускоряющееся расширение Вселенной.
Метод определения расстояния по гравитационным линзам[править | править код]
Проходя около массивного тела, луч света отклоняется. Таким образом массивное тело способно собирать параллельный пучок света в некотором фокусе, строя изображение, причем их может быть несколько. Время запаздывания между изображениями, в большинстве случаев, в первом приближении равно tdel = d / c, где d — расстояние между изображениями, а с — скорость света.
Зная угловое расстояние между изображениями и применяя законы геометрии, можно вычислить расстояние до линзы. Однако минус этого метода в том, что априори неизвестны гравитационный потенциал линзы и его структура. Связанная с этим ошибка может быть значительна для точных измерений.
Связь проблемы шкалы расстояний с ключевыми проблемами астрофизики[править | править код]
История[править | править код]
Страница: 0
Примечания[править | править код]
См. также[править | править код]
Ссылки[править | править код]
Литература[править | править код]
- Шкала расстояний во вселенной
- Игорь Дроздовский. "Методы определения расстояний до галактик".
- Расстояния до космических объектов (методы определения) // Физика космоса / под редакцией Р. А. Сюняева. — 2-е изд. — М.: Советская энциклопедия, 1986. — С. 569—573.