Тонкая линза
Тонкая линза[править | править код]
Тонкая линза — линза, когда толщина самой линзы d (расстояние между наружными точками сфер) мала по сравнению с радиусами кривизны сферических поверхностей d <<R1 и R2. В противном случае такие линзы называются толстыми.
Линзы входят в состав практически всех оптических устройств. Линзы (Рис.3) делятся на собирающие и рассеивающие.
Основные определения тонкой линзы[править | править код]
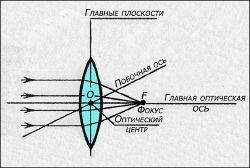
Главной оптической осью линзы (См. Рис.2) считается ось, проходящая через центры кривизны её поверхностей. В тонкой линзе точки пересечения главной оптической оси с обеими поверхностями линзы сливаются в одну точку О.(Т.к. очень большие радиусы кривизны приближаются к плоскостям, то сферические поверхности теоретически сливаются в одну плоскость ). Эта точка называется оптическим центром линзы. Тонкая линза имеет одну главную плоскость, которая общая для двух сферических поверхностей и проходит через центр призмы и перпендикулярна к главной оптической оси. Все прямые, проходящие через оптический центр линзы, называются побочными оптическими осями линзы. Важным является то, что все лучи, идущие через оптический центр линзы, не преломляются.
Если на линзу направить пучок лучей, параллельных главной оптической оси, то после прохождения через линзу лучи (или их продолжения) соберутся в одной точке F, которая называется главным фокусом линзы. У тонкой линзы имеются два главных фокуса, расположенных симметрично на главной оптической оси относительно линзы. У собирающих линз фокусы действительные, у рассеивающих – мнимые. Пучки лучей, параллельных одной из побочных оптических осей, после прохождения через линзу также фокусируются в точку F', которая расположена при пересечении побочной оси с фокальной плоскостью Ф, то есть плоскостью, перпендикулярной главной оптической оси и проходящей через главный фокус (рис. 1.1). Расстояние между оптическим центром линзы O и главным фокусом F называется фокусным расстоянием. Оно обозначаетcя той же буквой F.
Поток монохроматических параллельных лучей или пучков лучей с осями их узких конусов , нормалльных к сферической границе раздела (к главной плоскости, см.Рис.2), называют парксиальными (приосевыми) пучками. При этом, пройдя через неё сходятся в главном фокусе линзы F2. Главные фокусы линзы лежат на главной оптической оси линзы. Точки, расположенные на главной оптической оси линзы с двух сторон оптического центра на равных расстояниях f2. (См. Рис.4), называются главными фокусами линзы . Плоскости, проходящие через главные фокусы f2 линзы и перпендикулярные к её главной оптической оси, называются фокальными плоскостями линзы .
Непараксиальные пучки не дают стигматических оптических изображений и после преломления становятся не гомоцентрическими.
Формула тонкой линзы[править | править код]
Все формулы тонкой линзы смотри в:
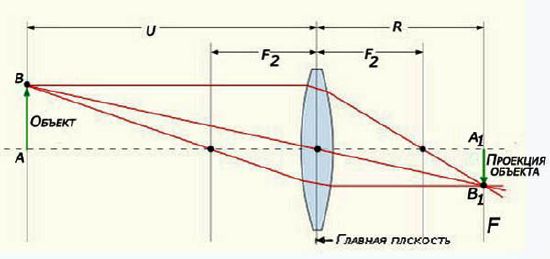
Расстояния от точки предмета до центра линзы и от точки изображения до центра линзы называются сопряжёнными фокусными расстояниями.
Эти величины находятся в зависимости между собой и определяются формулой, называемой формулой тонкой линзы:
где — расстояние от линзы до предмета; — расстояние от линзы до изображения; — главное фокусное расстояние линзы. В случае толстой линзы формула остаётся без изменения с той лишь разницей, что расстояния отсчитываются не от центра линзы, а от главных плоскостей.[1]
См. также[править | править код]
Примечания[править | править код]
- ↑ * Б. М. Яворский и А. А. Детлаф Справочник по физике. — М.: Наука, 1971.