Вынужденное излучение
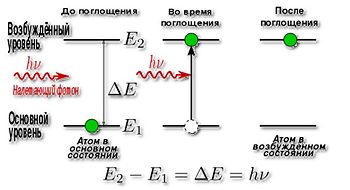
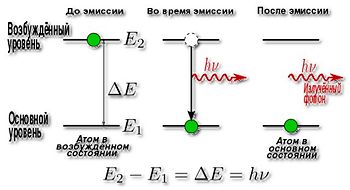
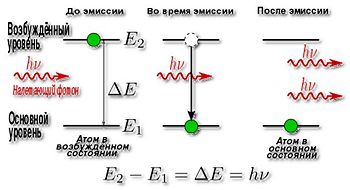
Вынужденное излучение — индуцированное излучение или испускание электромагнитных волн квантовыми системами (атома, молекулы, ядра и т. д.) под действием падающего на них излучения. При этом выполняется важное условие — лучи испускаемые сохраняют все характеристики лучей, вызывающих их излучение.
Например, фотоны испускаемые при вынужденном излучении, совпадают по частоте, направлению распространения и поляризации с фотонами, вынуждающими их испускание. (В квантовых системах (атома, молекулы, ядра и т. д. при взаимодействии с возбудителем спокойствия получаем, что с нижелажащего на вышележащеий энергетический уровень при взаимодействии с фотоном, энергия которого равна разности энергий уровней, испускается фотон с такими же энергией, импульсом, фазой и поляризацией, что и первоначальный фотон (который не поглощается). Оба фотона когерентны.) [1]
Общие сведения[править | править код]
Классическая теория излучения — теория Максвелла. Cуществование свободного электромагнитного поля, поля самоподдерживающегося не зависит от возбудивших его источников и тесно связано с электромагнитными волнами, распространяющимися от источников. Они зависят от зарядов и токов - не мгновенно, а с конечной скоростью в вакууме c = 299 792 458 м/с. Если источник излучения (например, переменный ток) в какой-то момент мгновенно исчезнет, то это не приведет к мгновенному исчезновению поля во всем пространстве. В дальних от источника точках оно исчезнет через конечный промежуток времени. Из теории Максвелла следует, что изменение во времени электрического поля Е порождает магнитное поле Н и наоборот: изменение Н порждает вихревое электрическое поле. откуда получаем, что самоподдерживающимся может быть лишь переменное электромагнитное поле, у которого обе его составлящие - Е и Н непрерывно изменяясь, постоянно возбуждая одна другую. Откуда становится понятной разница между независимым и вынужденным излучениями электромагнитных волн.[2]
Из теории Эйнштейна[править | править код]
А. Эйнштейн в теории о вынужденном излучении (испускании) внес неоценимый вклад. Его гипотеза состоит в том, что под действием электромагнитного поля частоты ω молекула (атом) может:
- перейти с более низкого энергетического уровня
- перейти с более высокого энергетического уровня
- также, как и в отсутствие возбуждающего поля, не исключается самопроизвольный переход молекулы (атома) с верхнего на нижний энергетический уровень с испусканием фотона энергией
Откуда принято:
- первый процесс называть поглощением;
- второй — вынужденным (индуцированным) испусканием;
- третий — спонтанным испусканием.
Скорость поглощения и вынужденного испускания фотона пропорциональна вероятности соответствующего перехода:
Число переходов
Связь в теории между коэффициентами[править | править код]
- В случае замкнутой полости:
- стенки её испускают и поглощают электромагнитное излучение. Такое излучение характеризуется спектральной плотностью
- стенки её испускают и поглощают электромагнитное излучение. Такое излучение характеризуется спектральной плотностью
- При термодинамическом равновесии распределение частиц по уровням энергии подчиняется закону Больцмана:
Сравнивая (4) и (5) и приняв, что
Так как при
Отличие вынужденного излучения от спонтанного[править | править код]
По свойствам вынужденное испускание существенно отличается от спонтанного:
- Наиболее характерная черта вынужденного излучения заключается в том, что возникший поток распространяется в том же направлении что и первоначальный возбуждающий поток.
- Частоты и поляризация вынужденного и первоначального излучений также равны.
- Вынужденный поток когерентен возбуждающему.
Вынужденное излучение и работа лазеров и мазеров[править | править код]
Принцип работы лазеров и мазеров основан на вынужденном излучении . В рабочем теле лазера при накачке создаётся избыточное количество атомов в верхнем энергетическом состоянии по сравнению с термодинамическим ожиданием. Рабочее тело газового лазера находится в резонаторе (в простейшем случае — пара зеркал), создающем условия для накапливания фотонов с определённым направлением импульса. Первые фотоны возникают за счёт спонтанного излучения, затем их поток лавинообразно усиливается благодаря вынужденному излучению. Лазеры обычно используются для генерации излучения, в то время как мазеры работают в области радиочастот, а также применяются для усиления.[3]
См. также[править | править код]
Ссылки[править | править код]
- ↑ http://bse.sci-lib.com/article007400.html
- ↑ Б. М. Яворский и А. А. Детлаф Справочник по физике. — М.: Наука, 1971.
- ↑ А. Л. Микаэлян, М. Л. Тер-Микаелян Ю. Г. Турков. «Оптические генераторы на твёрдом теле». М.: Советское радио, 1967.