Введение[править | править код]

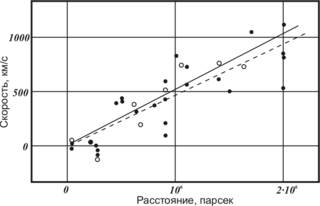
График из оригинальной работы Хаббла 1929 года

Закон Хаббла (закон всеобщего разбегания галактик) — эмпирический закон, связывающий красное смещение галактик и расстояние до них линейным образом^[1]:

c z = D H₀

Где z — красное смещение галактики, D — расстояние до нее, H₀ -коэффициент пропорциональности, называемый постоянная Хаббла. При малом значении z c z = V_r, где V_r-скорость галактики вдоль луча зрения наблюдателя, и закон принимает классический вид: $D \propto V_r.$

С помощью этого закона можно рассчитать так называемый Хаббловский возраст Вселенной (в предположении, что «разбегание» галактик действительное):

$t_H = \frac{r}{V} = \frac{1}{H_0} ,$

этот возраст с точностью до множителя 2 соответствует возрасту Вселенной, рассчитываемому по стандартной космологической модели Фридмана.

История открытия[править | править код]

Закон Хаббла установлен экспериментально Э. Хабблом в 1929 для галактик с помощью 100" телескопа, который разрешает ближайшие галактики на звезды. Среди них были цефеиды, используя зависимость «период-светимость» которых, Хаббл измерил расстояние до них, а также красное смещение.

Полученный Хабблом коэффициент пропорциональности составлял около 500 км/с на мегапарсек. Современное значение составляет 74,2 ± 3,6 км/с на мегапарсек. Столь существенную разницу обеспечивают два фактора: отсутствие поправки нуль-пункта зависимости «период-светимость» на поглощение (которое тогда ещё не было открыто) и существенный вклад собственных скоростей в общую скорость для местной группы галактик^[2].

Теоретическая интерпретация[править | править код]

С точки зрения классической механики, закон Хаббла можно наглядно объяснить следующим образом. Когда-то давно Вселенная образовалась в результате Большого взрыва. В момент взрыва различные частицы материи (осколки) получили различные скорости. Те из них, которые получили бо́льшие скорости — соответственно успели к настоящему моменту улететь дальше, чем те, которые получили меньшие скорости. Если провести численный расчёт, то окажется, что зависимость расстояния от скорости оказывается линейной. Кроме того, получается, что эта зависимость одна и та же для всех точек пространства, то есть, по наблюдениям за разлетающимися осколками нельзя найти точку взрыва: с точки зрения каждого осколка, именно он находится в центре. Однако, несмотря на такую наглядность, следует помнить, что расширение Вселенной должно описываться не классической механикой, а общей теорией относительности.

Космология

Изучаемые объекты и процессы

Наблюдаемые процессы

Теоретические изыскания

Родственные темы

Шаблон: Просмотреть·Обсудить·Изменить

Первое замечание касается того, учитывается ли при наблюдениях тот факт, что из-за того, что свет идёт от галактик миллионы лет, мы наблюдаем их в прошлом. В результате, поскольку они удаляются от нас, в настоящий момент они должны находиться уже дальше. Вопрос: для какого из двух расстояний определена зависимость Хаббла? Ответ: до середины прошлого века это не имело значения. Из графика Хаббла видно, что наибольшие скорости галактик, рассмотренных Хабблом, составили до 1000 км/с. В принципе это большая скорость, но за время движения света от них до Земли, они всё равно успели сдвинуться на незначительный процент общего расстояния.

Второе замечание заключается в том, что расширение Вселенной не является простым разлётом галактик в пустом пространстве. Оно заключается в динамическом изменении самого пространства. Непонимание этого факта часто заставляет делать неверные заключения авторов даже серьёзной литературы. Например, часто говорят, что скорость убегания галактик не должна превышать скорость света и потому на тех расстояниях, где это должно наблюдаться, должны наблюдаться и отклонения от закона Хаббла. Это не так: согласно общей теории относительности, должны существовать и наблюдаться галактики, убегающие быстрее света ^[3].

Теоретическая интерпретация[править | править код]

За несколько лет до экспериментального открытия Александром Фридманом были теоретически решены уравнения Эйнштейна для всей Вселенной и в результате было получено, что если распределение вещества в ней в среднем равномерно, то она должна или сжиматься или расширяться, причём в последнем случае должен наблюдаться линейный закон между расстоянием и скоростью убегания. Эта особенность решений Фридмана была сразу же отождествлена с явлением, открытым Хабблом.

В соответствии с этой (общепринятой) моделью космологическое красное смещение нельзя интерпретировать как Эффект Доплера, так как получаемая из наблюдаемого $z$ по формулам этого эффекта скорость не соответствует (лишь приближенно равна) никакой скорости в смысле изменения космологического расстояния между галактиками. Галактики неподвижны (за исключением пекулярных собственных скоростей), а расширяется пространство, что и вызывает расширение волнового пакета. (См. в статье Космологическое красное смещение). Так соотношение $\displaystyle cz \approx H_0D$

является приближённым, в то время как равенство $V=\frac{dD}{dt} = H_0D$

где D — расстояние в данный момент, есть точное равенство, то есть красное смещение линейно связано с расстоянием только приближённо для близких галактик, а скорость их удаления линейно возрастает с расстоянием точно. Таким образом, в последней формуле скорость $V$ не соответствует скорости, рассчитываемой по эффекту Допплера.

Оценка постоянной Хаббла и её физический смысл[править | править код]

В процессе расширения, если оно происходит равномерно, постоянная Хаббла должна уменьшаться, и индекс «0» при её обозначении указывает на то, что величина Н₀ относится к современной эпохе. Величина, обратная постоянной Хаббла должна быть в таком случае равна времени, прошедшему с момента начала расширения, то есть, возрасту Вселенной.

Значение Н₀ определяется по наблюдениям галактик, расстояния до которых измерены без помощи красного смещения (прежде всего, по ярчайшим звёздам или цефеидам). Большинство независимых оценок Н₀ дают для этого параметра значение 70—80 км/с на мегапарсек. Это означает, что галактики, находящиеся на расстоянии 100 мегапарсек, удаляются от нас со скоростью 7000—8000 км/с. В настоящее время (2009) наиболее надёжной (хотя и модельно зависимой) считается оценка Н₀=(74,2 ± 3,6) км/с/Мпк.

Проблема оценки Н₀ осложняется тем, что, помимо космологических скоростей, обусловленных расширением Вселенной, галактики ещё обладают собственными (пекулярными) скоростями, которые могут составлять несколько сотен км/с (для членов массивных скоплений галактик — более 1000 км/с). Это приводит к тому, что закон Хаббла плохо выполняется или совсем не выполняется для объектов, находящихся на расстоянии ближе 10-15 млн св. лет, то есть как раз для тех галактик, расстояния до которых наиболее надёжно определяются без красного смещения.

Закон Хаббла плохо выполняется и для галактик на очень больших расстояниях (в миллиарды св. лет), которым соответствует величина z > 1. Расстояния до объектов с таким большим красным смещением теряют однозначность, поскольку зависят от принимаемой модели Вселенной и от того, к какому моменту времени они отнесены. В качестве меры расстояния в этом случае обычно используется только красное смещение.

Возможная нелинейность закона[править | править код]

В наше время наблюдениями, говорящими в пользу существования тёмной энергии, были, по-видимому, обнаружены отклонения от линейного закона Хаббла (как связи красного смещения с расстоянием). Было обнаружено, по-видимому, что наша Вселенная расширяется с ускорением. Этот факт не отменяет закона Хаббла, так как последний действует на более близких расстояниях, чем эти новые эффекты.

Страница: 0

en Hubble's law