Основы функционального программирования/Структуры данных и базисные операции

Лекции по функциональному программированию

1. Вводная лекция 2. Структуры данных и базисные операции 3. Структуры данных и базисные операции — 2 4. Основы языка Haskell 5. Служебные слова и синтаксис Haskell'а 6. Модули и монады в Haskell'е 7. Операции ввода/вывода в Haskell'е 8. Конструирование функций 9. Доказательство свойств функций 10. Формализация ФП на основе λ-исчисления 11. Трансформация программ

Введение

Как уже́ говорилось в первой лекции, основой функциональной парадигмы программирования в большей мере являются такие направления развития математической мысли, как комбинаторная логика и λ-исчисление. В свою очередь последнее более тесно связано с функциональным программированием, и именно λ-исчисление называют теоретическими основами функционального программирования.

Для того, чтобы рассматривать теоретические основы функционального программирования, необходимо в первую очередь ввести некоторые соглашения, описа́ть обозначения и построить некоторую формальную систему.

Пусть заданы объекты некоторого первичного типа $A$. Сейчас совершенно не важно, что именно представляют собой эти выделенные объекты. Обычно считается, что на этих объектах определён набор базисных операций и предикатов. По традиции, которая пошла ещё от МакКарти (автор Lisp’а), такие объекты называются атомами. В теории фактический способ реализации базисных операций и предикатов совершенно не важен, их существование просто постулируется. Поэтому каждый конкретный функциональный язык реализует базисный набор по-своему.

В качестве базисных операций традиционно (и в первую очередь это объясняется теоретической необходимостью) выделяются следующие три:

1. Операция создания пары — $prefix(x,y) \equiv x:y \equiv [x \mid y]$. Эта операция также называется конструктором или составителем.
2. Операция отсечения головы — $head(x) \equiv h(x)$. Это первая селективная операция.
3. Операция отсечения хвоста — $tail(x) \equiv t(x)$. Это вторая селективная операция.

Селективные операции отсечения головы и хвоста также называют просто селекторами. Выделенные операции связаны друг с другом следующими тремя аксиомами:

1. $head(x:y) = x$
2. $tail(x:y) = y$
3. $prefix(head(x:y), tail(x:y)) = (x:y)$

Всё множество объектов, которые можно сконструировать из объектов первичного типа в результате произвольного применения базисных операций, носит название множество $S$-выражений (обозначение — $SExpr(A)$). Например:

$a_{1}:(a_{2}:a_{3}) \in SExpr(A)$

Для дальнейших исследований вводится фиксированный атом, который также принадлежит первичному типу $A$. Этот атом в дальнейшем будет называться «пустым списком» и обозначаться символами $[]$ (хотя в разных языках функционального програмирования могут существовать свои обозначения для пустого списка). Теперь можно определить то, чем собственно занимается функциональное программирование — собственное подмножество $List(A) \subset SExpr(A)$, которое называется «список над $A$».

Определение:

1. Пустой список $[] \in List(A)$
2. $x \in A \and y \in List(A) \Rightarrow x : y \in List(A)$

Главное свойство списка: $x \in List(A) \and x \neq [] \Rightarrow head(x) \in A, tail(x) \in List(A)$.

Для обозначения списка из $n$ элементов можно употреблять множество различных нотаций, однако здесь будет использоваться только такая: $[a_{1}, a_{2}, \ldots, a_{n}]$. Применяя к такому списку определённым образом операции $head$ и $tail$ можно добраться до любого элемента списка, т. к.:

$head([a_{1}, a_{2}, \ldots, a_{n}]) = a_{1}$

$tail([a_{1}, a_{2}, \ldots, a_{n}]) = [a_{2}, \ldots, a_{n}]$ (при $n > 0$).

Кроме списков вводится ещё один тип данных, который носит название «списочная структура над $A$» (обозначение — $ListStr(A)$), при этом можно построить следющую структуру отношений: $List(A) \subset ListStr(A) \subset SExpr(A)$. Определение списочной структуры выглядит следующим образом:

Определение:

1. $a \in A \Rightarrow a \in ListStr(A)$.
2. $List(ListStr(A)) \in ListStr(A)$.

Т. е. видно, что списочная структура — это список, элементами которого могут быть как атомы, так и другие списочные структуры, в том числе и обыкновенные списки. Примером списочной структуры, которая в тоже время не является простым списком, может служить следующее выражение: $[a_{1}, [a_{2}, a_{3}, [a_{4}]], a_{5}]$. Для списочных структур вводится такое понятие, как уровень вложенности.

Несколько слов о программной реализации

Пришло время уделить некоторое внимание рассмотрению программной реализации списков и списочных структур. Это необходимо для более тонкого понимания того, что происходит во время работы функциональной программы, как на каком-либо реализованном функциональном языке, так и на абстрактном языке.

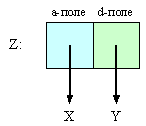
Каждый объект занимает в памяти машины какое-то место. Однако атомы представляют собой указатели (адреса) на ячейки, в которых содержатся объекты. В этом случае пара $z = x:y$ графически может быть представлена так, как показано на рисунке 1.

Рисунок 1. Представление пары в памяти компьютера

Адрес ячейки, которая содержит указатели на $x$ и $y$, и есть объект $z$. Как видно на рисунке, пара представлена двумя адресами — указатель на голову и указатель на хвост. Традиционно первый указатель (на рисунке выделен голубым цветом) называется a-поле, а второй указатель (на рисунке — зеленоватый) называется d-поле.

Для удобства представления объекты, на которые указывают a- и d-поля, в дальнейшем будут записываться непосредственно в сами поля. Пустой список будет обозначаться перечёркнутым квадратом (указатель ни на что не указывает).

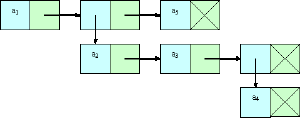
Таким образом, списочная структура, которая рассмотрена несколькими параграфами ранее ($[a_{1}, [a_{2}, a_{3}, [a_{4}]], a_{5}]$) может быть представлена так, как показано на рисунке 2.

Рисунок 2. Графическое представление списочной структуры [a1, [a2, a3, [a4] ], a5]

На этом рисунке также хорошо проиллюстрировано понятие уровня вложенности — атомы $a_{1}$ и $a_{5}$ имеют уровень вложенности 1, атомы $a_{2}$ и $a_{3}$ — 2, а атом $a_{4}$ — 3 соответственно.

Остается отметить, что операция $prefix$ требует расхода памяти, ибо при конструировании пары выделяется память под указатели. С другой стороны обе операции $head$ и $tail$ не требуют памяти, они просто возвращают адрес, который содержится соответственно в a- или d-поле.

Примеры

Пример 5. Операция $prefix$.

Для начала необходимо рассмотреть более подробно работу операции $prefix$. Пояснение работы будет проведено на трёх более или менее общих примерах:

1. $prefix(a_{1}, a_{2}) = a_{1}:a_{2}$ (при этом результат не является элементом $ListStr(A)$).
2. $prefix(a_{1}, [b_{1}, b_{2}]) = [a_{1}, b_{1}, b_{2}]$
3. $prefix([a_{1}, a_{2}], [b_{1}, b_{2}]) = [[a_{1}, a_{2}], b_{1}, b_{2}]$

Пример 6. Функция определения длины списка $length$.

Перед тем, как собственно начать реализовывать функцию $length$, необходимо понять, что она должна возвращать. Понятийное определение результата функции $length$ может звучать как «количество элементов в списке, который передан функции в качестве параметра». Здесь возникает два случая — функции передан пустой список и функции передан непустой список. С первым случаем всё ясно — результат должен быть нулевым. Во втором случае задачу можно разбить на две подзадачи, путём разделения переданного списка на голову и хвост при помощи операций $head$ и $tail$.

Осмысленно, что операция $head$ возвращает первый элемент списка, а операция $tail$ возвращает список из оставшихся элементов. Пусть известна длина списка, полученного при помощи операции $tail$, тогда длина исходного списка будет равна известной длине, увеличенной на единицу. В этом случае можно легко записать определение самой функции $length$:

$length([]) = 0$

$length(L) = 1 + length (tail(L))$

Пример 7. Функция слияния двух списков $append$.

Реализовать функцию слияния (или сцепления) списков можно многими способами. Первое, что приходит в голову — деструктивное присваивание. Т. е. заменить указатель на $[]$ в конце первого списка на указатель на голову второго списка и тем самым получить результат в первом списке. Однако здесь изменяется сам первый список. Такие приёмы запрещены в функциональном программировании (хотя, в очередной раз необходимо заметить, что в некоторых функциональных языках всё-таки есть такая возможность).

Второй способ состоит в копировании верхнего уровня первого списка и помещении в последний указатель копии ссылку на первый элемент второго списка. Этот способ хорош с точки зрения деструктивности (не выполняет деструктивных и побочных действий), однако требует дополнительных затрат памяти и времени.

$append([], L_{2}) = L_{2}$

$append(L_{1}, L_{2}) = prefix(head(L_{1}), append(tail(L_{1}), L_{2}))$

Последний пример показывает, как при помощи постепенного конструирования можно построить новый список, который равен сцепке двух заданных.

Упражнения

1. Построить функции, вычисляющие $N$-ый элемент следующих рядов:
   1. $a_{n} = x^{n}$
   2. $a_{n} = \sum_{i = 1}^{n} i$
   3. $a_{n} = \sum_{j = 1}^{n} (\sum_{i = 1}^{j} i)$
   4. $a_{n} = \sum_{i = 1}^{p} n^{-i}$
   5. $a_{n} = e^{n} = \sum_{i = 0}^{\infty} \frac{n^{i}}{i!}$
2. Объяснить результаты операции $prefix$, показанные в примере 5. Для объяснения можно воспользоваться графическим методом.
3. Объяснить результат работы функции $append$ (пример 7). Пояснить, почему функция не является деструктивной.
4. Построить функции, работающие со списками:
   1. $getN$ — функция вычленения $N$-ого элемента из заданного списка.
   2. $listSumm$ — функция сложения элементов двух списков. Возвращает список, составленный из сумм элементов списков-параметров. Учесть, что переданные списки могут быть разной длины.
   3. $oddEven$ — функция перестановки местами соседних чётных и нечётных элементов в заданном списке.
   4. $reverse$ — функция, обращающая список (первый элемент списка становится последним, второй — предпоследним, и так далее до последнего элемента).
   5. $map$ — функция применения другой переданной в качестве параметра функции ко всем элементам заданного списка.

Ответы для самопроверки

Большинство ответов для самопроверки представляют собой лишь одни из возможных вариантов (в большинстве случаев наиболее интуитивные).

1. Функции, вычисляющие $N$-ый элемент рядов:
   1. $power$:
      • $power(x, 0) = 1$
      • $power(x, n) = x * power(x, n - 1)$
   2. $summT$:
      • $summT(1) = 1$
      • $summT(n) = n + summT (n - 1)$
   3. $summP$:
      • $summP(1) = 1$
      • $summP(n) = summT(n) + summP (n - 1)$
   4. $summPower$:
      • $summPower(n, 0) = 1$
      • $summPower(n, p) = (\frac{1}{power(n, p)}) + summPower(n, p - 1)$
   5. $exponent$:
      • $exponent(n, 0) = 1$
      • $exponent(n, p) = \frac{power(n, p)}{factorial(p)} + exponent(n, p - 1)$
      • $factorial(0) = 1$
      • $factorial(n) = n * factorial(n - 1)$
2. Объяснение работы операции $prefix$ можно легко провести в три приёма (равно так же, как и приведено в примере). Для того чтобы не загромождать объяснения, здесь наряду с функциональной записью операции $prefix$ также используется инфиксная запись посредством символа двоеточия.
   1. Первый пример работы операции — определение самой операции. Рассматривать его нет смысла, ибо операция $prefix$ определяется именно таким образом.
   2. $prefix(a_{1}, [b_{1}, b_{2}]) = prefix(a_{1}, b_{1}:(b_{2}:[])) = a_{1}:(b_{1}:(b_{2}:[])) = [a_{1}, b_{1}, b_{2}]$ (Эти преобразование проведены по определению списка).
   3. $prefix([a_{1}, a_{2}], [b_{1}, b_{2}]) = prefix([a_{1}, a_{2}], b_{1}:(b_{2}:[])) = ([a_{1}, a_{2}]):(b_{1}:(b_{2}:[])) = [[a_{1}, a_{2}], b_{1}, b_{2}]$.
   4. В качестве примера работы функции $append$ рассмотрим сцепку двух списков, каждый из которых состоит из двух элементов: $[a, b]$ и $[c, d]$. Опять же для того, чтобы не загромождать объяснение, для записи операции $prefix$ используется инфиксная форма. Для более полного понимания приведённого объяснения необходимо помнить определение списка.
      • $append([a, b], [c, d]) = a:append([b], [c, d]) = a:(b:append([], [c, d])) = a:(b:([c, d])) = a:(b:(c:(d:[]))) = [a, b, c, d]$.
3. Функции, работающие со списками:
   1. $getN$:
      • $getN(n, []) = \_$
      • $getN(1, L) = head(L)$
      • $getN(n, L) = getN(n - 1, tail(L))$
   2. $listSumm$:
      • $listSumm([], L) = L$
      • $listSumm(L, []) = L$
      • $listSumm(L_{1}, L_{2}) = prefix((head(L_{1}) + head(L_{2})), listSumm(tail(L_{1}), tail(L_{2})))$
   3. $oddEven$:
      • $oddEven([]) = []$
      • $oddEven([x]) = [x]$
      • $oddEven(L) = prefix(prefix(head(tail(L)), head(L)), pddEven(tail(L)))$
   4. $reverse$:
      • $reverse([]) = []$
      • $reverse(L) = append(reverse(tail(L)), [head(L)])$
   5. $map$:
      • $map(f, []) = []$
      • $map(f, L) = prefix(f(head(L)), map(f, tail(L)))$