Параксиальная геометрическая оптика

Параксиальная геометрическая оптика

Рис.1,Схема тонкой линзы

Рис.2

Рис.3,Схема преломления лучей по Снеллу

Параксиальная геометрическая оптика — или оптика первого порядка, когда поток монохроматических параллельных лучей или пучков лучей с осями их узких конусов , нормальных к границе раздела сфер тонкой линзы (к главной плоскости, см.Рис.1), называют Параксиальными (приосевыми) пучками. При этом, пройдя через неё они сходятся в главном фокусе линзы F. Главные фокусы линзы лежат на главной оптической оси линзы. Точки, расположенные на главной оптической оси линзы с двух сторон оптического центра на равных расстояниях f₂. (См. Рис.2), называются главными фокусами линзы . Плоскости, проходящие через главные фокусы f₂ линзы и перпендикулярные к её главной оптической оси, называются фокальными плоскостями линзы .

Когда две среды разделены сферической формой раздела, то параксиальный пучок лучей после преломления называется гомоцентрическим в том случае, если угол раствора гомоцентрического пучка мал и расстояния f₂ (см. Рис.2) равны.

Непараксиальные пучки не дают стигматических оптических изображений и после преломления становятся не гомоцентрическими..

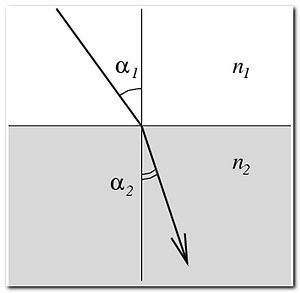
Предполагается, что линзы имеют аксиальную симметрию относительно прямой — оптической оси. Согласно закону Снелла для малых углов падения лучей (параллельных) получаем (см. Рис.3):

Угол падения света на поверхность связан с углом преломления соотношением $$n_1 \sin \alpha_1 = n_2 \sin \alpha_2\,$$

Здесь:

• $n_1$ — коэффициент преломления среды, из которой свет падает на границу раздела;
• $\alpha_1$ — угол падения света — угол между падающим на поверхность лучом и нормалью к поверхности;
• $n_2$ — коэффициент преломления среды, в которую свет попадает, пройдя границу раздела;
• $\alpha_2$ — угол преломления света — угол между прошедшим через поверхность лучом и нормалью к поверхности.

Если $n_1 \sin \alpha_1 > n_2\,$, имеет место полное внутреннее отражение (преломлённый луч отсутствует, падающий луч полностью отражается от границы раздела сред).

Формирование изображений

Рис.4, Cхема работы параксиальной геометрической оптики

В современных оптических устройствах (например, объективах — анастигматах с набором линз с коэффициентами преломления примерно n = 1,5 — 3,2 и многослойными просветляющими покрытиями) отражение световых лучей ничтожно мало и оно составляет всего 0,01-0,04%.

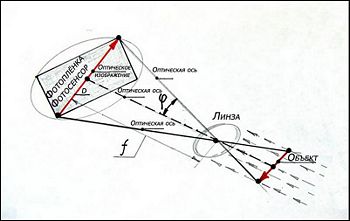
На Рис.4 на примере тонкой линзы показан ход лучей, проходящих через сферическую поверхность, расположенных нормально к главной плоскости сферических поверхностей, без преломления. Лучи, параллельные оптической оси, собираются в фокусе. При этом фронт зрения камеры равен 2φ, f — фокусное расстояние, D — диаметр фотодатчика (фотосенсора, фотоплёнки). При этом, если f меньше D, имеет место большее 2φ, т.е. рассматриваем широкоугольный анастигмат; а если f больше D, имеем малое 2φ, т.е. получаем телеобъектив.

См. также

• Тонкая линза
• Линза
• Геометрическая оптика
• Волновая оптика
• Фокальная поверхность