Параллельные прямые

В евклидовой геометрии

Параллельными (иногда — равнобежными) прямыми называются прямые, которые лежат в одной плоскости и либо совпадают, либо не пересекаются. (В некоторых школьных определениях совпадающие прямые не считаются параллельными, здесь такое определение не рассматривается).
В свою очередь, существование непересекающихся в плоскости прямых является фактом абсолютной геометрии, т.е. фактом, который может быть доказан и без использования аксиомы Евклида, и без использования аксиомы Лобачевского. А именно, верно следующее утверждение: Если две прямые (в плоскости) перпендикулярны третьей, то они не пересекаются. В планиметрии Евклида любые непересекающиеся прямые — параллельны, в планиметрии Лобачевского это не так.

Через любую точку можно провести ровно одну прямую, параллельную данной. Это отличительное свойство евклидовой геометрии, в других геометриях число 1 заменено другими (в геометрии Лобачевского таких прямых минимум две).

Используя аксиоматику Вейля и векторный подход для построения Евклидовой геометрии, параллельность прямых можно определить так: Две прямые называются параллельными, если направляющие их векторы коллинеарны.

Основные теоремы о параллельных прямых

1. Параллельность — бинарное отношение эквивалентности, поэтому разбивает всё множество прямых на классы параллельных между собой прямых.
2. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.
3. Если прямая пересекает одну из двух параллельных прямых и лежит с ними в одной плоскости (такая прямая называется секущей), то
   1. она пересекает и другую прямую.
   2. При пересечении образуется 8 углов, некоторые характерные пары которых имеют особые названия и свойства:
      1. Накрест лежащие углы равны.
      2. Соответственные углы равны.
      3. Односторонние углы в сумме составляют 180°.

В геометрии Лобачевского

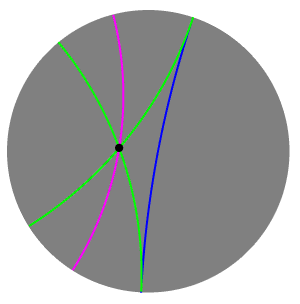
В геометрии Лобачевского в плоскости через точку $C$ вне данной прямой $a$ проходит бесконечное множество прямых, не пересекающих $a$. Из них параллельными к $a$ называются только две. Прямые $b$ и $c$ называются параллельными прямой $a$, если:

1. $b$ и $c$ не пересекают прямой $a$.
2. любая прямая, лежащая в одной паре вертикальных углов с вершиной A и образованных $b$ и $c$ пересекает $a$.
3. любая прямая, лежащая в другой паре вертикальных углов с вершиной и образованных $b$ и $c$ не пересекает $a$. В последнем случае говорят, что прямые являются расходящимися (или ультрапараллельными).

В геометрии Лобачевского кроме понятия параллельных прямых, существует и понятие направленной параллельности:
Прямая $CE$ называется параллельной (равнобежной) прямой $AB$ в направлении от $A$ к $B$, если:

1. точки $B$ и $E$ лежат по одну сторону от прямой $AC$;
2. прямая $CE$ не пересекает прямую $AB$, но всякий луч, проходящий внутри угла $ACE$, пересекает луч $AB$.

Аналогично определяется прямая, параллельной $AB$ в направлении от $B$ к $A$.

Параллельные прямые в модели Пуанкаре: две зелёные прямые параллельны синей прямой, а фиолетовая ультрапараллельна к ней

Основные теоремы о параллельных прямых

• Отношение параллельности на множестве ненаправленных прямых не является бинарным отношением эквивалентности.
• На множестве направленных прямых:
  1. через точку C, не лежащую на данной прямой, проходит одна и только одна направленная прямая, параллельная данной.
• Отношение параллельности на множестве направленных прямых есть бинарное отношение эквивалентности.
• Пусть через точку $A$, не лежащей на прямой $a$ проведена прямая $p$, параллельная $a$. Опустим из точки $A$ перпендикуляр AB к прямой $a$. Тогда:
  1. один из смежных углов $PAB$ или $PAE$ острый (пусть для определённости это будет угол $PAE$, обозначим его π — см.рисунок)
     

     $A \in p,\, p\|a,\, AB \perp a,\,AB=x$

     ---

     $\angle PAB < 90^\circ,\,\angle PAB=\pi (x),$$\pi (x)=2\operatorname{{arctg}}\ e^{-{x \over k}}$
  2. мера угла π является функцией, зависящей от длины перпендикуляра AB и вычисляется по формуле π(x)=2$\operatorname{{arctg}}\ e^{-{x \over k}}$, где x — длина перпендикуляра, а k — константа, называемая кривизной поверхности.