Характеристическая скорость орбитального манёвра
(перенаправлено с «Характеристическая скорость»)
Перейти к навигации
Перейти к поиску
| Характеристическая скорость орбитального манёвра Δv
|
- Теория:
- Астродинамика
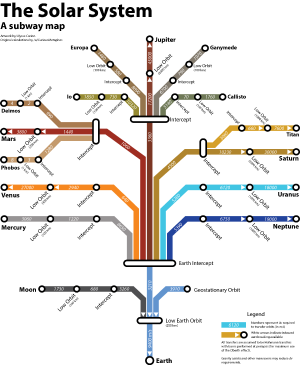
Карта-схема Солнечной системы, сделанная по образцу схемы метро, с указанием харатеристических скоростей, нужных для достижения разных тел системы. Улисс Карлон
Характеристическая скорость орбитального манёвра — в астродинамике, изменение скорости, необходимое для выполнения орбитального маневра.
Характеристическая скорость — скаляр с размерностью скорости, обозначаемый . где и — время начала и окончания манёвра, и — сила тяги двигателя и масса космического аппарата в момент .
В частности, в отсутствие внешних сил, , где — ускорение.
Для реактивного двигателя, , где — удельный импульс (теоретически, скорость истечения), а — расход реактивной массы.
Подставив эти величины в формулу характеристической скорости, получим: где и — масса аппарата в начале и конце манёвра. Если считать удельный импульс постоянным, то интегрирование даст уравнение Циолковского:
См. также[править | править код]