Эффект бабочки

Аттрактор в двумерном фазовом пространстве

Эффект бабочки — эффект, заключающийся в весьма чувствительной зависимости системы от начальных условий (в теории хаоса). Малые изменения в начальных условиях (входных параметрах) нелинейной динамической системы могут повлечь огромные изменения в долгосрочном поведении системы. В качестве примера можно привести мяч, поставленный на вершину холма, который может скатиться в любую сторону, в зависимости от мельчайших различий в начальных условиях.

Словосочетание, ставшее наименованием описываемого эффекта, описывает идею о том, что крылья бабочки могут создать мельчайшие изменения в атмосфере Земли, которые могут повлечь за собой возникновение торнадо (или наоборот предотвратить появление торнадо). взмах крыльев бабочки представляет собой мельчайшее изменение в начальных условиях системы, которое влечёт за собой цепную реакцию событий, приводящих к явлению огромного масштаба. Если бы бабочка не взмахнула крыльями, система могла бы идти по совершенно иной траектории в своём развитии.

Рекуррентность, приблизительная обратная связь системы по отношению к начальным условиям, а также высокая чувствительность к изменениям начальных условий — ингредиенты хаотичного развития. Они имеют практическую важность при исследовании сложных систем, таких как погода. Поведение таких систем сложно предсказывать в долгосрочном периоде (например, для погоды пороговым значеним длительности предсказания является примерно недельный срок).

История[править | править код]

Анимационная иллюстрация, показывающая эффект бабочки в аттракторе Лоренца: две траектории (синяя и жёлтая) начинаются в точках, которые лежат друг от друга на расстоянии

10^{-5}

. Эти траектории вначале весьма близки друг к другу, но после некоторого времени резко расходятся

Чувствительная зависимость поведения системы от начальных условий в литературк впервые была описана Ж. Адамаром в 1890 году^[1]. В 1906 году уже П. Дьюи в своей книге популяризовал этот эффект. По всей видимости, идея о том, что именно бабочка может повлиять на далеко идущие последствия посредством наращивания последовательных событий, появилась в 1952 году в коротком рассказе Р. Бредбери о путешествиях во времени (рассказ «И грянул гром», по которому в настоящее время снят художественный фильм). Но само выражение «эффект бабочки» впервые появилось в работе Э. Лоренца.

В 1961 году Лоренц использовал цифровую компьютерную модель для предсказания погоды. Во время эксперимента он ввёл начальное значение одного из параметров в виде $0.506$ вместо полного $0.506127$ , которое приводило к зависанию компьютера. В результате вместо ожидаемого был получен совершенно иной сценарий погоды^[2]. Лоренц опубликовал полученные результаты в 1963 году в статье для Академии Наук Нью-Йорка, в которой отметил, что «Один метеоролог отметил, что если теория корректна, то взмах крыльев чайки может изменить направление развития погоды». Более поздние статьи и доклады Лоренца на эту тему использовали более поэтичный образ бабочки. В соответствии со словами Лоренца на 139-й конференции Американской Ассоциации по продвижению науки в 1972 году Ф. Мерилиз придумал в качестве заголовка для своей статьи фразу «Создаёт ли взмах крыльев бабочки в Бразилии торнадо в Техасе?»

Иллюстрация[править | править код]

Эффект бабочки в аттракторе Лоренца
время $0 \leq t \leq 30$		координата $z$

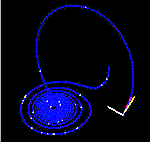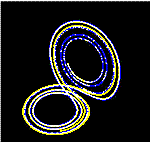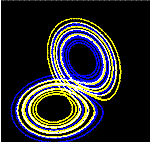
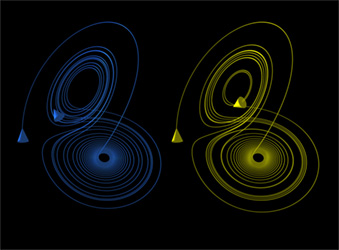
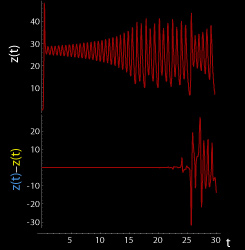
Эти фигуры показывают два сегмента трёхмерной эволюции двух траекторий (одна показана синим цветом, другая — жёлтым) для одного и того же периода времени в аттракторе Лоренца. Указанные траектории начинаются в точках, которые различаются друг от друга по координате $x$ на $10^{-5}$ . Вначале обе траектории выглядят согласованными, что показано совершенно незначительной разничей по координате $z$ , но при $t > 23$ разница между траекториями становится сравнимой с размером самих траекторий. Окончательное положение при $t = 30$ показывает, что между траекториями нет ничего общего.
Анимация на языке Java аттрактора Лоренца иллюстрирует непрерывную эволюцию.

Математическое определение[править | править код]

Динамическая система с эволюционным отображением $f^t$ показывает чувствительную зависимость от начальных условий в случае, если произвольные близлежащие элементы становятся удалёнными друг от друга с увеличением времени $t$ . Если $M$ является стартовым пространством для отображения $f^t$ , то $f^t$ показывает чувствительную зависимость от начальных условий в том случае, если существует $\delta > 0$ такая, что для каждой точки $x \in M$ и её окружения $N$ , содержащего $x$ , существует точка $y$ из этого окружения $N$ и время $\tau$ такое, что расстояние $d (f^\tau(x), f^\tau(y)) > \delta$ .

Это определение не требует того, что все точки из окружения $N$ отделены от базовой точки $x$ .

Использование в художественных произведениях[править | править код]

Концепция эффекта бабочки иногда используется в художественных произведениях совместно с идеей путешествий во времени (обычно не совсем правильно). Большинство описаний путешествий во времени не могут использовать эффект бабочки. В соответствии с теорией, если история может быть «изменена» (таким образом, что изменяющий не затрагивает нечто навроде принципа самодостаточности Новикова, что подразумевает использование самодостаточной шкалы времени), само присутствие путешенственников в прошлом является достаточным для изменения краткосрочных событий (таких, как погода), что также приведёт к непредсказуемому влиянию на отдалённое будущее. Поэтому путешественник никак не может вернуться в ту же самую версию реальности, из которой он прибыл, а потому не может путешествовать во времени. Это противоречие известно как парадокс времени.

Литература[править | править код]

Introduction to Chaotic Dynamical Systems. — Westview Press, 2003. — ISBN 0-8133-4085-3^{о книге}Регулярное выражение «ISBN» классифицировало значение «ISBN0813340853» как недопустимое.
Robert C. Hilborn (2004). "Sea gulls, butterflies, and grasshoppers: A brief history of the butterfly effect in nonlinear dynamics". American Journal of Physics 72: 425—427.

См. также[править | править код]

Примечания[править | править код]

↑ http://www.wolframscience.com/reference/notes/971c
↑ Mathis N. Storm Warning: The Story of a Killer Tornado. Touchstone, 2007. ISBN 0-7432-8053-2

Посему можно сделать вывод, что вообщем не сойдет от взмахов бабочки, и топота ног слона со своей орбиты планета Земля, и ее траектория не изменится. Тем более, что вся живая материя воздействует одна на другую на Земле, сбалансированно компенсируя силу воздействия одна другой. Потому что есть предопределенные общие космические движения некоторой космической материи по своим орбитам, и есть неопределенность действий при этом живой биосферы Земли, а вот метеориты допустим возможно могут или упасть на Землю, либо наоборот этого не сделать, от воздействия оказываемого на них Земной биосферой, но если они и упадут, то в какой либо непредсказуемой точке координат на поверерхности Земли из-за постоянного биосферного воздействия оказываемого на них.

[1] ttp://www.wolframscience.com/reference/notes/971c

[2] Mathis N. Storm Warning: The Story of a Killer Tornado. Touchstone, 2007. ISBN 0-7432-8053-2

[1]

[2]