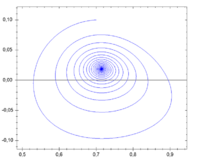
Фазовое пространство
Фазовое пространство в математике и физике представляет множество всех состояний системы в фиксированный момент времени. Каждому возможному состоянию системы соответствует точка фазового пространства.
Сущность понятия фазового пространства заключается в том, что состояние сколь угодно сложной системы представляется в нём одной единственной точкой, а эволюция этой системы — перемещением этой точки. Кроме того, в механике движение этой точки определяется сравнительно простыми уравнениями Гамильтона, анализ которых позволяет делать заключения о поведении сложных механических систем.
Механические системы[править | править код]
В случае механических систем это пространство четной размерности, координатами в котором являются обычные пространственные координаты (или обобщённые координаты) частиц системы и их импульсы (или обобщённые импульсы).
Например, фазовое пространство для системы, состоящей из одной свободной материальной точки, имеет 6 измерений, три из которых — это три обычные координаты, а ещё три — это компоненты импульса. Соответственно, фазовое пространство для системы из двух свободных материальных точек будет содержать 12 измерений и т. д.
Динамические системы[править | править код]
В теории динамических систем и теории дифференциальных уравнений фазовое пространство является более общим понятием. Оно не обязательно чётномерно и динамика на нём не обязательно задаётся уравнениями Гамильтона.
Случай нескольких систем[править | править код]
Если взять в рассмотрение несколько одинаковых систем, нужно задать несколько точек в фазовом пространстве. Совокупность таких систем называют статистическим ансамблем. По теореме Лиувилля, если точки образуют замкнутый контур, а система является Гамильтоновой, то площадь контура не меняется во времени.
Примеры[править | править код]

|
Этот раздел ещё не написан. Согласно замыслу одного из участников «Традиции», на этом месте должен располагаться раздел, посвящённый термодинамике и квантовой механике (текст можно взять из английской статьи). Надо затронуть и синергетику и такие прикладные направления, как анализ размерности (им занимался ещё Н. А. Морозов более ста лет тому назад). Примеры надо написать доступным языком. Без них статья показывает очаровательное явление под названием «Сферический конь в вакууме». Вы можете помочь проекту, написав этот раздел. |