Графен
| Графен | |
|---|---|
| |
| Структура | |
| Кристаллическая структура | Гексагональная решётка[1] |
| Постоянная решётки | 0,246 нм[1] |
| Электронные свойства | |
| Эффективная масса электронов | 0 me[2] |
| Эффективная масса дырок | 0 me[2] |
|
Зонная структура | |
| Ширина запрещённой зоны | 0 эВ[1] |
Графе́н (англ. graphene) — слой атомов углерода, соединённых посредством sp² связей в гексагональную двумерную кристаллическую решётку и одна из аллотропных форм углерода.
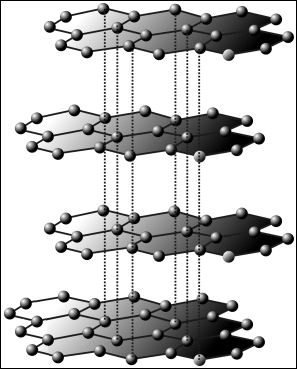
Его можно представить как одну плоскость графита, отделённую от объёмного кристалла. По оценкам графен обладает большой механической жесткостью и хорошей теплопроводностью (~1 ТПа и 3×103 Вт2м−1K−1 соответственно[3]). Хорошая электрическая проводимость делает его перспективным материалом для использования в самых различных приложениях, в частности, как будущую основу наноэлектроники[4] и возможную замену кремния в интегральных микросхемах.
Основной из существующих в настоящее время способов получения графена[2][5] основан на механическом отщеплении или отшелушивании слоёв графита. Он позволяет получать наиболее качественные образцы с высокой подвижностью носителей. Этот метод не предполагает использования масштабного производства, поскольку это ручная процедура. Другой известный способ — метод термического разложения подложки карбида кремния[6][7] гораздо ближе к промышленному производству. Поскольку графен впервые[2] был получен только в 2004 году, он ещё недостаточно хорошо изучен и привлекает к себе повышенный интерес.
Данный материал не является просто кусочком других аллотропных модификаций углерода: угля, графита, или алмаза — из-за особенностей энергетического спектра носителей он проявляет специфические[8], в отличие от других двумерных систем, электрофизические свойства.[9]
История открытия[править | править код]
Графен является двумерным кристаллом, состоящим из одиночного слоя атомов углерода, собранных в гексагональную решётку. Его теоретическое исследование началось задолго до получения реальных образцов материала, поскольку из графена можно собрать трёхмерный кристалл графита. Графен является базой для построения теории этого кристалла. Графит является полуметаллом, и как было показано[1] в 1947 году П. Воллесом, в зонной структуре графена также отсутствует запрещённая зона, причём в точках соприкосновения валентной зоны и зоны проводимости энергетический спектр электронов и дырок линеен как функция волнового вектора. Такого рода спектром обладают безмассовые фотоны и ультрарелятивистские частицы, а также нейтрино. Поэтому говорят, что эффективная масса электронов и дырок в графене вблизи точки соприкосновения зон равна нулю. Но здесь стоит заметить, что, несмотря на сходство фотонов и безмассовых носителей, в графене существует несколько существенных различий, делающих носители в графене уникальными по своей физической природе, а именно: электроны и дырки являются фермионами, и они заряжены. В настоящее время, аналогов для этих безмассовых заряженных фермионов среди известных элементарных частиц нет.
Несмотря на такие специфические особенности, экспериментального подтверждения эти выводы не получили до 2005 года[8], вследствие отсутствия материала исследований. Кроме того, ещё раньше было доказано теоретически, что свободную идеальную двумерную плёнку получить невозможно из-за нестабильности относительно сворачивания или скручивания[10]. Тепловые флуктуации приводят к плавлению двумерного кристалла при любой конечной температуре.
Интерес к графену появился снова после открытия углеродных нанотрубок, поскольку вся первоначальная теория строилась на простой модели нанотрубки как развёртки цилиндра. Поэтому теория для графена в приложении к нанотрубкам хорошо проработана.
Попытки получения графена, прикреплённого к другому материалу начались с экспериментов по использованию простого карандаша и продолжились с использованием атомно-силового микроскопа[11] для механического удаления слоёв графита, но не достигли успеха. Использование графита с внедрёнными (интеркалированный графит) в межплоскостное пространство чужеродными атомами (используется для увеличения расстояния между соседними слоями и их расщепления) также не привело к результату.
В 2004 году была опубликована работа в журнале Science[2], где сообщалось о получении графена на подложке окисленного кремния. Таким образом, стабилизация двумерной плёнки достигалась благодаря наличию связи с тонким слоем диэлектрика SiO2 по аналогии с тонкими плёнками выращенными с помощью МПЭ. Впервые были измерены проводимость, эффект Шубникова-де Гааза, эффект Холла для образцов, состоящих из плёнок углерода с атомарной толщиной.
Метод отшелушивания является довольно простым и гибким, поскольку позволяет работать со всеми слоистыми кристаллами, то есть теми материалами, которые представляются как слабо (по сравнению с силами в плоскости) связанные слои двумерных кристаллов. В последующей работе[5] авторы показали, что его можно использовать для получения других двумерных кристаллов: BN, MoS2, NbSe2, Bi2Sr2CaCu2Ox.
Получение[править | править код]

Кусочки графена получают при механическом воздействии на пиролитический графит. Сначала тонкие слои графита помещают между липкими лентами и отщепляют раз за разом тонкие слои графита, пока не будет получен достаточно тонкий слой (среди многих плёнок могут попадаться и однослойные, которые и представляют интерес). После отшелушивания плёнку графена помещают на подложку окисленного кремния. При этом трудно получить плёнку определённого размера и формы в фиксированных частях подложки (горизонтальные размеры плёнок составляют обычно около 10 мкм). Найденные с помощью оптического микроскопа (они слабо видны при толщине диэлектрика 300 нм) плёнки подготавливают для измерений. С помощью атомно-силового микроскопа определяют реальную толщину плёнки графита (она может варьироваться от 0,35 до 0,8 нм для графена). Используя электронную литографию, задают форму плёнки для электрофизических измерений (холловский мост для магнитотранспортных измерений).
Кусочки графена также можно приготовить из графита, используя химические методы[12]. Для начала микрокристаллы графита подвергаются действию смеси серной и соляной кислот. Графит окисляется, и на краях образца появляются карбоксильные группы графена. Их превращают в хлориды при помощи тионилхлорида. Затем, под действием октадециламина в растворах тетрагидрофурана, тетрахлорметана и дихлорэтана, они переходят в графеновые слои толщиной 0,54 нм. Этот химический метод не единственный, и, меняя органические растворители и химикаты, можно получить нанометровые слои графита[13].
В статьях[14][3] описан ещё один химический метод получения графена, встроенного в полимерную матрицу.
Если кристалл пиролитического графита и подложку поместить между электродами, то, как показано работе[15] можно добиться того, что кусочки графита с поверхности, среди которых могут оказаться плёнки атомарной толщина, под действием электрического поля могут перемещаться на подложку окисленного кремния. Для предотвращения пробоя (между электродами прикладывали напряжение от 1 до 13 кВ) между электродами также помещали тонкую пластину слюды.
Существует также несколько сообщений[6][7], посвящённых получению графена, выращенного на подложках карбида кремния SiC(0001) . Графитовая плёнка формируется при термическом разложении поверхности подложки SiC (этот метод получения графена гораздо ближе к промышленному производству), причём качество выращенной плёнки зависит от того, какая стабилизация у кристалла: C-стабилизированная или Si-стабилизированная поверхность — в первом случае качество плёнок выше. В работе[16] та же группа исследователей показала, что, несмотря на то, что толщина слоя графита составляет больше одного монослоя, в проводимости участвует только один слой в непосредственной близости от подложки, поскольку на границе SiC-C из-за разности работ выхода двух материалов образуется нескомпенсированный заряд. Свойства такой плёнки оказались эквивалентны свойствам графена.
На (сайте) указывается дешевый способ получения графена в промышленных масштабах. Он основан на детонации углеродосодержащих органических материалов в замкнутом пространстве. Данный способ производства графена является самым низкозатратным из всех существующих, легкодоступным, экологичным. Он позволяет производить графен не миллиграммами, а целыми граммами. В процессе его производства нет необходимости использовать вредные и токсичные химические вещества.
Дефекты[править | править код]
Идеальный графен состоит исключительно из шестиугольных ячеек. Присутствие пяти- и семиугольных ячеек будет приводить к различного рода дефектам.
Наличие пятиугольных ячеек приводит к сворачиванию атомной плоскости в конус. Если рассмотреть 12 таких дефектов одновременно, то эта структура известна под названием фуллерен. Присутствие семиугольных ячеек приводит к образованию седловидных искривлений атомной плоскости. Комбинация этих дефектов и нормальных ячеек может приводить к образованию различных форм поверхности.
Возможные применения[править | править код]
Считается, что на основе графена можно сконструировать баллистический транзистор. В марте 2006 года группа исследователей из технологического института штата Джорджии заявили, что ими был получен полевой транзистор на графене, а также квантово-интерференционный прибор[17]. Исследователи полагают, что благодаря их достижениям в скором времени появится новый класс графеновой наноэлектроники с базовой толщиной транзисторов до 10 нм. Данный транзистор обладает большим током утечки, то есть нельзя разделить два состояния с закрытым и открытым каналом.
Использовать напрямую графен при создании полевого транзистора без токов утечки не представляется возможным благодаря отсутствию запрещённой зоны в этом материале, поскольку нельзя добиться существенной разности в сопротивлении при любых приложенных напряжениях к затвору, то есть не получается задать два состояния пригодных для двоичной логики: проводящее и непроводящее. Сначала нужно создать, каким-нибудь образом, запрещённую зону достаточной ширины при рабочей температуре (чтобы термически возбуждённые носители давали малый вклад в проводимость). Один из возможных способов предложен в работе[4]. В этой статье предлагается создать тонкие полоски графена, с такой шириной, что благодаря квантово-размерному эффекту ширина запрещённой зоны была достаточной для перехода в диэлектрическое состояние (закрытое состояние) прибора при комнатной температуре (28 мэВ соответстует ширине полоски 20 нм). Благодаря высокой подвижности (имеется в виду, что подвижность выше чем в кремнии, используемом в микроэлектронике) 104 В см−1с−1 быстродействие такого транзистора будет заметно выше. Несмотря на то, что это устройство уже способно работать как транзистор, затвор к нему ещё не создан.
Другая область применения предложена в статье[18] и заключается в использовании графена в качестве очень чуствительного сенсора для обнаружения отдельных молекул химимческих веществ присоединённых к поверхности плёнки. В этой работе исследовались такие вещества как NH3, CO, H20, NO2. Сенсор размером 1 мкм × 1 мкм использовался для детектирования присоединения отдельных молекул NO2 к графену. Принцип действия этого сенсора заключается в том, что разные молекулы могут выступать как доноры и акцепторы, что в свою очередь ведёт к изменению сопротивления графена. В работе[19] теоретически исследуется влияние различных (тех же примесей, использованных в эксперименте) примесей на проводимость графена. В работе[20] было показано, что NO2 молекула является хорошим акцептором из-за своих парамагнитных свойств, а диамагнитная молекула N2O4 создаёт уровень близко к точке электронейтральности. В общем случае примеси, молекулы которых имеют магнитный момент (неспаренный электрон), обладают более сильными легирующими свойствами.
Физика[править | править код]
Физические свойства нового материала можно изучать по аналогии с другими подобными материалами. В настоящее время экспериментальное и теоретическое исследование графена сосредоточено на стандартных свойствах двумерных систем: проводимости, квантовом эффекте Холла, слабой локализации и других эффектах исследованных ранее в двумерном электронном газе.
Теория[править | править код]
В этом параграфе кратко описываются основные положения теории, некоторые из которых получили экспериментальное подтверждение, а некоторые ещё ждут верификации.
Кристаллическая структура[править | править код]
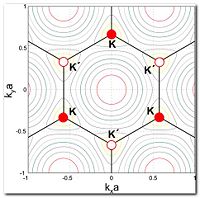
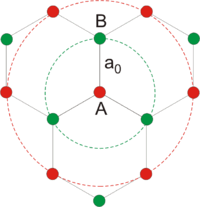
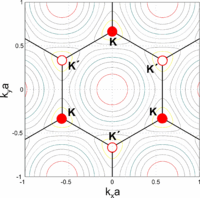
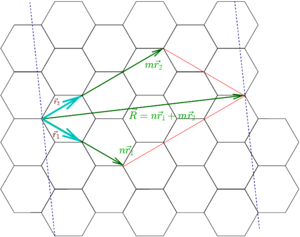
Кристаллическая решётка графена (см. Рис. 3) представляет собой плоскость состоящую из шестиугольных ячеек, то есть является двумерной гексагональной кристаллической решёткой. Для такой решётки известно, что её обратная решётка тоже будет гексагональной. В элементарной ячейке кристалла находятся два атома, обозначенные A и B. Каждый из этих атомов при сдвиге на вектора трансляций (любой вектор вида
Расстояние между ближайшими атомами углерода в шестиугольниках, обозначенное
а соответствующие им вектора обратной решётки:
(без множителя
Зонная структура[править | править код]
Кристаллическая структура материала находит отражение во всех его физических свойствах и, в особенности, зонная структура кристалла сильно зависит от порядка в котором расположены атомы в кристаллической решётке.
Зонная структура графена рассчитана в статье[1] в приближении сильно связанных электронов. На внешней оболочке атома углерода находится 4 электрона, три из которых образуют sp2 гибридизированные связи с соседними атомами в решётки, а оставшийся электрон находится в 2pz состоянии (именно это состояние отвечает за образование межплоскостных связей в графите), а в графене за образование энергетических зон. В приближении сильно связанных электронов полная волновая функция всех электронов кристалла записывается в виде суммы волновых функций электронов из разных подрешёток
В приближении сильно связанных электронов интеграл перекрытия (
Энергетический спектр электронов в графене имеет вид (здесь учтены только ближайшие соседи, координаты которых задаются по формуле (1.3))
Линейный закон дисперсии[править | править код]
Вблизи точек соприкосновения валентной зоны и зоны проводимости из уравнения (2.16) следует, что закон дисперсии для носителей (электронов) в графене представляется в виде:
где
где
Линейный закон дисперсии приводит к линейной зависимости плотности состояний от энергии, в отличии от обычных двумерных систем с параболическим законом дисперсии, где плотность состояний не зависит от энергии. Плотность состояний в графене задаётся стандартным способом
где выражение под интегралом и есть искомая плотность состояний (на единицу площади):
где
Концентрация электронов задаётся интегралом по энергии
где
Здесь также следует обратить внимание на тот факт, что появление линейного закона дисперсии при рассмотрении гексагональной решётки не является уникальной особенностью для данного типа кристаллической структуры, а может появляться и при существенном искажении решётки вплоть до квадратной решётки[21].
Эффективная масса[править | править код]
Благодаря линейному закону дисперсии эффективная масса электронов и дырок в графене равна нулю. Но в магнитном поле возникает другая масса связанная с движением электрона по замкнутым орбитам называемая циклотронной массой. Связь между циклотронной массой и энергетическим спектром для носителей в графене можно получается из следующего рассмотрения. Энергия уровней Ландау для уравнения Дирака задаётся в виде
Из периода осцилляций также можно определить концентрацию носителей
Хиральность и парадокс Клейна[править | править код]
Рассмотрим часть гамильтониана для долины K (см. формулу (3.2)):
Эксперимент[править | править код]
Подавляющее большинство экспериментальных работ посвящено графену, полученному отшелушиванием объёмного кристалла пиролитического графита.
Проводимость[править | править код]
Теоретически показано, что основное ограничение на подвижность электронов и дырок в графене (на Si подложке) возникает из-за заряженных примесей в диэлектрике (SiO2), поэтому сейчас ведутся работы по получению свободновисящих плёнок графена, что должно увеличить подвижность до 1,5×106 см2В−1c−1[27]. Это приведёт к возможности наблюдать дробный квантовый эффект Холла.
Идеальную двумерную плёнку в свободном состоянии нельзя получить из-за её термодинамической нестабильности. Но если в плёнке будут дефекты или она будет деформирована в пространстве (в третьем измерении), то такая «неидеальная» плёнка может существовать без контакта с подложкой[28]. В эксперименте[29] с использованием просвечивающего электронного микроскопа было показано, что свободные плёнки графена существуют и образуют поверхность сложной волнистой формы, с латеральными размерами пространственных неоднородностей около 5—10 нм и высотой — 1 нм. В статье[30] было показано, что можно создать свободную от контакта с подложкой плёнку закреплённую с двух краёв, образуя, таким образом, наноэлектромеханическую систему. В данном случае подвешенный графен можно рассматривать как мембрану, изменение частоты механических колебаний которой предлагается использовать для детектирования массы, силы и заряда, то есть использовать в качестве высокочувствительного сенсора.
Подложка кремния с диэлектриком на котором покоится[2] графен должна быть сильно легирована, для того чтобы её можно было использовать в качестве обратного затвора, при помощи которого можно управлять концентрацией и даже изменять тип проводимости. Поскольку графен является полуметаллом, то приложение положительного напряжения к затвору приводит к электронной проводимости графена и обратно — если приложить отрицательное напряжение, то основными носителями станут дырки, поэтому в принципе нельзя обеднить полностью графен от носителей. Заметим, что если графит состоит из нескольких десятков слоёв, то электрическое поле достаточно хорошо экранированно, как и в металлах, огромным количесвом носителей в полуметалле[11].
В идеальном случае, когда отсутствует легирование и затворное напряжение равно нулю не должно быть носителей тока (см. плотность состояний), что следуя наивным представлениям приводит к отсутствию проводимости, но как показывают эксперименты и теоретические работы[31] вблизи дираковской точки или точки электронейтральности для дираковских фермионов существует конечное значение проводимости, хотя величина минимальной проводимости зависит от метода рассчёта. Эта идеальная область не изучена просто потому, что нет достаточно чистых обрзцов. В действительности все плёнки графена соединены с подложкой и это приводит к неоднородностям, флуктуациям потенциала, что ведёт к пространственной неоднородности типа проводимости по образцу, поэтому даже в точке электронейтральности концентрация носителей теоретически не меньше чем 1012 см−2. Здесь проявляются отличие от обычных систем с двумерным электронным или дырочным газом, а именно отсутствует переход металл-диэлектрик.
Квантовый эффект Холла[править | править код]
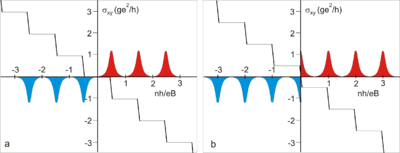
Впервые аномальный (англ. unconventional) квантовый эффект Холла наблюдали в работе[8], где было показано, что носители в графене действительно обладают нулевой эффективной массой, поскольку положения плато на зависимости недиагональной компоненты тензора проводимости соответствовали полуцелым значениям холловской проводимости
Квантовый эффект Холла (КЭХ) может использоваться как эталон сопротивления, потому что численное значение наблюдаемого в графене плато равное
В современных образцах вплоть до 45 Т невозможно наблюдать дробный квантовый эффект Холла, но наблюдается целочисленный квантовый эффект Холла в графене, который не совпадает с обычным квантовым эффектом Холла. В работе[34] наблюдается спиновое расщепление релятивистских уровней Ландау и снятие четырёхкратного вырождения для наинизшего уровня Ландау вблизи точки электронейтральности. Для объяснения этого эффекта предложено несколько теорий[35], но недостаточное количество экспериментального материала не позволяет выбрать среди них правильную.
Любопытные факты[править | править код]
- В статье, опубликованной 10 ноября 2005 года в журнале Nature[8], Константин Новоселов и Андрей Гейм утверждают, что электрические заряды в графене ведут себя как релятивистские частицы с нулевой эффективной массой. Эти частицы, известные как безмассовые фермионы Дирака, и описываются уравнением Дирака, хотя в эффекте Шубникова-де Гааза (осцилляции магнетосопротивления) наблюдаемые осцилляции соответствуют конечной циклотронной массе.
- Так как закон дисперсии для носителей идентичен безмассовым частицам, то графен может выступать в качестве экспериментальной лаборатории для квантовой электродинамики[36].
- Квантовый эффект Холла в графене может наблюдаться даже при комнатной температуре[33] из-за большой циклотронной энергии, при которой температурное размытие функции распеределения Ферми-Дирака меньше этой энергии
- При сворачивании графена в цилиндр (см. Рис. 7) получается одностенная нанотрубка. В зависимости от конкретной схемы сворачивания графитовой плоскости, нанотрубки могут обладать или металлическими или полупроводниковыми свойствами[38].
- В графене отсутствует вигнеровская кристаллизация[39].
- В графене нарушается приближение Борна-Оппенгеймера (адиабатическое приближение), гласящее что в силу медленного движения ионных остовов решётки их можно включить в рассмотрение как возмущение известное как фононы решётки — основное приближение, на котором строится зонная теория твёрдых тел[40].
Примечания[править | править код]
- ↑ Перейти обратно: а б в г д е Wallace P. R. «The Band Theory of Graphite», Phys. Rev. 71, 622 (1947) doi:10.1103/PhysRev.71.622
- ↑ Перейти обратно: а б в г д е Novoselov K. S. et al. «Electric Field Effect in Atomically Thin Carbon Films», Science 306, 666 (2004) doi:10.1126/science.1102896
- ↑ Перейти обратно: а б Stankovich S. et al. «Graphene-based composite materials», Nature 442, 282 (2006) doi:10.1038/nature04969
- ↑ Перейти обратно: а б Chen Z. cond-mat/0701599 [1]
- ↑ Перейти обратно: а б Novoselov, K. S. et al. «Two-dimensional atomic crystals», PNAS 102, 10451 (2005) doi:10.1073/pnas.0502848102
- ↑ Перейти обратно: а б Rollings E. cond-mat/0512226 [2]
- ↑ Перейти обратно: а б Hass J. cond-mat/0604206 [3]
- ↑ Перейти обратно: а б в г д е Novoselov K. S. et al. «Two-dimensional gas of massless Dirac fermions in graphene», Nature 438, 197 (2005) doi:10.1038/nature04233
- ↑ http://news.google.ru/news?hl=ru&newwindow=1&q=%D0%93%D1%80%D0%B0%D1%84%D0%B5%D0%BD&um=1&ie=UTF-8&ei=C_VFSuTwPM6NsAbApZgb&sa=X&oi=news_group&ct=title&resnum=614621089
- ↑ Peierls R., Helv. Phys. Acta 7, 81 (1934); Peierls R., Ann. I. H. Poincare 5, 177 (1935); Landau L. D., Phys. Z. Sowjetvunion 11, 26 (1937); Ландау Л.Д., Лифшиц Е.М. «Курс теоретической физики. Том 5. Статистическая физика». — Физматлит. — 616 стр. с. — ISBN 5922100548..
- ↑ Перейти обратно: а б Zhang Y. et al. Fabrication and electric-field-dependent transport measurements of mesoscopic graphite devices Appl. Phys. Lett. 86, 073104 (2005) doi:10.1063/1.1862334
- ↑ Solution Properties of Graphite and Graphene Sandip Niyogi, Elena Bekyarova, Mikhail E. Itkis, Jared L. McWilliams, Mark A. Hamon, and Robert C. Haddon J. Am. Chem. Soc.; 2006; 128(24) pp 7720 — 7721; (Communication) doi:10.1021/ja060680r
- ↑ Bunch J. S. et al. Coulomb Oscillations and Hall Effect in Quasi-2D Graphite Quantum Dots Nano Lett. 5, 287 (2005) doi:10.1021/nl048111+
- ↑ Stankovich S. et al. «Stable aqueous dispersions of graphitic nanoplatelets via the reduction of exfoliated graphite oxide in the presence of poly(sodium 4-styrenesulfonate)», J. Mater. Chem. 16, 155 (2006) doi:10.1039/b512799h
- ↑ Sidorov A. N. et al.,Electrostatic deposition of graphene Nanotechnology 18, 135301 (2007) doi:10.1088/0957-4484/18/13/135301
- ↑ Berger, C. et al. «Electronic Confinement and Coherence in Patterned Epitaxial Graphene», Science 312, 1191 (2006) doi:10.1126/science.1125925
- ↑ Carbon-Based Electronics: Researchers Develop Foundation for Circuitry and Devices Based on Graphite March 14, 2006 gtresearchnews.gatech.edu Link
- ↑ Schedin F. cond-mat/0610809 [4]
- ↑ Hwang E. H. cond-mat/0610834 [5]
- ↑ Wehling T. O. cond-mat/0703390 [6]
- ↑ Hatsugai Y. cond-mat/0701431 [7]
- ↑ Katsnelson M. I. et al., Chiral tunnelling and the Klein paradox in graphene Nat. Phys. 2, 620 (2006) doi:10.1038/nphys384
- ↑ Cheianov V. V. and Fal’ko V. I., Selective transmission of Dirac electrons and ballistic magnetoresistance of n-p junctions in graphene Phys. Rev. B 74, 041403 (2006) doi:10.1103/PhysRevB.74.041403
- ↑ Trauzettel B. et al., Spin qubits in graphene quantum dots Nat. Phys. 3, 192 (2007) doi:10.1038/nphys544
- ↑ Silvestrov P. G. and Efetov K. B. Quantum Dots in Graphene Phys. Rev. Lett. 98, 016802 (2007) doi:10.1103/PhysRevLett.98.016802
- ↑ Geim A. K., Novoselov K. S. The rise of graphene. Nat. Mat. 6, 183 (2007). doi:10.1038/nmat1849
- ↑ Hwang E. H. cond-mat/0610157 [8]
- ↑ David Nelson (Editor), Steven Weinberg (Editor), T. Piran (Editor). „Statistical Mechanics of Membranes and Surfaces“. — 2nd ed.. — World Scientific, Singapore. — p. 444 с. — ISBN 9789812387608.
- ↑ Meyer J. C. cond-mat/0701379 [9]
- ↑ Bunch J. S. et al., Electromechanical Resonators from Graphene Sheets Science 315, 490 (2007) doi:10.1126/science.1136836
- ↑ Ludwig A. W. W., et al., «Integer quantum Hall transition: An alternative approach and exact results» Phys. Rev. B 50, 7526 (1994) doi:10.1103/PhysRevB.50.7526; Ziegler K., «Scaling behavior and universality near the quantum Hall transition» Phys. Rev. B 55, 10661 (1997) doi:10.1103/PhysRevB.55.10661; Ziegler K., «Delocalization of 2D Dirac Fermions: The Role of a Broken Supersymmetry» Phys. Rev. Lett. 80, 3113 (1998) doi:10.1103/PhysRevLett.80.3113; Katsnelson M. I., «Zitterbewegung, chirality, and minimal conductivity in graphene» Eur. Phys. J. B 51, 157 (2006) doi:10.1140/epjb/e2006-00203-1; Gusynin V. P. et al., «Unconventional Integer Quantum Hall Effect in Graphene» Phys. Rev. Lett. 95, 146801 (2005) doi:10.1103/PhysRevLett.95.146801; Peres N. M. R. et al., «Electronic properties of disordered two-dimensional carbon» Phys. Rev. B 73, 125411 (2006) doi:10.1103/PhysRevB.73.125411; Tworzydlo J. et al., «Sub-Poissonian Shot Noise in Graphene» Phys. Rev. Lett. 96, 246802 (2006) doi:10.1103/PhysRevLett.96.246802; Cserti J. «Minimal longitudinal dc conductivity of perfect bilayer grapheme» Phys. Rev. B 75, 033405 (2007) doi:10.1103/PhysRevB.75.033405; Ziegler K., «Robust Transport Properties in Graphene» Phys. Rev. Lett. 97, 266802 (2006) doi:10.1103/PhysRevLett.97.266802
- ↑ Gusynin V. P. et al. «Unconventional Integer Quantum Hall Effect in Graphene» Phys. Rev. Lett. 95, 146801 (2005) doi:10.1103/PhysRevLett.95.146801
- ↑ Перейти обратно: а б Novoselov K. S. cond-mat/0702408 [10]
- ↑ Zhang Y., et al., «Landau-Level Splitting in Graphene in High Magnetic Fields» Phys. Rev. Lett. 96, 136806 (2006) doi:10.1103/PhysRevLett.96.136806
- ↑ Fuchs J. et al. Spontaneous Parity Breaking of Graphene in the Quantum Hall Regime Phys. Rev. Lett. 98, 016803 (2007) doi:10.1103/PhysRevLett.98.016803; Nomura K. et al., Quantum Hall Ferromagnetism in Graphene Phys. Rev. Lett. 96, 256602 (2006) doi:10.1103/PhysRevLett.96.256602; Abanin D. A. et al., Spin-Filtered Edge States and Quantum Hall Effect in Graphene Phys. Rev. Lett. 96, 176803 (2006) doi:10.1103/PhysRevLett.96.176803; Fertig H. A. et al., Luttinger Liquid at the Edge of Undoped Graphene in a Strong Magnetic Field Phys. Rev. Lett. 97, 116805 (2006) doi:10.1103/PhysRevLett.97.116805; Goerbig M. O. et al., Electron interactions in graphene in a strong magnetic field Phys. Rev. B 74, 161407 (2006) doi:10.1103/PhysRevB.74.161407; Alicea J. et al., Graphene integer quantum Hall effect in the ferromagnetic and paramagnetic regimes Phys. Rev. B 74, 075422 (2006) doi:10.1103/PhysRevB.74.075422; Gusynin V. P. et al., Excitonic gap, phase transition, and quantum Hall effect in graphene Phys. Rev. B 74, 195429 (2006) doi:10.1103/PhysRevB.74.195429
- ↑ A. Castro Neto et al. Drawing conclusions from graphene Phys. World 19 (11), p 33 (2006) ISSN 0953-8585.
- ↑ Sharapov S. G. et al. «Magnetic oscillations in planar systems with the Dirac-like spectrum of quasiparticle excitations» Phys. Rev. B 69, 075104 (2004) doi:10.1103/PhysRevB.69.075104.
- ↑ R. Saito, G. Dresselhaus, M. S. Dresselhaus. „Physical Properties of Carbon Nanotubes“. — World Scientific. — p. 272 с. — ISBN 1860942237.
- ↑ Dahal H. P. et al. «Absence of Wigner crystallization in graphene» Phys. Rev. B 74, 233405 (2006) doi:10.1103/PhysRevB.74.233405
- ↑ Pisana S. et al. cond-mat/0611714 [11]
См. также[править | править код]
Ссылки[править | править код]
- Mesoscopic physics group — сайт исследовательской группы из университета Манчестера. (англ.)
- Kim group — сайт лаборатории профессора Кима из Колумбийского университета. (англ.)
- Галерея фотографий графита и графена (англ.)
- [12]
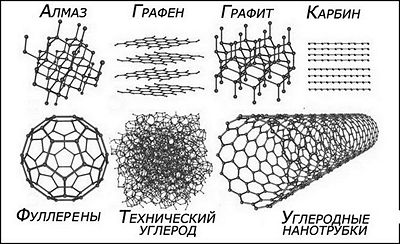
| Аллотропные формы углерода |
| Алмаз | Графен | Графит | Карбин | Технический углерод | Углеродные нанотрубки | Фуллерены |