Телесный угол
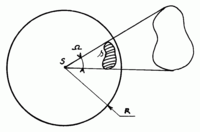
Теле́сный у́гол — часть пространства, которая является объединением всех лучей, выходящих из данной точки (вершины угла) и пересекающих некоторую поверхность (которая называется поверхностью, стягивающей данный телесный угол). Частными случаями телесного угла являются трёхгранные и многогранные углы. Границей телесного угла является некоторая коническая поверхность.
Телесный угол измеряется отношением площади той части сферы с центром в вершине угла, которая вырезается этим телесным углом, к квадрату радиуса сферы: $$\Omega\,=\,{S\over R^2}.$$
Очевидно, телесные углы измеряются отвлечёнными (безразмерными) числами. Единицей измерения телесного угла в системе СИ (система единиц) является стерадиан, равный телесному углу, вырезающему из сферы единичного радиуса поверхность с площадью в 1 квадратную единицу. Полная сфера образует телесный угол, равный 4π стерадиан (полный телесный угол), для вершины, расположенной внутри сферы, в частности, для центра сферы; таким же является телесный угол, под которым видна любая замкнутая поверхность из точки, полностью охватываемой этой поверхностью, но не принадлежащей ей. Кроме стерадианов, телесный угол может измеряться в квадратных градусах, квадратных минутах и квадратных секундах, а также в долях полного телесного угла.
Телесный угол имеет нулевую физическую размерность.
Двойственный телесный угол к данному телесному углу Ω определяется как угол, состоящий из лучей, образующих с любым лучом угла Ω неострый угол.
Коэффициенты пересчёта единиц телесного угла.
| Стерадиан | Кв. градус | Кв. минута | Кв. секунда | Полный угол | |
|---|---|---|---|---|---|
| 1 стерадиан = | 1 | (180/π)² ≈ ≈ 3282,806 кв. градусов |
(180×60/π)² ≈ ≈ 1,1818103×107 кв. минут |
(180×60×60/π)² ≈ ≈ 4,254517×1010 кв. секунд |
1/4π ≈ ≈ 0,07957747 полного угла |
| 1 кв. градус = | (π/180)² ≈ ≈ 3,0461742×10−4 стерадиан |
1 | 60² = = 3600 кв. минут |
(60×60)² = = 12 960 000 кв. секунд |
π/(2×180)² ≈ ≈ 2,424068×10−5 полного угла |
| 1 кв. минута = | (π/(180×60))² ≈ ≈ 8,461595×10−8 стерадиан |
1/60² ≈ ≈ 2,7777778×10−4 кв. градусов |
1 | 60² = = 3600 кв. секунд |
π/(2×180×60)² ≈ ≈ 6,73352335×10−9 полного угла |
| 1 кв. секунда = | (π/(180×60×60))² ≈ ≈ 2,35044305×10−11 стерадиан |
1/(60×60)² ≈ ≈ 7,71604938×10−8 кв. градусов |
1/60² ≈ ≈ 2,7777778×10−4 кв. минут |
1 | π/(2×180×60×60)² ≈ ≈ 1,87042315×10−12 полного угла |
| Полный угол = | 4π ≈ ≈ 12,5663706 стерадиан |
(2×180)²/π ≈ ≈ 41252,96125 кв. градусов |
(2×180×60)²/π ≈ ≈ 1,48511066×108 кв. минут |
(2×180×60×60)²/π ≈ ≈ 5,34638378×1011 кв. секунд |
1 |
Телесный угол обычно обозначается буквой Ω.
Содержание
Вычисление телесных углов[править]
Для произвольной стягивающей поверхности \(S\) телесный угол \(\Omega\), под которым она видна из начала координат, равен
\(\Omega = \iint\limits_S d\Omega = \iint\limits_S{ \href {//traditio.wiki/%D0%A1%D0%B8%D0%BD%D1%83%D1%81}{ \texttip { \sin}{ Синус }}} \vartheta d\varphi d\vartheta = \iint\limits_S \frac{(\mathbf{r}/r)\cdot \mathbf{n}dS}{r^2},\)
где \(r, \vartheta, \varphi\) — сферические координаты элемента поверхности \(dS,\) \(\mathbf{r}\) — его радиус-вектор, \(\mathbf{n}\) — единичный вектор, нормальный к \(dS.\)
Свойства телесных углов[править]
- Полный телесный угол (полная сфера) равен \(4\pi\) стерадиан.
- Сумма всех телесных углов, двойственных к внутренним телесным углам выпуклого многогранника, равна полному углу.
Величины некоторых телесных углов[править]
- Треугольник с координатами вершин \(\mathbf{r}_1\), \(\mathbf{r}_2\), \(\mathbf{r}_3\) виден из начала координат под телесным углом
\(\Omega = 2\, \mathrm{arctg}\, \frac{(\mathbf{r}_1\mathbf{r}_2\mathbf{r}_3)}{r_1r_2r_3 + (\mathbf{r}_1\cdot\mathbf{r}_2)r_3 + (\mathbf{r}_2\cdot\mathbf{r}_3)r_1 + (\mathbf{r}_3\cdot\mathbf{r}_1)r_2},\)
где \((\mathbf{r}_1\mathbf{r}_2\mathbf{r}_3)\) — смешанное произведение данных векторов, \((\mathbf{r}_i\cdot\mathbf{r}_j)\) — скалярные произведения соответствующих векторов, полужирным шрифтом обозначены векторы, нормальным шрифтом — их длины. Используя эту формулу, можно вычислять телесные углы, стянутые произвольными многоугольниками с известными координатами вершин (для этого достаточно разбить многоугольник на непересекающиеся треугольники).
- Телесный угол при вершине прямого кругового конуса с углом раствора α равен \(\Omega = 2\pi (1 -{ \href {//traditio.wiki/%D0%9A%D0%BE%D1%81%D0%B8%D0%BD%D1%83%D1%81}{ \texttip { \cos}{ Косинус }}} \frac{\alpha}{2})\). Если известны радиус основания \(R\) и высота \(H\) конуса, то \(\Omega = 2\pi (1 - \frac{H}{\sqrt{R^2+H^2}})\). Когда угол раствора конуса мал, \(\Omega \approx \frac{\pi \alpha^2}{4}\) (\(\alpha\) выражено в радианах), или \(\Omega \approx 0,000239 \alpha^2\) (\(\alpha\) выражено в градусах). Так, телесный угол, под которым с Земли видны Луна и Солнце (их угловой диаметр примерно равен 0,5°), составляет около 6×10−5 стерадиан, или ≈0,0005 % площади небесной сферы (то есть полного телесного угла).
- Телесный угол при вершине куба (или любого другого прямоугольного параллелепипеда) равен \(\frac{1}{8}\) полного телесного угла, или \(\frac{\pi}{2}\) стерадиан.
См. также[править]
ast:Ángulu sólidu eo:Solida angulo hu:Térszög lv:Telpas leņķis
![Счётчик WikiStats](/counter.png?request=GET%20/%25D0%25A2%25D0%25B5%25D0%25BB%25D0%25B5%25D1%2581%25D0%25BD%25D1%258B%25D0%25B9_%25D1%2583%25D0%25B3%25D0%25BE%25D0%25BB%20HTTP/1.1&status=200&body_bytes_sent=0&http_referer=&arg_title=%25D0%25A2%25D0%25B5%25D0%25BB%25D0%25B5%25D1%2581%25D0%25BD%25D1%258B%25D0%25B9_%25D1%2583%25D0%25B3%25D0%25BE%25D0%25BB&wiki_action=view&upstream_cache_status=MISS"){kind=small}