Поляризация электромагнитных волн
Поляризация электромагнитных волн (в частности, света) — одно из фундаментальных свойств электромагнитного излучения, состоящее в неравноправии различных направлений в плоскости, перпендикулярной световому лучу (поперечно направлению распространения световой волны) — явление направленного колебания векторов напряженности электрического поля E или напряженности магнитного поля H.
Поперечность световых волн (как и любых др. электромагнитных волн) выражается в том, что колеблющиеся в них векторы напряжённости электрического поля Е и напряжённости магнитного поля Н перпендикулярны к направлению распространения волны. Е и Н выделяют (отсюда указанное выше неравноправие) определённые направления в пространстве, занятом волной. Кроме того, Е и Н почти всегда взаимно перпендикулярны, поэтому для полного описания состояния поляризации света требуется знать поведение лишь одного из них. Обычно для этой цели выбирают вектор Е.
Поляризацией света называют также геометрические характеристики, которые отражают особенности этого поведения.[1]
Когерентное электромагнитное излучение может иметь:
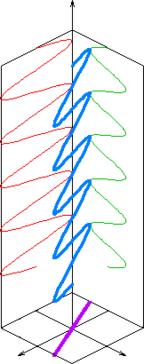
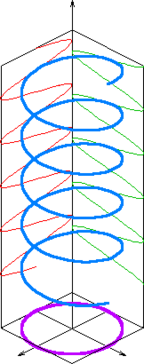
- Линейную поляризацию — в направлении, перпендикулярном направлению распространения волны;
- Круговую поляризацию — правую либо левую, в зависимости от направления вращения вектора индукции;
- Эллиптическую поляризацию — случай, промежуточный между круговой и линейными поляризациями.
Некогерентное излучение может не быть поляризованным, либо быть полностью или частично поляризованным любым из указанных способов. В этом случае понятие поляризации понимается статистически.
При теоретическом рассмотрении поляризации волна полагается распространяющейся горизонтально. Тогда можно говорить о вертикальной и горизонтальной линейных поляризациях волны.
Теория явления[править | править код]
Электромагнитная волна может быть разложена (как теоретически, так и практически) на две поляризованные составляющие, например поляризованные вертикально и горизонтально. Возможны другие разложения, например по иной паре взаимно перпендикулярных направлений, или же на две составляющие, имеющие левую и правую круговую поляризацию. При попытке разложить линейно поляризованную волну по круговым поляризациям (или наоборот) возникнут две составляющие половинной интенсивности.
Как с квантовой, так и с классической точки зрения, поляризация может быть описана двумерным комплексным вектором (вектором Джонса). Поляризация фотона является одной из реализаций q-бита.
Свет солнца, являющийся тепловым излучением, не имеет поляризации, однако рассеянный свет неба приобретает частичную линейную поляризацию. Поляризация света меняется также при отражении. На этих фактах основаны применения поляризующих фильтров в фотографии и т. д.
Линейную поляризацию имеет обычно излучение антенн.
По изменению поляризации света при отражении от поверхности можно судить о структуре поверхности, оптических постоянных, толщине образца.
Если рассеянный свет поляризовать, то, используя поляризационный фильтр с иной поляризацией, можно ограничивать прохождение света. Интенсивность света прошедшего через поляризаторы подчиняется закону Малюса. На этом принципе работают жидкокристаллические экраны.
Некоторые насекомые, например пчёлы, способны различать линейную поляризацию света, что даёт им дополнительные возможности для ориентации в пространстве. Обнаружено, что и некоторые животные, например, креветка-богомол павлиновая[2] способны различать циркулярно-поляризованный свет, и свет оказывается с круговой поляризацией. В определённых условиях глаз человека также может отличать поляризованный свет от неполяризованного.
История[править | править код]
В 1669 г. датский учёный Эразм Бартолин сообщил о своих опытах с кристаллами известкового шпата (CaCO3), чаще всего имеющими форму правильного ромбоэдра, которые привозили возвращающиеся из Исландии моряки. Он обнаружил, что луч света при прохождении сквозь кристалл расщепляется на два луча (называемых теперь обыкновенным и необыкновенным). Бартолин провёл тщательные исследования обнаруженного им явления двойного лучепреломления, однако объяснения ему дать не смог.
Спустя двадцать лет после опытов Э. Бартолина, его открытие привлекло внимание нидерландского учёного Христиана Гюйгенса, который начал исследовать свойства кристаллов исландского шпата и дал объяснение явлению двойного лучепреломления на основе своей волновой теории света. При этом он ввёл важное понятие оптической оси кристалла, при вращении вокруг которой отсутствует анизотропия свойств кристалла, то есть их зависимость от направления (такой осью обладают не все кристаллы).
В своих опытах Гюйгенс в развитие открыий Бартолина, он пропускал оба луча, вышедшие из кристалла исландского шпата, сквозь второй такой же кристалл. Оказалось, что если оптические оси обоих кристаллов параллельны, то дальнейшего разложения этих лучей уже не происходит. Если же второй ромбоэдр повернуть на 180 градусов вокруг направления распространения обыкновенного луча, то при прохождении через второй кристалл необыкновенный луч претерпевает сдвиг в направлении, противоположном сдвигу в первом кристалле, и из такой системы оба луча выйдут соединёнными в один пучок. Выяснилось также, что в зависимости от величины угла между оптическими осями кристаллов изменяется интенсивность обыкновенного и необыкновенного лучей.
Эти исследования вплотную подвели Гюйгенса к открытию явления поляризации света, однако решающего шага он сделать не смог, поскольку световые волны в его теории предполагались продольными. Для объяснения опытов Х. Гюйгенса И. Ньютон, придерживавшийся корпускулярной теории света, выдвинул идею об отсутствии осевой симметрии светового луча и этим сделал важный шаг к пониманию поляризации света.
В 1808 г. французский физик Этьен Луи Малюс, глядя сквозь кусок исландского шпата на блестевшие в лучах заходящего солнца окна Люксембургского дворца в Париже, к своему удивлению заметил, что при определённом положении кристалла было видно только одно изображение. На основании этого и других опытов и опираясь на корпускулярную теорию света Ньютона, он предположил, что корпускулы в солнечном свете ориентированы беспорядочно, но после отражения от какой-либо поверхности или прохождения сквозь анизотропный кристалл они приобретают определённую ориентацию. Такой «упорядоченный» свет он назвал поляризованным.
Параметры Стокса[править | править код]
В общем случае плоская монохроматическая волна имеет правую или левую эллиптическую поляризацию. Полная характеристика эллипса даётся тремя параметрами, например, полудлинами сторон прямоугольника, в который вписан эллипс поляризации , и разностью фаз , либо полуосями эллипса , и углом между осью и большой осью эллипса. Удобно описывать эллиптически поляризованную волну на основе параметров Стокса: , .
Независимыми являются только три из них, ибо справедливо тождество:
Если ввести вспомогательный угол , определяемый выражением (знак соответствует правой, а — левой поляризации), то можно получить следующие выражения для параметров Стокса:
На основе этих формул можно характеризовать поляризацию световой волны наглядным геометрическим способом. При этом параметры Стокса , , интерпретируются, как декартовы координаты точки, лежащей на поверхности сферы радиуса . Углы и имеют смысл сферических угловых координат этой точки. Такое геометрическое представление предложил Пуанкаре, поэтому эта сфера называется сферой Пуанкаре.
Наряду с , , используют также нормированные параметры Стокса , , . Для поляризованного света .
См. также[править | править код]
Литература[править | править код]
- Ахманов С. А., Никитин С. Ю. — Физическая оптика, 2 издание, M. — 2004.
- Борн М., Вольф Э. — Основы оптики, 2 издание, исправленное, пер. с англ.,М. — 1973