LAB
Цветовое пространство Lab — аббревиатура названия двух разных (хотя и похожих) цветовых пространств.
Более известным является CIELAB (точнее, CIE 1976 L*a*b*), это пространство принято в качестве международного стандарта. Более ранняя версия 1966 г., Hunter Lab (точнее, Hunter L, a, b) в настоящее время имеет лишь исторический интерес.
- Под пространством Lab чаще всего подразумевают CIELAB, хотя неформальная аббревиатура Lab и не определяет цветовое пространство однозначно.
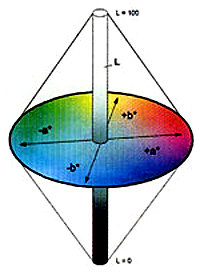
При разработке Lab преследовалась цель создания цветового пространства, где изменения цвета выражается более линейным с точки зрения человеческого восприятия (по сравнению с XYZ), чтобы одинаковое изменение значений координат цвета (градиент приращений) в разных областях цветового пространства производило пропорциональное ощущение изменения цвета. Математически же, чтобы корректировалась нелинейность восприятия цвета человеком. Оба цветовых пространства рассчитываются относительно определенного значения точки белого (см. Рис.1) на оси L, проходящей через точки белого). Если значение точки белого дополнительно не указывается, подразумевается, что значения Lab рассчитаны для стандартного осветителя D50.
История создания модели цветового пространства Lab[править | править код]
В 1931 году после серии экспериментов по оценке восприятия цвета человеком Международная комиссия по освещению разработала стандарт CIE 1931 XYZ. Это цветовое пространство вмещало в себя все воспринимаемые человеком цвета. Чтобы устранить нелинейность XYZ в 1960 году Мак-Адам предложил пространство UVW. В 1964 году Вишецким была предложена модель U*V*W. В 1966 году была предложена модель Хантера (Hunter L, a, b), а в 1976 году, после устранения разногласий была разработана модель CIE L*a*b*, которая является сейчас международным стандартом. [1]
Все эти цветовые пространства стремились уменьшить нелинейность изменения цвета в разных частях области цветового охвата, однако, идеального в этом отношении стандарта так и не появилось. В Hunter Lab наблюдается сжатие в желтой части и расширение в синей. В CIELAB, хотя она разработана на основе Hunter Lab и должна была устранить имеющиеся недостатки, отмечается расширение в желтой части. Оба цветовых пространства вычисляются из пространства CIE 1931 XYZ, однако преобразования в CIELAB осуществляются с использованием кубических корней, в то время как в Hunter Lab использованы квадратные. [2]
Формулы определения координат CIELAB[править | править код]
Преобразование XYZ -> L*a*b*
где
Значения
Разделение функции
(соответствует значению) (соответствует кривой)
Значение
где
- Обратное преобразование L*a*b* -> XYZ
Формулы обратного преобразования (при
- задать
- задать
- задать
- если
- если
- если
Практический смысл значений Lab[править | править код]
В цветовом пространстве Lab значение светлоты отделено от значения хроматической составляющей цвета (тон, насыщенность). Светлота задана координатой L (изменяется от 0 до 100, то есть от самого темного до самого светлого), хроматическая составляющая — двумя декартовыми координатами a и b. Первая обозначает положение цвета в диапазоне от зеленого до пурпурного, вторая — от синего до желтого.
Использование Lab[править | править код]
В отличие от цветовых пространств RGB или CMYK, которые являются, по сути, набором аппаратных данных для воспроизведения цвета на бумаге или на экране монитора (цвет может зависеть от типа печатной машины, марки красок, влажности воздуха в цеху или производителя монитора и его настроек), математическая модель Lab однозначно определяет цвет. Поэтому Lab нашел широкое применение в программном обеспечении для обработки изображений в качестве промежуточного цветового пространства, через которое происходит конвертирование данных между другими цветовыми пространствами (например, из RGB сканера в CMYK печатного процесса). При этом особые свойства Lab сделали редактирование в этом пространстве мощным инструментом цветокоррекции.
Благодаря характеру определения цвета в Lab появляется возможность отдельно воздействовать на яркость, контраст изображения и на его цвет. Во многих случаях это позволяет ускорить обработку изображений, например, при допечатной подготовке. Lab предоставляет возможность избирательного воздействия на отдельные цвета в изображении, усиления цветового контраста, незаменимыми являются и возможности, которые это цветовое пространство предоставляет для борьбы с шумом на цифровых фотографиях [3] [4].
Недостатки и критика LAB[править | править код]
Ввиду того что для преобразования из XYZ в LAB используются формулы, содержащие кубические корни, LAB представляет из себя сильно-нелинейную систему. Это затрудняет применение привычных операций над 3-х мерными векторами в этом цветовом пространстве. Две наиболее широко используемые формулы цветового различия[5], используемые в программах обработки изображений — CIEDE1976, вычисляемая как расстояние между точками в евклидовом пространстве (квадратный корень из суммы квадратов разностей координат), и CIEDE2000, более поздний стандарт, дающая гораздо лучший результат, но в то же время чрезвычайно сложная для вычислений.[6][7]
LAB при разработке оптимизировался для применения в условиях известного (как правило, студийного) освещения, и из-за этого LAB трудно применим для сцен в которых присутствуют несколько источников света, ни один из которых не может считаться основным.
LAB также неприменим для редактирования фотографий с высоким динамическим диапазоном яркости — ни одна из известных программ для обработки HDR изображений не поддерживает LAB (см. HDR (англ.)).
Cм. также[править | править код]
Ссылки[править | править код]
- ↑ Цвет для жизни — Компьютера
- ↑ Hunter L,a, b Versus CIE 1976 L*a*b* (PDF)
- ↑ Дэн Маргулис Photoshop для профессионалов. Классическое руководство по цветокоррекции — М:. Интерсофтмарк, 2003. ISBN 5-902569-04-4
- ↑ Дэн Маргулис Photoshop LAB Color. Загадка каньона и другие приключения в самом мощном цветовом пространстве — М:. Интелбук, 2006. ISBN 5-91157-002-5 0-321-35678-0
- ↑ "Evaluation of the the CIE Color Difference Formulas" (англ.).
- ↑ "The CIEDE2000 Color-Difference Formula: Implementation Notes, Supplementary Test Data, and Mathematical Observations" (PDF) (англ.).
- ↑ Формула CIE DE1994 практически не используется, так как была заменена CIE DE2000
| Цветовые модели | ||
|---|---|---|
| Наименование: | ▸ RGB (цветовая модель) • XYZ • HSV • HSL и HSV • RYB • LAB • PMS (Пантон) • Манселла • NCS • RAL • YUV • YCbCr • YPbPr • YDbDr • YIQ • |  |
| ∘ ∘ ∘ | ||