Участник:Миг/Математика цветного зрения

Математика цветного зрения — комплекс представлений для математического описания «физического цвета», как комбинации чистых спектральных цветов из видимого диапазона электромагнитного излучения. Существует бесконечное множество различных спектральных цветов, большинство из которых не имеют названий (см. Имя цвета).
Набор всех физических цветов можно интерпретировать как векторы в бесконечномерном векторном пространстве, более узко - в гильбертовом пространстве (en:Hilbert_space). Его называют цветовым пространством, Hcolor.
Место физических цветов можно интерпретировать как симплексы в (математическом) конусе, вершины которого — спектральные цвета. Белый цвет (свет) располагается на оси (в точке пересечения оси и основания конуса) (en:Centroid) симплекса, черно-белый — только на оси конуса (внизу - чёрный, вверху - белый, между ними — оттенки серого), и монохроматические цвета, связанные с осью с любой данной вершиной где-нибудь по линии оси от этих вершин в любых плоскостях сечений конусов в зависимости от их яркости. (Максимально яркие цвета спектра располагаются в плоскости наибольшего диаметра сечений конусов, в середине оси)(см. рис.3).
Элемент C Hcolor является функцией из диапазона видимых осознаваемых ощущений от длин волны, в интервале реальных чисел [Wmin,Wmax], с соответствием каждой длине волны w [Wmin,Wmax] - интенсивность C(w).
У людей воспринимаемый цвет может быть смоделирован как три числа: степень стимуляции каждого из 3-х типов колбочек (т.е. клетками, состоящими из трёх колбочек с зонами условного восприятия диапазона основных цветов RGB). Таким образом о человеческом восприятии цвета можно думать как о векторе в 3-мерном Евклидовом пространстве. Мы называем этот вектор R3цвет.[1]
- Евклидовое пространство.
С современной точки зрения, существует, по сути, только одно евклидово пространство каждого измерения. В декартовых координатах моделируются реальные координатные пространства (Rn) той же размерности. В измерении, это является реальной линией; в двойной размерности — это Декартовые плоскости; в более высоких измерениях — это координатное пространство с тремя или более реальным числом координат. Математики обозначают n-мерном Евклидово пространство как En, если они хотят подчеркнуть свою евклидову природу, но Rn используется также, поскольку Rn считается стандартной Евклидовой структурой. (Но эти две структуры не всегда отличали Евклидовые пространства конечных измерений).[2]
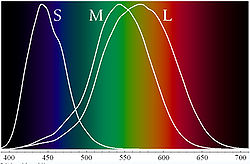
Начиная с каждой длины волны — w стимулирует каждый из 3 типов клеток колбочек сетчатки глаза до известной степени, и эти степени могут быть представлены 3 функциями клеток-колбочек s (w), м. (w), l (w) ответу S, М., L, соответственно. (см. рис.3).
Наконец, так как пучок света может быть составным, состоящим из излучений многих различных длин волны, определять степень, в которой физический цвет C в Hцвет стимулирует каждую клетку конуса, мы должны вычислить интеграл (относительно w), по интервалу [Wmin,Wmax], из C (w) *s (w), C (w) *m (w), и C (w) *l (w) (см. рис.3). Тройные из получающихся чисел связываются к каждому «физическому» цвету C (который является областью в Hцвет) к специфическому воспринятому цвету (который является единственным пунктом в R3цвет). Эта функция, как легко можно заметить, является линейной. Может также быть легко замечено, что много различных областей в «физическом» месте Hцвет может все привести к тому же самому единственному воспринятому цвету в R3цвет. Таким образом, воспринятый цвет не уникален для одного физического цвета.
Таким образом человеческое цветное восприятие определено определенной, групповой линейной картографией от бесконечномерного места Hilbert Hцвет к 3-мерному Евклидовому месту en:Euclidean_spaceR3цвет.
Технически, изображение (математического) конуса по симплексу, вершины которого - спектральные цвета, этой линейной картографией, является также (математическим) конусом в R3цвет. Перемещение непосредственно далеко от вершины этого конуса представляет поддержание той же самой цветности, увеличивая ее интенсивность. Взятие поперечного сечения этого конуса приводит к 2-ому месту цветности. И трехмерный конус и его проектирование или поперечное сечение - выпуклые наборы; то есть, любая смесь спектральных цветов - также цвет.
Международная комиссия по освещению 1931 ХУ (см. рис.2) — диаграмма цветности в плоскости. Местоположение Planckian показывают величины с цветными температурами, помеченными в градусах Келвина. Внешняя кривая — граница - спектральное (или монохроматическое) местоположение, с длинами волны, показанными в (синих) миллимикронах. Отметьте, что цвета в этом файле (изображении) определяются, используя sRGB. Области вне треугольника не могут быть точно предоставлены, потому что они - вне гаммы sRGB, поэтому они интерпретировались. Отметьте, что изображенные цвета зависят от цветного места устройства, на котором рассматривается изображение, и поэтому не можете быть строго точного представления цвета в специфическом положении. Практически, было бы весьма трудно измерить три ответа колбочек человека на различные физические цветные стимулы. Так, взамен используются три основных определенных цветов RGB оценочных испытаний. Именно — S, М, и L (см.рис.3). Чтобы калибровать человеческое перцепционное место, ученые позволили для человеческих испытаний пробовать объекты (предметы), соответствующие любому физическому цвету, поворачивая диски, чтобы создать определенные комбинации интенсивности intensities (яS, ЯМ, ЯL) для S, М, и огней L, resp., пока не было найден результат. Это должно было только быть сделано для физических цветов, которые являются спектральными (так как линейная комбинация спектральных цветов будет подобрана той же самой линейной комбинацией их (яS, ЯМ, ЯL —«спички»). Отметьте, что практически, часто по крайней мере один из S, М, L должен был бы быть добавлен с небольшим количеством интенсивности к физическому испытательному цвету, и той комбинации, подобранной линейной комбинацией сохранения 2 цветов. Среди различных людей (без дальтонизма), соответствия оказались почти идентичными.
Рассматривая все получающиеся комбинации intensities (яS, ЯМ, ЯL) как подмножество 3 мест сформирована модель для человеческого перцепционного цветного места. (Отметьте, что, когда один из S,М, L должен был быть добавлен к испытательному цвету, его интенсивность была подсчитана как отрицательная.) Снова, это, оказывается, (математический) конус, а не квадрика, и скорее все лучи через создание в 3 местах, проходящих через определенный выпуклый набор. Снова, этот конус имеет свою форму, когда перемещаясь непосредственно далеко от происхождения, соответствует увеличению интенсивности S, М, L огни пропорционально. И снова поперечное сечение этого конуса — плоская форма, которая является (по определению) местом «цветностей» (неофициально: отличные цвета). Одна деталь — такое поперечное сечение, соответствуя постоянному X+Y+Z Международной комиссии по освещению, 1931, красит место, дает диаграмму цветности Международной комиссии по освещению.
Должно быть отмечено, что эта система подразумевает, что для любого оттенка или неспектрального цвета есть бесконечно много отличающихся физических спектров, которые все восприняты как тот оттенок или цвет, получаемый при исключении цвета на линии пурпурных цветов en:Line_of_purples. Вообще нет такой вещи как комбинация спектральных цветов, что мы чувствуем, как (говорят) загар; вместо этого есть бесконечно много возможностей, которые производят тот точный цвет.
Единственные исключения к этому правилу - перцепционные цвета, соответствующие границе конуса. Другими словами, те цветности на простой закрытой кривой, которая является границей 1931 диаграммы C.I.E., изображенной в фигуре. Они включают точно все спектральные цвета плюс «линия пурпурных цветов» соединения концов спектральных цветов: для каждого из них, в H есть только один физический цвет, цвет этот может создать тот воспринятый цвет.
Диаграмма цветности Международной комиссии по освещению имеет форму подковы, с ее кривым краем, соответствующим всем спектральным цветам (спектральное местоположение) en:Locus_(mathematics), и остающийся прямой край, соответствующий наиболее важным пурпурным оттенкам, отображаемых обычно как смеси красных и фиолетовых цветов.
Преобразование Фон Криса[править | править код]
Цветной метод адаптации фон Криса — техника, которая иногда используется при закрытых дверях обработки изображения. Метод должен применить подход к каждой человеческой ячейке колбочки, которая при спектральных ответах чувствительности должна обеспечить приспособленное к появлению ссылки, обеспечивающей постоянство появления белого цвета. К заявлению Иоганнеса фон Криса en:Johannes_von_Kries относительно адаптивной прибыли на трех типах фоторецепторов колбочек en:Cone_cell сначала обращались к методу цветного постоянства Герберт Э. Ивес en:Herbert_E._Ives [3],[4] и метод иногда упоминается как Ives, преобразовывающий[5] или von Kries–Ives адаптация.[6]
Коэффициент von Криса en:Von_Kries управляет отдыхом при условии, что цветное постоянство en:Color_constancy достигнуто, индивидуально приспосабливая прибыль трех ответов ячейки колбочки, прибыль в зависимости от сенсорного контекста, то есть, цветной истории и окружать. Таким образом, ответы колбочки c' от двух излучающих спектров могут быть подобраны соответствующим выбором диагональной адаптации matrices и [7]: где S - матрица чувствительности конуса, и f - спектр стимула создания условий. Это приводит к методу von Криса, который преобразовывают для цветной адаптации место цвета en:LMS_color_space LMS (ответы длинной-, средней-, и место ответа ячейки короткой длины волны):
Эта диагональная матрица D наносит на карту ответы конуса, или цвета, в одном государстве адаптации к передаче цветов в другом; когда государство адаптации, как предполагают, определено источником света, эта матрица полезна, поскольку освещающая адаптация преобразовывает. Элементы диагональной матрицы D - отношения ответов колбочки (на длинные, средние, короткие волны) для «белого» источника света en:White_point.
Более полные von Kries преобразования, для цветов, представленных в XYZ en:CIE_1931_color_space или цветном месте RGB, включает матричные преобразования в и из места LMS место en:LMS_Color_Space с диагональю преобразовывают D в середине.[8]
См. также[править | править код]
Ссылки[править | править код]
- ↑ http://en.wikipedia.org/wiki/Color_vision
- ↑ http://en.wikipedia.org/wiki/Euclidean_space
- ↑ Ives HE (1912). "The relation between the color of the illuminant and the color of the illuminated object". Trans. Illuminat. Eng. Soc. 7: 62–72. (Reprinted in: Brill, Michael H. (1995). "The relation between the color of the illuminant and the color of the illuminated object". Color Res. Appl. 20: 70–5. doi:10.1002/col.5080200112. )
- ↑ Hannah E. Smithson and Qasim Zaidi (2004). "Colour constancy in context: Roles for local adaptation and levels of reference". Journal of Vision 4 (9): 693–710. doi:10.1167/4.9.3. PMID 15493964. http://www.journalofvision.org/4/9/3/article.aspx.
- ↑ Hannah E. Smithson (2005). "Review. Sensory, computational and cognitive components of human colour constancy". Philosophical Transactions of the Royal Society 360 (1458): 1329–46. doi:10.1098/rstb.2005.1633. http://journals.royalsociety.org/content/px26ma7w586vq2a7/.
- ↑ Karl R. Gegenfurtner, L. T. Sharpe (1999). Color Vision: From Genes to Perception. Cambridge University Press. ISBN 052100439X. http://books.google.com/books?id=9R1ogJsPHi8C&pg=PA413&dq=von-kries+ives&ei=gYuSR--JOZ6ktgOAkPVE&ie=ISO-8859-1&sig=9fSl-f7sE95QZ2mfBQSauPMhvrc.
- ↑ Gaurav Sharma (2003). Digital Color Imaging Handbook. CRC Press.
- ↑ Erik Reinhard (2006). High Dynamic Range Imaging: Acquisition, Display, and Image-Based Lighting. Morgan Kaufmann. ISBN 0125852630. http://books.google.com/books?id=dH2lRxTg1UsC&pg=PA39&dq=von-kries-transform&ei=fIGSR6jlBoiGsgOK4qE9&sig=OjjbcXI1dbMkdqZWm3ojUvqV92Q#PPA36,M1.
- перенаправление шаблон:цвета радуги
| Web colors | black | silver | grey | white | red | maroon | purple | fuchsia | green | lime | olive | yellow | orange | blue | navy | teal | aqua |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|