Симплекс
Симплекс — (от лат. simplex — простой) (математический), простейший выпуклый многогранник данного числа измерений n. При n = 3 трёхмерный симплекс представляет собой произвольный, в том числе неправильный, тетраэдр. Под двумерным симплексом понимают произвольный треугольник, а под одномерным — отрезок. Нульмерный симплекс есть просто одна точка.[1]
Определение[править | править код]
Симплекс есть выпуклая оболочка n+1 точки n-мерного евклидова пространства, которые предполагаются аффинно независимыми (т.е. не лежат в одной гиперплоскости). Эти точки называются вершинами симплекса.
Связанные определения[править | править код]
- Симплекс называется правильным, если все его рёбра имеют одинаковую длину.
Стандартный симплекс[править | править код]
Стандартный n-симплекс — это подмножество
Его вершинами являются точки:
- e0=(1, 0, …, 0),
- e1=(0, 1, …, 0),
- …
- en=(0, 0, …, 1).
Существует каноническое взаимно-однозначное отображение стандартного n-симплекса в любой другой n-симплекс с координатами вершин
Свойства[править | править код]
- n-мерный симплекс имеет
- В частности, число k-мерных граней в n-симплексе равно биномиальному коэффициенту
- В частности, число граней старшей размерности совпадает с количеством вершин и равно
- В частности, число k-мерных граней в n-симплексе равно биномиальному коэффициенту
- Ориентированный объём n-симплекса в n-мерном евклидовом пространстве можно определить по формуле:
- Определитель Кэли — Менгера позволяет вычислить объём симплекса, зная длины его рёбер:
- где
- Объём правильного n-симплекса с единичной стороной равен
- где
- Радиус
- где
Построение[править | править код]
Если размерность пространства равна n, то через любые n его точек можно провести гиперплоскость, и существуют множества из n+1 точки, через которые гиперплоскость провести нельзя. Таким образом, n+1 — минимальное число таких точек n–мерного пространства, которые не лежат в одной гиперплоскости; эти точки могут служить вершинами n–мерного многогранника.
Простейший n–мерный многогранник с количеством вершин n+1 называется симплексом (принято также название «n-мерный тетраэдр»). В пространствах низшей размерности этому определению соответствуют такие фигуры:
- 0-симплекс (точка) – 1 вершина;
- 1–симплекс (отрезок) – 2 вершины;
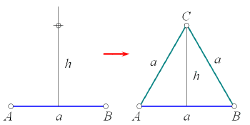
- 2–симплекс (треугольник) – 3 вершины;
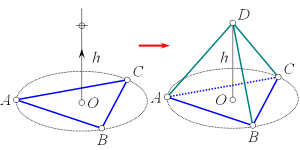
- 3–симплекс (тетраэдр) – 4 вершины.
Все эти фигуры обладают тремя общими свойствами:
- В соответствии с определением, число вершин у каждой фигуры на единицу больше размерности пространства;
- Существует общее правило преобразования фигур низшей размерности в фигуры высшей размерности. Оно заключается в том, что из геометрического центра фигуры строится перпендикуляр в следующее измерение, на этом перпендикуляре строится новая вершина и соединяется рёбрами со всеми вершинами исходного симплекса;
- Как следует из описанной в п. 2 процедуры, любая вершина симплекса соединена рёбрами со всеми остальными вершинами.
Описанная сфера[править | править код]
Вокруг любого n-симплекса можно описать n-сферу.
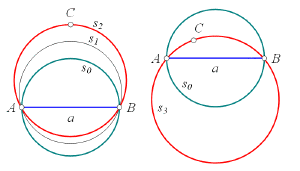
Для 1-симплекса это утверждение очевидно. Описанная 1-сфера будет представлять собой отрезок, совпадающий с самим 1-симплексом, и её радиус будет составлять R = a/2. Добавим к 1-симплексу ещё одну точку и попробуем описать вокруг них 2-сферу.
Построим 2-сферу s0 радиусом a/2 таким образом, чтобы отрезок AB был её диаметром. Если точка С находится за пределами окружности s0, то увеличивая радиус окружности и смещая её в сторону точки С можно добиться того, что все три точки окажутся на окружности. Если же точка С лежит внутри окружности s0, то подогнать окружность под эту точку можно увеличивая её радиус и смещая в сторону, противоположную точке С. Как видно из рисунка, сделать это можно в любом случае, когда точка С не лежит на одной прямой с точками АВ. Не является помехой и несимметричное расположение точки С относительно АВ.
Рассматривая общий случай, предположим, что существует (n–1)-сфера Sn-1 радиуса r, описанная вокруг некоторой (n–1)-мерной фигуры. Поместим центр сферы в начало координат. Уравнение сферы будет иметь вид
Построим n-сферу с центром в точке (0, 0, 0, ... 0, hS) и радиусом R, причём
Подставив в уравнение (2) xn = 0, получим уравнение (1). Таким образом, при любом hS сфера Sn-1 является подмножеством сферы Sn, а именно – её сечением плоскостью xn = 0.
Предположим, что точка С имеет координаты (X1, X2, X3, ..., Xn ). Преобразуем уравнение (2) к виду
и подставим в него координаты точки С:
Выражение в левой части представляет собой квадрат расстояния RC от начала координат до точки C, что позволяет привести последнее уравнение к виду
откуда можно выразить параметр hS:
Очевидно, что hS существует при любых RC, Xn и r, кроме Xn = 0. Это значит, что если точка С не лежит в плоскости сферы Sn–1, всегда можно найти такой параметр hS, что на сфере Sn c центром (0, 0, 0, ..., hS) будет лежать и сфера Sn–1, и точка С. Таким образом, вокруг любых n+1 точек можно описать n–сферу, если n из этих точек лежат на одной (n–1)–сфере, и последняя точка не лежит с ними в одной (n–1)–плоскости.
Применяя последнее по индукции, можно утверждать, что n–сферу можно описать вокруг любых n+1 точек, если они не лежат в одной (n–1)–плоскости.
Число граней симплекса[править | править код]
Симплекс имеет n+1 вершин, каждая из которых соединена рёбрами со всеми остальными вершинами.
Поскольку все вершины симплекса соединены между собой, то тем же свойством обладает и любое подмножество его вершин. Это значит, что любое подмножество из L+1 вершин симплекса определяют его L–мерную грань, и эта грань сама является L–симплексом. Тогда для симплекса число L-мерных граней равно числу способов выбрать L+1 вершину из полного набора n+1 вершин.
Обозначим символом К(L,n) число L–мерных граней в n–многограннике, тогда для n-симплекса
где
В частности, число граней старшей размерности равно числу вершин и равно n+1:
Место физических цветов[править | править код]
Набор всех физических цветов можно интерпретировать как математические векторы в бесконечномерном векторном пространстве, более узко — в гильбертовом пространстве (en:Hilbert_space). Его называют цветовым пространством, Hcolor.
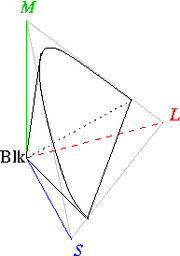
Место физических цветов можно интерпретировать как симплексы (геометрические фигуры, являющаяся n-мерными обобщениями треугольников) в (математическом) конусе, вершины которого — спектральные цвета. Белый цвет (свет) располагается на оси (в точке пересечения оси и основания конуса) (en:Centroid) симплекса, черно-белый — только на оси конуса (внизу — чёрный, вверху — белый, между ними — оттенки серого), и монохроматические цвета, связанные с осью с любой данной вершиной где-нибудь по линии оси от этих вершин в любых плоскостях сечений конусов в зависимости от их яркости. (Максимально яркие цвета спектра располагаются в плоскости наибольшего диаметра сечений конусов, в середине оси)(см. рис.3).
Литература[править | править код]
- Александров П. С., Комбинаторная топология, М. — Л., 1947
- Понтрягин Л. С., Основы комбинаторной топологии, М. — Л., 1947, с. 23—31.
См. также[править | править код]
- Аффинное пространство
- Барицентрические координаты
- Барицентрическое подразделение
- Симплекс-метод
- Симплициальный комплекс
- N-мерная евклидова геометрия
- Теорема косинусов
- Сумма углов треугольника