Астрономия Древней Греции
Астрономия Древней Греции
Под древнегреческой астрономией подразумевается наука тех людей, которые писали на древнегреческом языке, независимо от географического региона: сама Эллада, эллинизированные монархии Востока, Рим, ранняя Византия. Древнегреческая астрономия является одним из важнейших этапов развития не только астрономии как таковой, но и науки вообще. В трудах древнегреческих учёных находятся истоки многих идей, лежащих в основании науки Нового времени. Между современной и древнегреческой астрономией существует отношение преемственности, в то время как наука других древних цивилизаций оказала влияние на современную только при посредничестве греков.
Научный метод древнегреческой астрономии[править | править код]
Главным достижением астрономии древних греков следует считать геометризацию Вселенной, что включает в себя не только систематическое использование геометрических конструкций для представления небесных явлений, но и строгое логическое доказательство утверждений по образцу евклидовой геометрии.
Доминирующей методологией в античной астрономии была идеология «спасения явлений»: необходимо найти такую комбинацию равномерных круговых движений, с помощью которых может быть смоделирована любую неравномерность видимого движения светил. «Спасение явлений» мыслилось греками как чисто математическая задача, и не предполагалось, что найденная комбинация равномерных круговых движений имеет какое-либо отношение к физической реальности. Задачей физики считался поиск ответа на вопрос «Почему?», то есть установление истинной природы небесных объектов и причин их движений исходя из рассмотрения их субстанции и действующих во Вселенной сил; применение математики при этом не считалось необходимым.
Периодизация[править | править код]
Историю древнегреческой астрономии можно условно разделить на четыре периода, ассоциируемых с различными этапами развития античного общества:
- Донаучный период (до VI века до н. э.): становление полисной структуры в Элладе;
- Классический период (VI — IV века до н. э.): рассвет древнегреческого полиса;
- Эллинистический период (III — II века до н. э.): рассвет крупных монархических держав, возникших на обломках империи Александра Македонского; с точки зрения науки особую роль играет птолемеевский Египет со столицей в Александрии;
- Период упадка (I век до н. э. — I век н. э.), ассоциируемый с постепенным угасанием эллинистических держав и усилением влияния Рима;
- Имперский период (II — V века н. э.): объединение всего Средиземноморья, включая Грецию и Египет, под властью Римской империи.
Эта периодизация является достаточно схематичной. В ряд случаев трудно установить принадлежность того или иного достижения к тому или иному периоду. Так, хотя общий характер астрономии и науки вообще в классический и эллинистический период выглядит достаточно различным, в целом развитие в VI — II веках до н. э. представляется более-менее непрерывным. С другой стороны, ряд достижений науки последнего, имперского периода (особенно в области астрономического приборостроения и, возможно, теории) являются ни чем иным, как повторением успехов, достигнутых астрономами эллинистической эпохи.
Донаучный период (до VI века до н. э.)[править | править код]

Представление об астрономических познаниях греков этого периода дают поэмы Гомера и Гесиода: там упоминается ряд звёзд и созвездий, приводятся практические советы по использованию небесных светил для навигации и для определения сезонов года. Космологические представления этого периода целиком заимствовались из мифов: Земля считается плоской, а небосвод — твёрдой чашей, опирающейся на Землю.
Вместе с тем, согласно мнению некоторых историков науки, членам одного из эллинских религиозно-философских союзов того времени (орфикам) были известны и некоторые специальные астрономические понятия (например, представления о некоторых небесных кругах)[1]. С этим мнением, однако, не согласно большинство исследователей.
Классический период (с VI — по IV век до н. э.)[править | править код]
Главными действующими лицами этого периода являются философы, интуитивно нащупывающие то, что в последствии будет названо научным методом познания. Одновременно проводятся первые специализированные астрономические наблюдения, развивается теория и практика календаря; в основу астрономии впервые полагается геометрия, вводится ряд абстрактных понятий математической астрономии; делаются попытки отыскать в движении светил физические закономерности. Получили научное объяснение ряд астрономических явлений, доказана шарообразность Земли. Вместе с тем, связь между астрономическим наблюдениями и теорией ещё недостаточно прочна, слишком велика доля спекуляций, основанных на сугубо эстетических соображениях.
Источники[править | править код]
До нас дошли только два специализированных астрономических труда этого периода, трактаты О вращающейся сфере и О восходе и заходе звёзд Автолика из Питаны — учебники по сферической астрономии, написанные в самом конце этого периода, около 310 года до н. э. [2] К ним примыкает также поэма Феномены Арата из Сол (написанная, впрочем, в первой половине III века до н. э.), где содержится описание древнегреческих созвездий (поэтическое переложение не дошедших до нас трудов Евдокса Книдского (IV век до н. э.) [3].
Вопросы астрономического характера часто затрагиваются в трудах древнегреческих философов: некоторых диалогах Платона (особенно Тимей, а также Государство, Федон, Законы, Послезаконие), трактатах Аристотеля (особенно О Небе, а также Метеорологика, Физика, Метафизика). Труды философов более раннего времени (досократиков) до нас дошли только в очень отрывочном виде через вторые, а то и третьи руки.
Философский фундамент астрономии[править | править код]
В этот период выработались два принципиально различных философских подхода в науке вообще и астрономии в частности. Первый из них зародился в Ионии и поэтому может быть назван ионийским. Для него характерны попытки найти материальную первооснову бытия, изменением которой философы надеялись объяснить все многообразие природы. В движении небесных тел эти философы пытались увидеть проявления тех же сил, что действуют и на Земле. Первоначально ионийское направление было представлено философами города Милета Фалесом, Анаксимандром и Анаксименом. Этот подход нашёл своих сторонников и в других частях Эллады. К числу ионийцев относится Анаксагор из Клазомен, значительную часть жизни проведший в Афинах, в значительной мере уроженец Сицилии Эмпедокл из Акраганта. Своей вершины ионийский подход достиг в трудах античных атомистов: Левкиппа (родом, возможно, также из Милета) и Демокрита из Абдер, явившихся предтечами механистической философии.
Стремление дать причинное объяснение явлений природы было сильной стороной ионийцев. В настоящем состоянии мира они увидели результат эволюции под действием физических сил без привлечения мифических богов и чудовищ. Они были первыми, кого назвали физиками. Однако недостатком учений ионийских натурфилософов была попытка создать физику без математики. Ионийцы не увидели геометрическую основу Космоса.
Второе направление ранней греческой философии можно назвать италийским, поскольку оно получило первоначальное развитие в греческих колониях италийского полуострова. Его основоположник Пифагор основал знаменитый религиозно-философский союз, представители которого, в отличие от ионийцев, видели основу мира в математической гармонии, точнее, в гармонии чисел, стремясь при этом к единению науки и религии. Небесные светила они считали богами. Это обосновывалось следующим образом: боги — это совершенный разум, для них характерен наиболее совершенный вид движения; таковым является движение по окружности, поскольку оно вечное, не имеет ни начала, ни конца и все время переходит само в себя. Как показывают астрономические наблюдения, небесные тела движутся по окружностям, следовательно, они являются богами. Наследником пифагорейцев был великий афинский философ Платон, который полагал весь Космос созданным идеальным божеством по своему образу и подобию. Хотя пифагорейцы и Платон верили в божественность небесных светил, для них не была характерна вера в астрологию: известен крайне скептический отзыв о ней Евдокса, ученика Платона и последователя философии пифагорейцев.
Стремление поисков математических закономерностей в природе было сильной стороной италийцев. Характерная для италийцев страсть к идеальным геометрическим фигурам позволила им первыми предположить, что Земля и небесные тела имеют форму шара и открыть дорогу к приложению математических методов к познанию природы. Однако полагая небесные тела божествами, они практически полностью изгнали с небес физические силы.
Сильные стороны этих двух исследовательских программ, ионийской и пифагорейской, дополняли друг друга. Попытку их синтеза предпринял Аристотель из Стагира. Важнейшим принципом основанной им школы, Ликея, было наблюдение за природой. В значительной степени Аристотелю мы обязаны важнейшим требованием к научной теории: теория должна быть логичной, согласной сама с собой, и вместе с тем она должна соответствовать данным наблюдений. Однако аристотелев синтез ионийского и италийского оказался в значительной мере неудачным. Аристотель как бы рассёк Вселенную по вертикали. Верхняя часть, надлунный мир, в целом соответствовал пифагорейско-платоновскому идеалу совершенной гармонии. Хотя Аристотель не называл небесные светила богами, он полагал их имеющими божественную природу, будучи состоящими из совершенной материи — эфира, для которого характерен наиболее совершенный вид движения — вечное неизменное движение по кругу. Теория подлунного мира, наоборот, напоминает построения философов-ионийцев (доатомистического периода) с их отказом от применения математики к поискам природных закономерностей. Для подлунного мира было характерно движение по вертикальным прямым линиям; такое движение должно иметь начало и конец, что соответствует бренности всего земного.
Практическая астрономия[править | править код]
До нас дошла только фрагментарная информация о методах и результатах наблюдений астрономов классического периода. Исходя из доступных источников, можно предположить, что одним из основных объектов их внимания являлись восходы звёзд, поскольку результаты таких наблюдений можно было использовать для определения времени ночью. Трактат с данными таких наблюдений составил Евдокс Книдский (вторая половина IV века до н. э.); поэт Арат облёк трактат Евдокса в поэтическую форму.
Начиная с Фалеса Милетского интенсивно наблюдались также явления, связанные с Солнцем: солнцестояния и равноденствия. Согласно дошедшим до нас свидетельствам, астроном Клеострат Тенедосский (около 500 г. до н. э.) первым в Греции установил, что созвездия Овна, Стрельца и Скорпиона являются зодиакальными, то есть через них проходит Солнце в своём движении по небесной сфере. Самым ранним свидетельством знания греками всех зодиакальных созвездий является календарь, составленный афинским астрономом Эвктемоном в середине V века до н. э. Тот же Эвктемон впервые установил неравенство времён года, связанное с неравномерностью движения Солнца по эклиптике. По его измерениям, длина астрономической весны, лета, осени и зимы составляет, соответственно, 93, 90, 90 и 92 дней (на самом деле, соответственно, 94,1 день, 92,2 дня, 88,6 дней, 90,4 дня). Гораздо более высокая точность характеризует измерения Каллиппа из Кизика, жившего столетие спустя: по его данным, весна длится 94 дня, лето 92 дня, осень 89 дней, зима 90 дней.
Древнегреческие учёные фиксировали также появления комет, покрытия планет Луной.
Об астрономических инструментах греков классического периода практически ничего неизвестно. Про Анаксимандра Милетского сообщали, что для распознавания равноденствий и солнцестояний он использовал гномон — древнейший астрономический инструмент, представляющий собой вертикально расположенный стержень. Евдокс приписывают и изобретение «паука» — основного конструктивного элемента астролябии[4].
Для исчисления времени днём, по всей видимости, часто использовались солнечные часы. Сначала были изобретены сферические солнечные часы, как наиболее простые. Усовершенствований конструкции солнечных часов также приписывалось Евдокс. Вероятно, это было изобретение одной из разновидностей плоских солнечных часов.
Календарь греков был лунно-солнечным. Среди авторов календарей (так называемых парапегм) были такие знаменитые учёные, как Демокрит, Метон, Эвктемон. Парепегмы часто выбивались на каменных стелах и колоннах, установленных в общественных местах. В Афинах был в ходу календарь, основанный на 8-летнем цикле (согласно некоторым сведениям, введённый знаменитым законодателем Солоном). Значительное усовершенствование лунно-солнечного календаря принадлежит афинскому астроному Метону, который открыл 19-летний календарный цикл:
19 лет = 235 синодических месяцев = 6940 дней.
В течение этого периода времени даты солнцестояний и равноденствий постепенно меняются и одна и та же лунная фаза каждый раз приходится на другую календарную дату, однако по окончанию цикла солнцестояние и равноденствие приходятся на ту же дату, и в этот день имеет место та же фаза Луны, что и в начале цикла. Однако метонов цикл так и не был положен в основу афинского гражданского календаря (а его первооткрыватель удостоился насмешек в одной из комедий Аристофана).
Уточнение метонова цикла произвёл Каллипп, живший примерно через столетие после Метона: он объединил четыре цикла, опустив при этом 1 день. Таким образом, продолжительность каллиппова цикла составила
76 лет = 940 месяцев = 27759 дней.
Год в цикле Каллиппа равен 365,25 суток (такое же значение принято в юлианском календаре). Продолжительность месяца составляет 29,5309 суток, что всего на 22 секунды длиннее его истинного значения. На основе этих данных Каллипп составил собственный календарь.
Космология[править | править код]
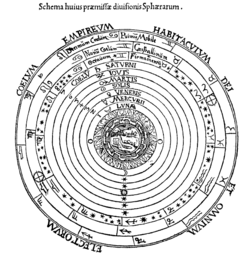
В классическую эпоху возникла геоцентрическая система мира, согласно которой в центре сферической Вселенной находится неподвижная шарообразная Земля и видимое суточное движение небесных светил является отражением вращения Космоса вокруг мировой оси. Её предтечей является Анаксимандр Милетский. В его системе мира содержались три революционных момента: плоская Земля расположена без какой-либо опоры, пути небесных тел являются целыми кругами, небесные тела находятся на различных расстояниях от Земли. Ещё дальше пошёл Пифагор, предположивший, что Земля имеет форму шара. Эта гипотеза поначалу вызвала большое сопротивление; так, среди её противников были знаменитые философы ионийского направления Анаксагор, Эмпедокл, Левкипп, Демокрит. Однако после её поддержки Парменидом, Платоном, Евдоксом и Аристотелем она стала основой всей математической астрономии и географии.
Если Анаксимандр считал звёзды расположенными ближе всего к Земле (далее следовали Луна и Солнце), то его ученик Анаксимен впервые предположил, что звёзды являются самыми далёкими от Земли объектами, закреплёнными на внешней оболочке Космоса. Возникло мнение (впервые, вероятно, у Анаксимена или пифагорейцев), что период обращения светила по небесной сфере растёт с увеличением его расстояния от Земли. Таким образом, порядок расположения светил оказывался таким: Луна, Солнце, Марс, Юпитер, Сатурн, звёзды. Сюда не включены Меркурий и Венера, потому что период их обращения по небесной сфере равен одному году, как и у Солнца. Аристотель и Платон помещали эти планеты сразу за Солнцем. Аристотель обосновывал это тем, что никакая из планет никогда не заслоняла собою Солнце и Луну, хотя обратное (покрытие планет Луной) наблюдалось неоднократно.
Начиная с Анаксимандра, предпринимались многочисленные попытки установить расстояния от Земли до небесных тел. Эти попытки были основаны на спекулятивных пифагорейских соображениях о гармонии мира. Они нашли отражение, в частности, у Платона[5].
Философы-ионийцы полагали, что движением небесных светил управляют силы, аналогичные тем, что действуют в земном масштабе. Так, Эмпедокл, Анаксагор, Демокрит полагали, что небесные тела не падают на Землю, поскольку их удерживает центробежная сила. Италийцы (пифагорейцы и Платон) считали, что светила, будучи богами, движутся сами по себе, как живые существа. Аристотель полагал, что небесные тела переносятся в своём движении твёрдыми небесными сферам, к которым они прикреплены.
Геоцентрическая система мира стала основной космологической моделью вплоть до XVII века н. э. Однако учёные классического периода развивали и другие взгляды. Так, среди пифагорейцев было довольно широко распространено мнение (обнародованное Филолаем Кротонским в конце V века до н. э.), что в середине мира располагается некий Центральный огонь, вокруг которого, наряду с планетами, вращается и Земля, делая полный оборот за сутки. Пифагорейцы выдвинули также мнение, что суточное вращение небосвода объясняется вращением Земли вокруг оси. Это мнение было поддержано и обосновано Гераклидом Понтийским (2-я половина IV века до н. э.). Кроме того, на основании дошедших до нас скудных сведений можно предположить, что Гераклид считал Венеру и Меркурий обращающимися вокруг Солнца, которое, в свою очередь, обращается вокруг Земли. Существует и другая реконструкция система мира Гераклида: и Солнце, и Венера, и Земля вращаются по окружностям вокруг единого центра, причём период одного оборота Земли равен году[6]. В таком случае теория Гераклида являлась органическим развитием системы мира Филолая и непосредственным предшественником гелиоцентрической системы мира Аристарха.
Среди философов были значительные разногласия насчёт того, что находится вне Космоса. Некоторые философы считали, что там располагается бесконечное пустое пространство; по мнению Аристотеля, вне Космоса нет ничего, даже пространства; атомисты Левкипп, Демокрит и их сторонники полагали, что за нашим миром (ограниченным сферой неподвижных звёзд) находятся другие миры. Наиболее близкими к современным были взгляды Гераклида Понтийского, согласно которому неподвижные звёзды — это и есть другие миры, располагающиеся в бесконечном пространстве.
Объяснение астрономических явлений и природы небесных тел[править | править код]
Классический период характеризуется широким распространением спекуляций о природе небесных тел. Анаксагор из Клазомен (V век до н. э.) первым предположил, что Луна светит отражённым светом Солнца и на этой основе впервые в истории дал правильное объяснение природы лунных фаз и солнечных и лунных затмений. Солнце Анаксагор считал гигантским камнем (величиной с Пелопонесс), раскалённым за счёт трения о воздух (за что философ чуть было не подвергся смертной казни, поскольку эта гипотеза была сочтена противоречащей государственной религии). Эмпедокл полагал Солнце не самостоятельным объектом, а отражением на небосводе Земли, освящённой небесным огнём. Пифагореец Филолай полагал, что Солнце является прозрачным сферическим телом, светящееся потому, что она преломляет свет небесного огня; то, что мы видим в качестве дневного светила, это изображение, получающееся в атмосфере Земли. Некоторые философы (Парменид, Эмпедокл) полагали, что яркость дневного неба обусловлена тем, что небосвод состоит из двух полусфер, светлой и тёмной, период обращений которых вокруг Земли составляет сутки, как и период обращения Солнца.
Большое внимание греческих учёных привлекали кометы. Пифагорейцы считали их разновидностью планет. Эти мнения были отвергнуты Аристотелем, который считал кометы (как и метеоры) воспламенением воздуха в верхней части подлунного мира. Причина этих воспламенений заключается в неоднородности окружающего Землю воздуха, наличия в нем легко воспламеняющихся включений, которые вспыхивают из-за передачи тепла от вращающегося над подлунным миром эфира. По мнению Аристотеля, ту же природу имеет и Млечный Путь; вся разница в том, что в случае комет и метеоров свечение возникает из-за нагрева воздуха одной конкретной звездой, в то время как Млечный Путь возникает из-за нагрева воздуха всей надлунной областью. Некоторые пифагорейцы вместе с Энопидом Хиосским считали Млечный Путь выжженной траекторией, по которому некогда обращалось Солнце. Анаксагор полагал Млечный Путь кажущимся скоплением звёзд, находящимся в том месте, где на небосвод падает земная тень. Совершенно правильную точку зрения высказал Демокрит, который полагал, что Млечный Путь — это совместное свечение многих расположенных рядом звёзд.
Математическая астрономия[править | править код]
Главным достижением математической астрономии рассматриваемого периода является концепция небесной сферы. Вероятно, изначально это было чисто умозрительное представление, основанное на соображениях эстетики. Однако позднее было осознано, что явления восхода и захода светил, их кульминации действительно происходят таким образом, будто бы звезды были жёстко скреплены со сферическим небосводом, вращающимся вокруг наклонённой к земной поверхности оси. Таким образом естественно объяснялись основные особенности движений звёзд: каждая звезда всегда восходит в одной и той же точке горизонта, разные звезды за одно и то же время проходят по небу разные дуги, причём чем ближе звезда к полюсу мира, тем меньшую дугу она проходит за одно и то же время. Необходимым этапом работы по созданию этой теории должно было стать осознание того, что размер Земли неизмеримо мал по сравнению с размером небесной сферы, что давало возможность пренебрегать суточными параллаксами звёзд. До нас не дошли имена людей, совершивших эту важнейшую интеллектуальную революцию; скорее всего, они принадлежали к пифагорейской школе. Наиболее раннее дошедшие до нас руководство по сферической астрономии принадлежат Автолику из Питаны (около 310 г. до н. э.). Там доказано, в частности, что точки вращающейся сферы, не лежащие на её оси, при равномерном вращении описывают параллельные круги, перпендикулярные оси, причём за равное время все точки поверхности описывают подобные дуги.
Другим важнейшим достижением математической астрономии классической Греции является введение представления об эклиптике — большом круге, наклонённым по отношению к небесному экватору, по которому совершает своё движение среди звёзд Солнце. Вероятно, это представление было введено знаменитым геометром Энопидом Хиосским, который также сделал и первую попытку измерения наклона эклиптики к экватору (24°).
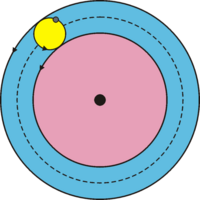
В основу геометрических теорий движения небесных тел древнегреческие астрономы положили следующий принцип: движение каждой планеты, Солнца и Луны является комбинацией равномерных круговых движений. Этот принцип, предложенный Платоном или ещё пифагорейцами, исходит из представления о небесных телах как о божествах, которым может быть присущ только самый совершенный вид движения — равномерное движение по окружности. Как считается, первую теорию движения небесных тел, основанной на этом принципе, предложил Евдокс Книдский. Это была теория гомоцентрических сфер — разновидность геоцентрической системы мира, в которой небесные тела считаются жёстко прикреплёнными к комбинации скреплённых между собой жёстких сфер с общим центром. Усовершенствованием этой теории занимался Каллипп из Кизика, а Аристотель положил её в основу своей космологической системы. Теория гомоцентрических сфер была впоследствии оставлена, так предполагает неизменность расстояний от светил до Земли (каждое из светил движется по сфере, центр которой совпадает с центром Земли). Однако к концу классического периода уже было накоплено значительное количество свидетельств, что расстояния небесных тел от Земли на самом деле меняются: значительные изменения блеска некоторых планет, непостоянство углового диаметра Луны, наличие наряду с полными и кольцеобразных солнечных затмений.
По мнению ван дер Вардена, пифагорейцы ещё доплатоновой эпохи разработали также теории движения планет, основанные на модели эпициклов[7]. Ему даже удалось восстановить некоторые параметры этой ранней теории эпициклов[8]. Достаточно успешными были теории движения внутренних планет и Солнца, причём последняя, по мнению исследователя, была положена в основу календаря Каллиппа. Мнение ван дер Вардена, однако, не разделяется большинством историков науки[9].
Эллинистический период (III — II века до н. э.)[править | править код]
Важнейшую организующую роль в науке этого периода играет Александрийская библиотека и Мусейон. Хотя в начале эллинистического периода возникли две новые философские школы, стоиков и эпикурейцев, научная астрономия уже достигла уровня, который позволил ей развиваться практически не испытывая влияния со стороны тех или иных философских доктрин (не исключено, однако, что религиозные предрассудки, увязанные с философией стоицизма, оказали негативное влияние на распространение гелиоцентрической системы: см. ниже пример Клеанфа).
Астрономия становится точной наукой. Важнейшими задачами астрономов становятся: (1) установление масштабов мира исходя из теорем геометрии и данных астрономических наблюдений, а также (2) построение обладающих предсказательной силой геометрических теорией движения небесных тел. Высокого уровня достигает методика астрономических наблюдений. Объединение античного мира Александром Македонским делает возможным обогащение астрономии Греции за счёт достижений вавилонских астрономов. Вместе с тем, углубляется разрыв между астрономией и физикой, не столь очевидный в предыдущем периоде, а к его концу большое распространение в эллинистическом мире получает пришедшая из Вавилона астрология.
Источники[править | править код]
До нас дошло шесть трудов астрономов этого периода:
- Феномены Евклида (около 300 года до н. э.) — ещё один учебный трактат по сферической астрономии[10];
- О размерах и расстояниях Солнца и Луны, приписываемый Аристарху Самосскому (первая половина III века до н. э.)[11];
- Критика Евдокса и Арата — единственное дошедшее до нас сочинение Гиппарха Никейского (вторая половина II века до н. э.);
- Исчисление песчинок Архимеда (III век до н. э.), посвящённое систематике необходимых в астрономии больших чисел и попутно затрагивающее также ряд других астрономических вопросов[12];
- Превращения в созвездия, приписываемый Эратосфену из Кирены (III век до н. э.) — пересказ мифов, связанных с созвездиями[13];
- О восхождении созвездий по эклиптике Гипсикла из Александрии (II век н. э.), где решается задача об определении времени, которое требуется для восхода или захода каждого знака зодиака; здесь впервые появились заимствованные из Вавилона градусы[14].
Достижения этого периода положены в основу двух элементарных учебников астрономии Гемина (I век до н. э.) и Клеомед (время жизни неизвестно, скорее всего между I веком до н. э. и II веком н. э.), известных под названием Введение в явления. О работах Гиппарха рассказывает Клавдий Птолемей в своём фундаментальном труде — Альмагесте (2-я половина II века н. э.). Кроме того, различные аспекты астрономии и космологии эллинистического периода освещаются в ряде комментаторских работ более поздних периодов.
Практическая астрономия[править | править код]
Календарь. Каллиппово значение длины тропического года (365+(1/4) дней) было положено в основу так называемого зодиакального календаря, или календаря Дионисия (первый годначинался 28 июня 285 г. до н. э.) — солнечного календаря, в котором календарный цикл состоял из трёх лет по 365 дней и одного в 366 дней (как и в юлианском календаре). В 238 году до н. э. базилевс Египта Птолемей III Эвергет сделал неудавшуюся попытку внедрения аналогичного календаря в гражданскую жизнь своей страны [15].
С целью усовершенствования календаря учёные эллинистической эпохи производили наблюдения солнцестояний и равноденствий: длина тропического года равна промежутку времени между двумя солнцестояниями или равноденствиями, делённому на полное число лет. Они понимали, что точность вычисления тем выше, чем больше промежуток между используемыми событиями. Наблюдениями такого рода занимались, в частности, Аристарх Самосский, Архимед Сиракузский, Гиппарх Никейский и ряд других астрономов, имена которых неизвестны.
В библиотеке Ватикана хранится рукопись, в которой приведены данные о величине года согласно измерениям некоторых древних астрономов. В частности, Аристарху приписано два разных значения. Записи сильно искажены, но анализ документа позволил выяснить, что одно из приписанных Аристарху значений близко к продолжительности тропического, другое — звёздного года (соответственно, 365+(1/4)-(15/4868) дней и 365+(1/4)+(1/152) дней)[16]. Поскольку тропический год является промежутком времени между двумя последовательными похождениями Солнца через точку весеннего равноденствия, из неравенства тропического и звёздного года автоматически следует движение точек равноденствий навстречу годичному движению Солнца, то есть предварение равноденствий, или прецессия.
Гиппарх непосредственно убедился в предварении равноденствий, сопоставляя координаты некоторых звёзд, измеренные Тимохарисом в Александрии, с определёнными им самим. По Гиппарху, угловая скорость движения точек равноденствия составляет 1° в столетие. Такое же значение следует из величин звёздного и тропического года по Аристарху, восстановленного из Ватиканских манускриптов (на самом деле, величина прецессии составляет 1° за 72 года).
По определению Гиппарха продолжительность тропического года составляет 365+(1/4)-(1/300) дней (на 6 минут длиннее правильного значения в ту эпоху). Исходя из этого значения Гиппарх внёс очередное усовершенствование в лунно-солнечный календарный цикл: 1 цикл Гиппарха составляет 4 цикла Каллиппа без одного дня:
304 года = 111035 дней = 3760 синодических месяцев.
Возможно, греческие астрономы эллинистической эпохи использовали в своих работах результаты астрономов Месопотамии, ставшие доступными после образования империи Александра Македонского. В пользу этого говорит то, что значение длины синодического месяца, использованное Гиппархом, также встречающееся в вавилонских глиняных таблицах. Возможно, однако, что поток информации был двусторонним: встречающееся в вавилонских глиняных таблицах длина тропического года 365+(1/4)-(5/1188) дней почти наверняка получена исходя из промежутка времени между летними солнцестояниями Гиппарха (135 г. до н. э., о. Родос) и Метона (432 г. до н. э., Афины)[17]. Только что упомянутое значение длины синодического месяца также впервые могло быть получено греческими астрономами школы Аристарха [18]. О наличии потока информации с запада на восток говорит также поддержка вавилонянином Селевком греческой концепции движения Земли.
Угломерные наблюдения. Начиная с IV или даже V века до н. э. в качестве наклона эклиптики к экватору принималось значение 24°. Новое определение этой величины произвёл в конце III века до н. э. Эратосфен в Александрии. Он нашёл, что этот угол составляет 11/83 часть полукруга, или 23°51'. Полученное Эратосфеном значение было использовано Птолемеем в Альмагесте. Однако в нескольких независимых исследованиях было показано, что ряд дошедших до нас образцов античных астрономических и географических работ основан на гораздо более точном значении величины наклона эклиптики к экватору: 23°40'. Истинное значение этой величины в ту эпоху составляло 23°43'.
Александрийские астрономы Тимохарис (~290 год до н. э.) и Аристилл (~260 год до н. э.) производили измерения координат неподвижных звёзд[19]. На протяжении этих десятилетий точность таких наблюдений существенно выросла: от 12' у Тимохариса до 5' у Аристилла[20]. Столь существенный прогресс говорит о наличии в Александрии мощной школы наблюдательной астрономии. Возможно, для записи результатов наблюдений использовалась эклиптическая или экваториальная система координат.
Работу по определению звёздных координат продолжил во второй половине II века до н. э. Гиппарх, составивший первый в Европе звёздный каталог, включивший точные значения координат около тысячи звёзд. Этот каталог до нас не дошёл, но не исключено, что каталог из птолемеева Альмагеста почти целиком является каталогом Гиппарха с пересчитанными за счёт прецессии координатами. При составлении своего каталога Гиппарх впервые ввёл понятие звёздных величин.
Во второй половине III века до н. э. александрийские астрономы также производили наблюдения положений планет (имена этих астрономов неизвестны; все что мы об них знаем, это то, что для датировки своих наблюдений они использовали зодиакальный календарь Дионисия). Побудительные мотивы александрийских наблюдений не вполне ясны[21].
С целью определения географической широты в различных городах проводились наблюдения высоты Солнца во время солнцестояний. При этом достигалась точность порядка нескольких угловых минут, максимально достижимая невооружённым глазом[22].Для определения долготы использовались наблюдения лунных затмений (разность долгот между двумя пунктами равна разности местного времени, когда произошло затмение).
Какие инструменты использовались в ходе этих работ, с достоверностью неизвестно. Вероятно, для наблюдения ночных светил использовалась диоптра, а для наблюдения Солнца — полуденный круг; весьма вероятно также использование астролябии и армиллярной сферы. По словам Птолемея, для определения моментов равноденствий Гиппарх использовал экваториальное кольцо.
Архимед в Исчислении песчинок приводит результаты измерения углового диаметра Солнца, произведённого им с помощью специального прибора: от 1/164 до 1/200 прямого угла (то есть от 32'55" до 27'). По более ранней оценке Аристарха, эта величина составляет 30'; её истинное значение колеблется от 31'28" до 32'37".
Космология[править | править код]
Получив поддержку со стороны стоиков, геоцентрическая система мира продолжала оставаться основной космологической системой в эллинистический период. Сочинение по сферической астрономии, написанное Евклидом в начале III веке до н. э., также основано на геоцентрической точке зрения. Однако в первой половине этого столетия Аристарх Самосский предложил альтернативную, гелиоцентрическую систему мира, согласно которой
- Солнце и звезды неподвижны,
- Солнце расположено в центре мира,
- Земля обращается вокруг Солнца за год и вокруг оси за сутки.
Исходя из гелиоцентрической системы и ненаблюдаемости годичных параллаксов звёзд, Аристарх сделал пионерский вывод, что расстояние от Земли до Солнца пренебрежимо мало по сравнению с расстоянием от Солнца до звёзд. Этот вывод с достаточной долей симпатии приводит Архимед в своём сочинении Исчисление песчинок (одном из основных источников нашей информации о гипотезе Аристарха), что можно считать косвенным признанием гелиоцентрической космологии сиракузским учёным[23]. Возможно, в других своих трудах Архимед развивал иную модель устройства Вселенной, в которой Меркурий и Венера, а также Марс обращаются вокруг Солнца, которое, в свою очередь, движется вокруг Земли (при этом путь Марса вокруг Солнца охватывает Землю)[24].
Большинство историков науки полагает, что гелиоцентрическая гипотеза не получила сколько-нибудь значительной поддержки со стороны современников Аристарха и астрономов более позднего времени. Некоторые исследователи, однако, приводят так косвенных свидетельств о широкой поддержке гелиоцентризма античными астрономами[25]. Тем не менее, известно имя только одного сторонника гелиоцентрической системы: вавилонянин Селевк, 1-я половина II века до н. э.
Стоик Клеанф полагал, что за высказывание идеи о движении Земли Аристарха следовало привлечь к суду. Привёл ли этот призыв к каким-либо последствиям, неизвестно.
Рассматриваемый период отмечен также появлением и других новаторских гипотез. Возникло мнение о возможности собственных движений «неподвижных» звёзд. Во всяком случае, согласно имеющимся свидетельствам, одним из побудительных мотивов Гиппарха при составлении своего звёздного каталога было желание обеспечить астрономов будущих поколений базой данных точных координат звёзд с целью проверки гипотезы о наличии собственных движений звёзд. С этой целью Гиппарх также записал несколько случаев, когда три или более звезды лежат примерно на одной линии.
В I веке до н. э. Гемин обнародовал мнение, что звезды только кажутся лежащими на одной сфере, а на самом деле они располагаются на разных расстояниях от Земли. Есть все основания полагать, что это мнение также зародилось ранее, в III или II веке до н. э., поскольку оно ассоциируется с возможностью существования собственных движений звёзд: наличие таких движений несовместимо с представлением о звёздах как о телах, закреплённых на одной сфере. Оба этих предположения также хорошо гармонирует с гелиоцентрической системой: характерное для геоцентризма представление о неподвижности Земли требует, чтобы звёзды были жёстко закреплены на небесной сфере, поскольку в этом случае суточное вращение неба считается реальным, а не кажущимся, как в случае вращающейся Земли.
Некоторые философы выражали и достаточно архаические взгляды, давно оставленные наукой. Так, последователи Эпикура считали Землю плоской, падающей в «мировую бездну».
Некоторые другие стороны учения эпикурейцев, впрочем, выглядят достаточно передовыми для своего времени. Например, они полагали возможным существование, помимо нашего, и других миров (каждый из которых конечен и ограничен сферой неподвижных звёзд). Их основные соперники, стоики, считали мир единым, конечным и погружённым в бескрайнее пустое пространство. Наибольший интерес представляет точка зрения гелиоцентриста Селевка, полагавшего мир бесконечным.
Попытки установления масштабов Вселенной[править | править код]
Характерные для предыдущего этапа попытки установления расстояний до светил исходя из спекулятивных пифагорейских соображений о гармонии мира не нашли своё продолжение в эллинистический период. В III — II веках до н. э. астрономы сделали ряд оценок расстояний до небесных тел исходя исключительно из теорем евклидовой геометрии и простых физических соображений. Первая из дошедших до нас таких попыток принадлежит Аристарху Самосскому и описана в его труде О размерах и расстояниях Солнца и Луны. Исходя из оценённого им углового расстояния Луны от Солнца в квадратурах (когда с Земли наблюдается половина лунного диска) и физического предположения о свечении Луны отражённым солнечным светом, он оценил отношение расстояний до Солнца и Луны в 19 раз; поскольку угловые размеры обоих светил на небе примерно одинаковы, Солнце оказывается во столько же раз больше Луны по радиусу, то есть в 19 раз. Анализируя далее лунное затмение (привлекая данные о соотношении углового размера лунной тени и видимого радиуса Луны), он вычислил отношение радиусов Солнца и Земли составляет 20:3. Эта оценка примерно в 20 раз меньше истинного значения, что связано с невозможностью точного определения моменты лунной квадратуры. Не исключено, однако, что дошедший до нас трактат О размерах и расстояниях Солнца и Луны написан не самим Аристархом, но является более поздней ученической переработкой оригинального труда самосского учёного под таким же названием, а сам Аристарх полагал, что 19 и 20/3 являются лишь нижними оценками, соответственно, отношения расстояний до Солнца и Луны и отношения радиусов Солнца и Земли[26]. Как бы то ни было, выдающимся результатом Аристарха было установление того факта, что объём Солнца во много раз превышает объём Земли. Возможно, это и привело его к гелиоцентрической гипотезе устройства мироздания.
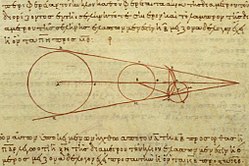
Этими задачам занимался также Гиппарх (работы самого учёного до нас не дошли, мы знаем о них только по упоминаниям других авторов). Сначала для измерения расстояния до Луны он использовал наблюдения солнечного затмения, которое в дваух разных городах наблюдалось в разных фазах. Предполагая, что суточный параллакс Солнца пренебрежимо мал, Гиппарх получил, что расстояние до Луны лежит в пределах от 71 до 83 радиусов Земли. Далее Гиппарх использует, по видимому, метод определения расстояния до Луны, аналогичный использованному ранее Аристархом и предполагает, что суточный параллакс Солнца равен максимальной величине, при которой он неразличим невооружённым взглядом (по Гиппарху, 7', что соответствует расстоянию до Солнца в 490 радиусов Земли). В результате минимальное расстояние до Луны оказалось равным 67 1/3, максимальное 72 2/3 радиусов Земли[27].
Есть основания полагать, что оценки расстояний до небесных тел исходя из ненаблюдаемости их суточных параллаксов делали и другие астрономы[28]; следует напомнить также вывод Аристарха о громадной удалённости звёзд, сделанный исходя из гелиоцентрической системы и ненаблюдаемости годичных параллаксов звёзд.
Определением расстояний до небесных светил занимались также Аполлоний Пергский и Архимед, однако об использованных ими методах ничего не известно. В одной из недавних попыток реконструкций работы Архимеда сделан вывод, что полученное им расстояние до Луны составляет около 62 радиусов Земли и довольно точно измерил относительные расстояния от Солнца до планет Меркурия, Венеры и Марса (основываясь при этом на модели, в которой эти планеты обращаются вокруг Солнца и вместе с ним — вокруг Земли)[29].
К этому следует добавить определение радиуса Земли Эратосфеном. С этой целью он измерил зенитное расстояние Солнца в полдень дня летнего солнцестояния в Александрии, получив результат 1/50 полного круга. Далее, Эратосфену было известно, что в городе Сиене в этот день Солнце находится точно в зените, то есть Сиен находится на тропике. Полагая эти города лежащими точно на одном меридиане и принимая расстояние между ними равными 5000 стадиев, а также считая лучи Солнца параллельными, Эратосфен получил длину земной окружности равной 250000 стадиев. Впоследствии Эратосфен увеличил эту величину до значения 252000 стадиев, более удобного для практических расчётов. Точность результата Эратосфена трудно оценить, поскольку величина использованного им стадия неизвестна. В большинстве современных работ стадий Эратосфена принимается равным 157,5 метров[30] или 185 метров[31]. Тогда его результат для длины земной окружности, в переводе на наши единицы измерения, окажется равным, соответственно, 39690 км (всего на 0,7 % меньше истинного значения), или 46620 км (на 17 % больше истинного значения).
Теории движения небесных тел[править | править код]
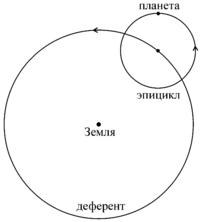
В рассматриваемый период были созданы новые геометрические теории движения Солнца, Луны и планет, в основу которых был положен принцип, согласно которому движение всех небесных тел является комбинацией равномерных круговых движений. Однако этот принцип выступал не в виде теории гомоцентрических сфер, как в науке предшествующего периода, а в виде теории эпициклов, согласно которому само светило совершает равномерное движение по малому кругу (эпициклу), центр которого равномерно перемещается вокруг Земли по большому кругу (деференту). Основы этой теории, как считается, заложил Аполлоний Пергский, живший в конце III — начале II века до н. э.
Ряд теорий движения Солнца и Луны построил Гиппарх. Согласно его теории Солнца, периоды движений по эпициклу и деференту одинаковы и равны одному году, их направления противоположны, в результате чего Солнце равномерно описывает в пространстве окружность (эксцентр), центр которой не совпадает с центром Земли. Это позволило объяснить неравномерность видимого движения Солнца по эклиптике. Параметры теории (отношение расстояний между центрами Земли и эксцентра, направление линии апсид) были определены из наблюдений. Аналогичная теория была создана для Луны, однако в предположении, что скорости движения Луны по деференту и эпициклу не совпадают. Эти теории позволили осуществлять предсказания затмений с точностью, недоступной более ранним астрономам.
Другие астрономы занимались созданием теорий движения планет. Трудность заключалась в том, что в движении планет имелись неравномерности двух видов:
- неравенство относительно Солнца: у внешних планет — наличие попятных движений, у внутренних планет — попятные движения и «привязанность» этих планет к Солнцу;
- зодиакальное неравенство: зависимость величины дуг попятных движений и расстояний между дугами от знака зодиака.
Для объяснения этих неравенств астрономы эпохи эллинизма привлекали сочетание движений по эксцентрическим кругам и эпициклам. Эти попытки были раскритикованы Гиппархом, который, однако, не предложил никакой альтернативы, ограничившись систематизацией доступных в его время данных наблюдений[32].
Период упадка (I век до н. э. — I век н. э.)[править | править код]
В этот период активность в области астрономической науки близка к нулю, зато вовсю цветёт астрология. Как свидетельствуют многочисленные папирусы эллинистического Египта того периода, гороскопы составлялись не на основе геометрических теорий, разработанных греческими астрономами предшествующего периода, а на основе гораздо более примитивных арифметических схем вавилонских астрономов[33]. Философы занимаются главным образом разработкой фундамента астрологии с позиций мистики.
Тем не менее, какой-то элементарный уровень астрономических знаний сохраняется, свидетельством чего является дошедший до нас добротный учебник астрономии Введение в явления Гемина (I век до н. э.). Сохранялась и связанная с астрономией технология, наглядным свидетельством которой является механизм из Антикиферы — калькулятор астрономических явлений, созданный в I веке до н. э.
Заслуживающим упоминания учёным этого периода является склонный к мистицизму философ Посидоний, бывший скорее эклектиком и подражателем учёных более раннего периода, чем оригинальным исследователем.
Имперский период (II — V века н. э.)[править | править код]
Астрономия постепенно возрождается, но с заметной примесью астрологии. В этот период создаются ряд обобщающих астрономических трудов. Однако новый рассвет стремительно сменяется застоем и затем новым кризисом, на этот раз ещё более глубоким, связанным с общим упадком культуры в период крушения Римской империи, а также с радикальным пересмотром ценностей античной цивилизации, произведённым ранним христианством.
Источники[править | править код]
До нас дошли сочинения Клавдия Птолемея (2-я половина II века н. э.):
- Альмагест, затрагивающий почти все аспекты математической астрономии античности — главный источник наших знаний об античной астрономии; содержит знаменитую птолемееву теорию планетных движений;
- Канопская надпись — предварительная версия параметров его планетной теории, высеченная на каменной стеле;
- Подручные таблицы — таблицы планетных движений, составленные на основе изложенных в Альмагесте теорий;
- Планетные гипотезы, где содержится космологическая схема Птолемея.
К астрономии имеют то или иное отношение и другие сочинения Птолемея: Оптика, География и трактат по астрологии Четверокнижие.
В этот период были также написаны два трактата по сферической астрономии, известных под названием Сферика[34]. Один из них является фундаментальным трудом, написанным выдающимся астрономом Менелаем Александрийским (I век н. э.), где изложены основы сферической тригонометрии (внутренней геометрии сферических поверхностей). Второй труд написан Теодосием (I или II век н. э.) и является промежуточным по уровню между трудами ранних авторов (Автолика и Евклида) и Менелая. Теодосию принадлежат также ещё два дошедших до нас труда: О жилищах, где приведено описание звёздного неба с точки зрения наблюдателей, находящихся на разных географических широтах, и О днях и ночах, где рассматривается движение Солнца вдоль эклиптики. Описанию вида звёздного неба посвящён небольшой трактат Астрономия Гигина (I век н. э.)[35].
Вопросы астрономии рассматриваются также в ряде трудов комментаторского характера, написанных в этот период (авторы: Теон Смирнский, II век н. э., Симпликий, V век н. э., Прокл, V век н. э., Цензорин, III век н. э. [36] и др.). Отрывочные сведения по истории античной астрономии содержатся также в трудах энциклопедиста Плиния Старшего, философов Цицерона, Сенеки, Лукреция, архитектора Витрувия, географа Страбона, астролога Манилия. Некоторые астрономические вопросы рассматриваются в трудах механика Герона Александрийского (II век н. э.)
Практическая астрономия[править | править код]
Задачей планетных наблюдений рассматриваемого периода является обеспечение численным материалом теорий движения планет, Солнца и Луны. С этой целью производили свои наблюдения Менелай, Клавдий Птолемей и другие астрономы (по вопросу подлинности наблюдений Птолемея ведётся напряжённая дискуссия[37]). В случае Солнца, основные усилия астрономов по прежнему были направлены на точную фиксацию моментов равноденствий и солнцестояний. В случае Луны, наблюдались затмения (фиксировался точный момент наибольшей фазы и положение Луны среди звёзд), а также моменты квадратур. Для внутренних планет (Меркурия и Венеры), основной интерес представляли наибольшие элонгации, когда эти планеты находятся на наибольшем угловом расстоянии от Солнца. У внешних планет особый упор делался на фиксировании моментов противостояний с Солнцем и их наблюдении в промежуточные моменты времени, а также на изучении их попятных движений. Большое внимание астрономов привлекали также такие редкие явления, как соединения планет с Луной, звёздами и друг с другом.
Производились также наблюдения координат звёзд. Птолемей приводит в Альмагесте звёздный каталог, где, по его утверждению, каждую звезду он наблюдал самостоятельно. Не исключено, однако, что этот каталог почти целиком является каталогом Гиппарха с пересчитанными за счёт прецессии координатами звёзд.
Птолемей описывает несколько астрономических инструментов, бывших в употреблении в его время. Это квадрант, равноденственное кольцо, полуденный круг, армиллярная сфера, трикветрум, а также специальный прибор для измерения углового размера Луны. Герон Александрийский упоминает ещё один астрономический инструмент — диоптру.
Заметным новшеством птолемеева Альмагеста является описание уравнения времени — функции, описывающей отклонение среднего солнечного времени от истинного солнечного времени.
Космология и физика неба[править | править код]
В теории Птолемея предполагался такой порядок следования светил с увеличением расстояния от Земли: Луна, Меркурий, Венера, Солнце, Марс, Юпитер, Сатурн, неподвижные звезды. При этом среднее расстояние от Земли росло с ростом периода обращения среди звёзд; по прежнему оставалась нерешённой проблема Меркурия и Венеры, у которых этот период равен солнечному (Птолемей не приводит достаточно убедительных аргументов, почему он помещает эти проблемы «ниже» Солнца, просто ссылаясь на мнение учёных более раннего периода). Все звезды считались находящимися на одной и той же сфере — сфере неподвижных звёзд. Для объяснения прецессии он был вынужден добавить ещё одну сферу, которая находится выше сферы неподвижных звёзд.
В теории эпициклов, в том числе у Птолемея, расстояние от планет до Земли менялось. Физическую картину, которая может стоять за этой теорией, описал Теон Смирнский (конец I — начало II века н. э.) в дошедшем до нас сочинении Математические понятия, полезные для чтения Платона. Это теория вмонтированных сфер, основные положения которой сводится к следующему. Представим себе две сделанные из твёрдого материала концентрические сферы, между которыми помещена маленькая сфера. Среднее арифметическое радиусов больших сфер является радиусом деферента, а радиус малой сферы — радиусом эпицикла. Вращение двух больших сфер заставит маленькую сферу вращаться между ними. Если поместить на экватор малой сферы планету, то её движение будет в точности таким, как в теории эпициклов; таким образом, эпицикл является экватором малой сферы.
Этой теории, с некоторыми модификациями, придерживался и Птолемей. Она описана в его труде Планетные гипотезы[38]. Там отмечается, в частности, что максимальное расстояние до каждой из планет равно минимальному расстоянию до планеты, следующей за ней, то есть минимальное расстояние до Луны равно минимальному расстоянию до Меркурия и т. д. Максимальное расстояние до Луны Птолемей смог оценить с помощью метода, аналогичного методу Аристарха: 64 радиуса Земли. Это дало ему масштаб всей Вселенной. В результате вышло, что звезды расположены на расстоянии около 20 тысяч радиусов Земли. Птолемей также сделал попытку оценить размеры планет. В результате случайной компенсации ряда ошибок Земля у него оказалась средним по размерам телом Вселенной, а звезды имеющими примерно тот же размер, что и Солнце.
Были и другие попытки придать физический смысл теории эпициклов[39], которые также основывались на геоцентрической системе мира.
Развивались также взгляды, выходящие далеко за рамки этой системы. Так, Птолемей дискутирует с некоторыми учёными (не называя их по имени), которые предполагают суточное вращение Земли. Латинский автор V в. н. э. Марциан Капелла в сочинении Брак Меркурия и филологии описывает систему, в которой Солнце обращается по окружности вокруг Земли, а Меркурий и Венера — вокруг Солнца.
Наконец, в сочинениях ряда авторов той эпохи описаны представления, которые предвосхитили идеи учёных Нового времени. Так, один из участников диалога Плутарха О лике, видимом на диске Луны[40] утверждает, что Луна не падает на Землю из-за действия центробежной силы (подобно предметам, вложенным в пращу), «ведь каждый предмет увлекается естественным ему движением, если его не отклоняет в сторону какая иная сила». В том же диалоге отмечается, что тяготение свойственно не только Земле, но и небесным телам, включая Солнце. Мотивом могла быть аналогия между формой небесных тел и Земли: все эти объекты имеют форму шара, а раз шарообразность Земли связана с её собственной гравитацией, то логично предположить, что и шарообразность других тел во Вселенной связана с той же причиной.
Философ Сенека (I век н. э.) свидетельствует, что в античности были распространены взгляды, согласно которым сила тяготения действует и между небесными телами. При этом попятные движения планет являются лишь видимостью: планеты всегда движутся в одном направлении, ибо если бы они остановились, они бы просто упали друг на друга, а в действительности их удерживает от падения само их движение. Сенека отмечает также возможность суточного вращения Земли.
Плиний и Витрувий описывают теорию, в которой движением планет управляют солнечные лучи «в форме треугольников». Что это означает, очень трудно понять, но возможно, в оригинальном тексте, откуда заимствовали свои описания эти авторы, говорилось о движении планет под действием силы тяготения и инерции[41].
Тот же Сенека излагает одно из мнений о природе комет, согласно которому кометы движутся по очень вытянутым орбитам, будучи видимыми только тогда, когда они достигает нижайшей точки своей орбиты. Он также полагает, что кометы могут возвращаться, причём время между их возвращениями составляет 70 лет (напомним, что период обращения самой известной из комет, кометы Галлея, составляет 76 лет).
Макробий (V век н.э.) упоминает о существовании школы астрономов, предполагавших существование собственных движений звезд, незаметных ввиду огромной удаленности звезд и недостаточного промежутка времени наблюдений[42].
Ещё один древнеримский автор, Манилий (I веке н. э.) приводит мнение, что Солнце периодически притягивает кометы к себе и затем заставляет их удаляться, как и планеты Меркурий и Венера. Манилий также свидетельствует, что в начале нашей эры все ещё жива была точка зрения, что Млечный Путь является совместным свечением многих звёзд, расположенных недалеко друг от друга.
Теории движения небесных тел[править | править код]
Хотя теория движения Солнца, Луны и планет развивалась начиная ещё с эллинистического периода, первая дошедшая до нас теория представлена в Альмагесте Птолемея. Движение всех небесных тел представлено в виде комбинации нескольких движений по большим и малым кругам (эпициклам, деферентам, эксцентрам). Солнечная теория Птолемея полностью совпадает с теорией Гиппарха, о которой мы знаем только из Альмагеста. Значительные новшества содержатся в лунной теории Птолемея, где впервые учтён и смоделирован новый вид неравномерности в движении естественного спутника — эвекция. Недостатком этой теории является преувеличение интервала изменения расстояния от Земли до Луны — почти в два раза, что должно отражаться в изменении углового диаметра Луны, что не наблюдается в реальности.

Наиболее интересной является планетная теория Птолемея (теория бисекции эксцентриситета): каждая из планет (кроме Меркурия) равномерно движется по малому кругу (эпициклу), центр которого совершает движение по большому кругу (деференту), причём Земля смещена относительно центра деферента; самое главное, и угловая, и линейная скорость центра эпицикла меняется при движении по деференту, причём это движение выглядело бы равномерным при наблюдении из некоторой точки (экванта), так что отрезок, соединяющий Землю и эквант делится центром деферента пополам. Эта теория позволяла с большой точностью смоделировать зодиакальное неравенство в движении планет.
Был ли автором теории бисекции эксцентриситета сам Птолемей, неизвестно. По мнению Ван дер Вардена, находящему поддержку в ряде недавних исследований, её истоки следует искать в не дошедших до нас работах учёных более раннего времени[43].
Параметры движения планет по эпициклам и деферентам были определены из наблюдений (хотя до сих пор неясно, не были ли эти наблюдения сфальцифицированы). Точность птолемеевской модели движения Сатурна составляет около 1/2°, Юпитера — около 10' и Марса — более 1°. В случае Венеры и особенно Меркурия ошибки могут доходить до нескольких градусов.
Несмотря на несомненный успех теории экванта с точки зрения предвычисления положений планет, большинство астрономов более позднего времени (Средневековья, эпохи Возрождения) видели её фатальный недостаток в невозможности её интерпретации в терминах физики, в том числе в получившей доминирующее положение теории вмонтированных сфер.
В позднюю античность отмечается также возрождение интереса к теории гомоцентрических сфер ввиду её соответствия философии Аристотеля[44].
Значение древнегреческой астрономии для развития науки[править | править код]
Главными заслугами древнегреческой астрономии можно назвать следующие:
- геометризация Вселенной: за наблюдаемыми на небе явлениями греки видели процессы, происходящие в трёхмерном пространстве;
- последовательно логическая методология;
- разработка важнейших угломерных астрономических приборов;
- введение основных понятий сферической астрономии и развитие сферической тригонометрии;
- открытие шарообразности Земли;
- объяснение природы ряда важнейших астрономических явлений;
- открытие неизвестных ранее явлений (например, прецессия, эвекция);
- вычисление расстояния от Земли до Луны;
- установление малости Земли (и даже, среди гелиоцентристов, малости расстояния от Земли до Солнца) по сравнению с расстоянием до звёзд;
- выдвижение ряда гипотез, получивших поддержку в науке более поздних периодов (особенно гелиоцентрической системы мира);
- создание математических моделей движения Солнца, Луны и планет.
Вместе с тем, значительным недостатком античной астрономии был её разрыв с физикой. С преодоления этого разрыва начала своё развитие наука Нового времени.
Примечания[править | править код]
- ↑ Житомирский, 2001; Веселовский, 1982.
- ↑ См. Матвиевская, 1979.
- ↑ Имеются два издания на русском: в сборниках Небо, наука, поэзия и Историко-астрономические исследования, Вып. XX, 1988.
- ↑ Ван дер Варден, 1959, с. 250.
- ↑ Диалоги Тимей, 86b, Государство, X, 616.
- ↑ Van der Waerden, 1978.
- ↑ Van der Waerden, 1974.
- ↑ Van der Waerden, 1982.
- ↑ Knorr, 1990; Gregory, 2000.
- ↑ См. Матвиевская, 1979.
- ↑ Перевод на русский язык содержится в работе Веселовский, 1961.
- ↑ Перевод на русский язык содержится в сборнике Архимед, Сочинения, М., ГИФМЛ, 1962.
- ↑ Перевод на русский содержится в сборнике Небо, наука, поэзия Online.
- ↑ См. Матвиевская, 1979.
- ↑ Селешников, 1977, с. 50.
- ↑ Rawlins, 1999.
- ↑ Rawlins, 1991.
- ↑ Rawlins, 2002.
- ↑ Goldstein and Bowen, 1991.
- ↑ Maeyama, 1984.
- ↑ Некоторые мнения см. в статьях Van der Waerden, 1984; Житомирский, 2001; Jones, 2006.
- ↑ Rawlins, 2008.
- ↑ Christianidis et al., 2002.
- ↑ Житомирский, 2001.
- ↑ Rawlins, 1987; Van der Waerden, 1987; Russo, 1994, 2004; Идельсон, 1975, с. 175.
- ↑ Rawlins, 2008.
- ↑ Swerdlow, 1969; Toomer, 1974.
- ↑ Rawlins, 2008.
- ↑ Житомирский, 2001.
- ↑ Dutka, 1993.
- ↑ Engels, 1985.
- ↑ Птолемей, Альмагест, IX.2, c. 279.
- ↑ Jones, 1991; Evans. 1998, pp. 344-347.
- ↑ См. Матвиевская, 1979.
- ↑ Гигин, Астрономия.
- ↑ Цензорин, Книга о дне рождения.
- ↑ Ньютон, 1985.
- ↑ Evans, 1998, pp. 384-392.
- ↑ Aiton, 1981.
- ↑ Плутарх, О лике, видимом на диске Луны.
- ↑ Russo, 1994, 2004.
- ↑ Макробий, Комментарий на «Сон Сципиона», книга I, гл. 17, отрывок 16.
- ↑ Duke, 2005.
- ↑ Pingree, 1971.
Ресурсы интернета[править | править код]
- История древнегреческих созвездий.
- Кимелев Ю., Полякова Т. Наука и религия. Глава 1. Античное наследие: от Анаксимандра до Прокла.
- И. В. Лупандин, Лекции по истории натурфилософии (см. лекции 3—8).
- Models for planetary motion: from the homocentric spheres to epicycles and heliocentric orbits (Mogi Vicentini: 3D grapics and videos).
- C.S. McConnell, Models of Planetary Motion from Antiquity to the Renaissance
- Greek_astronomy (MacTutor History of Mathematics archive)
- D. Duke, Ancient Planetary Model Animations
- D. Duke, Six Easy Lectures on Ancient Mathematical Astronomy
- Antikythera Mechanism research project
Литература[править | править код]
Первичные источники
- Арат, «Небесные явления», Историко-астрономические исследования, Вып. XX, 1988. Online
- Аристарх Самосский, «О размерах и взаимных расстояниях Солнца и Луны» Online. Русский перевод входит в статью И. Н. Веселовского «Аристарх Самосский — Коперник античного мира», Историко-астрономические исследования, Вып. VII, 1961 (см. стр. с.20—46).
- Гесиод, «Труды и дни» (содержит древнейшие в греческой литературе упоминания некоторых созвездия). Из сб.: Гесиод, Полное собрание текстов, М., Лабиринт, 2001. Online
- Гигин, «Астрономия», Санкт-Петербург, Изд-во Алетейя, 1997. Online
- «Небо, наука, поэзия. Античные авторы о небесных светилах, об их именах, восходах, заходах и приметах погоды», М., МГУ, 1997. Online
- К. Птолемей, «Альмагест, или Математическое сочинение в тринадцати книгах», М., Наука, 1998. Online
Исследования
- В. А. Бронштэн, «Клавдий Птолемей», М., Наука, 1988. Online
- И. Н. Веселовский, «Аристарх Самосский — Коперник античного мира», Историко-астрономические исследования, Вып. VII, 1961. Online
- И. Н. Веселовский, «Астрономия орфиков», Вопросы истории естествознания и техники, 1982, No2, с. 120-124.
- А. И. Еремеева, Ф. А. Цицин, «История астрономии», М., Изд-во МГУ, 1989.
- С. В. Житомирский, «Античная астрономия и орфизм», М., Янус-К, 2001.
- Н. И. Идельсон, «Этюды по истории небесной механики», М., Наука, 1975. Online
- И. А. Климишин, «Астрономия вчера и сегодня», Киев, Наукова Думка, 1977.
- Г. П. Матвиевская, «Сферика и сферическая тригонометрия в древности и на средневековом востоке», Развитие методов астрономических исследований, Вып.8, Москва-Ленинград, 1979. Online
- О. Нейгебауер, «Точные науки в древности», М., Наука, 1968. Online
- Р. Ньютон, «Преступление Клавдия Птолемея», М., Наука, 1985. Online
- А. Паннекук, «История астрономии», М., Наука, 1966.
- И. Д. Рожанский, «Развитие естествознания в эпоху античности. Ранняя греческая наука о природе», М., Наука, 1979.
- И. Д. Рожанский, «История естествознания в эпоху эллинизма и Римской империи», М., Наука, 1988.
- С. И. Селешников, «История календаря и хронология», М., Наука, 1977.
- П. Таннери, «Первые шаги древнегреческой науки», СПб, 1902.
- Ю. В. Чайковский, «Доплатонова астрономия и Коперник», Историко-астрономические исследования, вып. XXX, М., Наука, 2005, с. 159—200.
- E.J. Aiton, «Celestial spheres and circles», History of Science, Vol. 19, pp. 76—114, 1981. Online
- J. Christianidis, D. Dialetis and K. Gavroglu, «Having a Knack for the Non-intuitive: Aristarchus’s Heliocentrism through Archimedes’s Geocentrism», History of Science, V. 40, Part 2, No. 128, June 2002, 147-168. Статья на сайте журнала
- D.R. Dicks, «Early greek astronomy to Aristotle», Cornell Univ. Press: Ithaca, New York.
- J.L.E. Dreyer, «History of the planetary systems from Thales to Kepler», Cambridge University Press, 1906. PDF
- D. Duke, «The Equant in India: The Mathematical Basis of Ancient Indian Planetary Models», Arch. Hist. Exact Sci., V.59, pp. 563-576, 2005.
- J. Dutka, «Eratosthenes' measurement of the Earth reconsidered», Arch. Hist. Exact Sci., 46, pp. 55-66, 1993. Online
- D. Engels, «The length of Eratothenes' stade», American J. of Philology, V. 106, pp. 298-311, 1985.
- J. Evans, «The history and practice of ancient astronomy», New York: Oxford University Press, 1998.
- J. Evans, «The material culture of Greek astronomy», Journal of the History of Astronomy, V. 30, pp. 238-307, 1999. Online
- A. Gregory, «Plato and Aristotle on eclipses», Journal of the History of Astronomy, V. 31, pp. 245-259, 2000. Online
- T.L. Heath, «Aristarchus of Samos, the ancient Copernicus: a history of Greek astronomy to Aristarchus», Oxford, Clarendon, 1913; reprinted New York, Dover, 1981. PDF
- B.R. Goldstein and A.C. Bowen, «A new view of early Greek astronomy», Isis, V.74(273), pp. 330-340, 1983.
- B.R. Goldstein and A.C. Bowen, «The introduction of dated observations and precise measurement in Greek astronomy», Arch. Hist. Exact Sci., V.43(2), pp. 93-132, 1991.
- A. Jones, «The adaptation of Babylonian methods in Greek numerical astronomy», Isis, V.82(313), pp. 441-453, 1991.
- A. Jones, «Ptolemy’s Ancient Planetary Observations», Annals of science, Vol. 63, No. 3, July 2006, 255-290.
- W.R. Knorr, «Plato and Eudoxus on planetary motions», Journal of the History of Astronomy, V.21, pp. 314-329, 1990. Online
- Y. Maeyama, «Ancient stellar observations : Timocharis, Aristyllus, Hipparchus, Ptolemy — the dates and accuracies», Centaurus, V.27(3-4), pp. 280-310, 1984.
- O. Neugebauer, «The History of Ancient Astronomy: Problems and Methods», Journal of Near Eastern Studies, V.4, No.1, pp. 1-38, 1945. Part 1 Part 2
- O. Neugebauer, «Mathematical methods in ancient astronomy», Bull. Amer. Math. Soc. Volume 54, Number 11, Part 1 (1948), 1013-1041. PDF
- D. Pingree, «On the Greek Origin of the Indian Planetary Model Employing a Double Epicycle», Journal for the History of Astronomy, Vol. 2, pp. 80-85, 1971. Online
- D. Rawlins, «Ancient geodesy: achievements and corruption», Vistas in astronomy, Vol. 28, pp. 255-268, 1985.
- D. Rawlins, «Ancient Heliocentrists, Ptolemy, and the equant», American Journal of Physics, V.55, pp. 235-239, 1987. Online
- D. Rawlins, «Hipparchos' ultimate solar orbit», DIO, V. 1.1, pp. 49-66, 1991. Сайт журнала
- D. Rawlins, «Continued-Fraction Decipherment: Ancestry of Ancient Yearlengths and pre-Hipparchan Precession», DIO, V. 9.1, 1999. Сайт журнала
- D. Rawlins, «Aristarchos and the «Babylonian» System B Month», DIO, V. 11.1, 2002. Сайт журнала
- D. Rawlins, Aristarchos Unbound: Ancient Vision, DIO, V.14, 2008. Статья на сайте журнала
- L. Russo, «The astronomy of Hipparchus and his time: A study based on pre-ptolemaic sources», Vistas in astronomy, V. 38, Pt 2, pp. 207-248, 1994.
- L. Russo, «The forgotten revolution: how science was born in 300 BC and why it had to be reborn», Berlin: Springer 2004.
- N.M. Swerdlow, «Hipparchus on the distance of the sun», Centaurus, V. 14, pp. 287-305, 1969.
- H. Thurston, «Greek mathematical astronomy reconsidered», Isis, V.93, pp. 58-69, 2002.
- H. Thurston, «Early astronomy», New York, Springer-Verlag: 1994.
- G.J. Toomer, «Hipparchus on the distances of the Sun and Moon», Arch. Hist. Exact Sci., 14, pp. 126-142, 1974. Online
- B.L. van der Waerden, The Earliest Form of the Epicycle Theory, Journal of the History of Astronomy, Vol. 5, p.175-185, 1974. Online
- B.L. van der Waerden, «On the motion of the planets according to Heraclides of Pontus», Arch. Internat. Hist. Sci., V. 28(103), pp. 167—182, 1978. Русский перевод
- B.L. van der Waerden, «The Motion of Venus, Mercury and the Sun in Early Greek Astronomy», Archive for History of Exact Sciences, Volume 26(2), pp. 99-113, 1982. Online
- B.L. van der Waerden, «Greek astronomical calendars. III. The calendar of Dionysios», Arch. Hist. Exact Sci., V.29(2), pp. 125-130, 1984. Online
- B.L. van der Waerden, «The heliocentric system in Greek, Persian and Hindu astronomy», in «From deferent to equant: A Volume of Studies in the History of Science in the Ancient and Medieval Near East in Honor of E.S. Kennedy», Annals of the New York Academy of Sciences, Volume 500, June 1987, 525-545. Русский перевод