Рентгеновская оптика преломления

Русский учёный Виталий Васильевич Аристов.

Рентгеновская оптика преломления — оптика (версия Миг), отличающаяся новыми свойствами и характекристиками, обеспечивающая преломление и фокусировку Х-лучей аналогично тонким линзам на базе преломляющих линз, фокусирующих оптических элементов, на базе киноформных преломляющих профилей и оптических элементов призм, полученных из кремния.

Преломляющие Х-излучения оптические элементы и на их базе оптические устройства (микроскопы, телескопы и др.) отличаются новыми свойствами и характкристиками, которые дают возможность получать более высокое разрешение в микроскопии, телескопии по сравнению с существующими рентгенооптическими системаии. Применение, например, рентгеновских преломляющих составных линз является более перспективным направлением в исследованиях атомно-молекулярного и структурного анализа тонких плёнок, изучения скрытых слоёв, синтезированных периодических систем, например, фотонных кристаллов. Применение преломляющих линз и др. элементов рентгеновской оптики для передачи и получения рентгеновских изображений используется в рентгеновской томографии.

Заслуживает внимания внедрение элементов преломляющей Х-оптики в область рентгеновской астрономии. Возможность использования Х-лучей в диапазоне жёсткого рентгеновского излучения позволит изучить и открыть целый ряд проблем доселе не известных. Глубокое зондирование Вселенной в настоящее время вообще отсутствует. Создание телескопов с применением преломляющих Х-лучи Х-линз и преломляющих Х-лучи элементов позволит получить оптические устройства с большими фокусными расстояниями. Одновременно применение Х-линз значительно снижает уровень точности и стоимость изготовления их, по сравнению с элементами отражательной и зонной оптики.

Рис.1. Преломляющая рентгеновская линза с двойным параболическим профилем: (а) единичная линза (один квадрант линзы на изображении удалён); (б) компановка единичных линз в составной набор. Геометрическая апертура линзы $2{R_0} = 1мм$, радиус кривизны в вершине параболы R = 200 мкм. Среднеквадратичная величина шероховатости сформированного профиля 0,1 мкм.

Достигнутые результаты в этом новом, важном направлении принадлежат совместным работам российских и зарубежных учёных (Аристов, Виталий Васильевич) .

Общие сведения

Оптическая рентгеновская оптика развивается и базируется на принципах явлений дифракции c использованием взаимодействия электромагнитной волны в диапазоне Х-излучения с веществом. Вид или тип фокусирующих оптических систем: оптика отражения, дифракционная оптика, рентгеновская оптика преломления, рентгеновские волноводы рассматриваются, рассчитываются исходя из принципов явлений дифракции прохождения Х-лучей в кристаллах, прозрачных для них. Основное большинство видов оптических преломляющих систем как (оптика отражения, дифракционная оптика, рентгеновские волноводы) работают по аналогии с обычными традиционными оптическим системами в диапазоне видимого спектра света. Системы с элементами рентгеновской зеркальной оптики, зонных пластинок Френеля, волноводов а также элементов, преломляюших рентгеновские лучи, подпадают под действие общих принципов преломления эктромагнитных волн.

К нетрадиционным устройсвам рентгеновской оптики следует отнести устройства, к которым относятся элементы брэгг-френелевской оптики. Здесь явление брегговской дифракции на кристаллической структуре сочетается с дифракцией на специально созданой структуре зон Френеля. При этом имеет место эффект угловой дисперсии показателя преломления, что определяет эффект преломления лучей, т.е фокусировку излучения на плоскопараллельном кристалле (но не на поверхностях с криволинейными или радиусными и др. профилями).

Особый интерес вызывают нетрадиционные устройства на базе оптических элементов мультипликативной киноформной оптики. (В области видимого спектра света она малоэффективна и находит узкое приенение). В диапазоне X-излучения в последнее время созданы элементы преломления рентгеновсих лучей, которые находят своё дальнейшее изучение и применение.

Основные понятия рентгеновской оптики преломления

При рентгеновском излучении согласно общей формуле значений коэффициента преломления: $$\!\,n=1-\delta-i\beta$$ вытекает, что вакуум — оптически более плотная среда, чем любое вещество. Значения показателя преломления $\!\,\delta$ прохождении рентгеновских лучей лежат в области между $\,10 ^ {-6}$ и $\, 10 ^ {-5}$ и зависят от квантовой энергии излучения, констант кристаллической решётки и плотности вещества.

Откуда: $$\,\delta =(1-n),$$ $\approx$ ($\!\,10 ^{-5}$ — $\!\,10 ^{-6}$) представляет малую величину и соответственно получаем $\,n \approx 1$ для обычных оптических материалов, о чём свидетельствует отсутствие преломления и дополнительное высокое поглощение проходящих Х-лучей.

В результате проведенных исследований и др. при сравнении характеристик поглащения оказались элементы (атомы) узкого диапазона веществ, у которых преломление преобладает над поглощением. Это химические элементы органические и неорганические с $\!\,Z_{eff}$ $\eqslantless$$\,(12-14)!$ При применении этих материалов ввиду малого декремента затухания электромагнитных волн Показатели преломления формируются с элементами с преломляющими профилями с радиусами кривизны величиной порядка единиц микрона.

Форма преломляющего профиля

Рис.1. Схема преломления X-лучей.

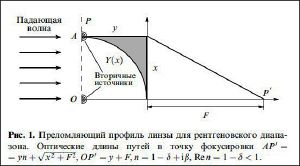
Определение формы преломляющего профиля (см. Рис.1) сводится к нахождению токи (фокуса) фокусировки преломлённых лучей на оптической оси. При определении формулы учитываются только изменения фазы проходящего излучения как это происходит на фазовой зонной пластинке Френеля. При этом любые изменения направлений волновых векторов на отдельных участках проходящей волны сравнительно малы из-за малости декремента преломления. Приняв это следует, что преломляющий прфиль, эквивалентен профилю тонкой линзы. Вывод уравнения профиля из вышеуказанного получен из условия падения волны на входную поверхность фокусирующего элемента в виде плоскости. $\,PO$ (Рис.1). При падении плоской волны на входную плоскость фокусирующего элемента согласно принципу Гюйгенса-Френеля необходимо учитывать возбуждаемые вторичные источники излучений электромагнитных волн. Из рисунка видим, что при фокусировке в точке $\,P^{\prime}$ длина оптического пути от плоскости $\,P$ до точки $\,P^{\prime}$ равна для всех источников на профиле $\,AP^{\prime}$ = $\,OP^{\prime}$ для произвольной точки $\,A$. Неравенство $\,R_{en}$ = $\,1$—$\,\beta$$\,$$\,A$ позволяет компенсировать оптические длины пути любой свободной точки $\,A$. Откуда, согласно идеальная форма преломляющих поверхностей для рентгеновских линз в допущении параксиальной оптики приближается к параболтческой (см.Рис.1):

$$\begin{equation} \label {rentgen} Y(x) = \frac{x^2}{L\pi}{2F\lambda}\left[1-\left(\frac{x}{2F} \right)^2\right] \end{equation}$$

Откуда:

• $\,AP^{1}$ = $\,yn$ + ${\sqrt{x^2+F^2}}$,
• $\,OP^{1}$ =$\,y$ + $\,F$,
• $\!\,n=1-\delta-i\beta$,
• $\,R_{en}$ = $\,1$—$\,\beta$$\,$$\,A$.

Из $\eqref {rentgen}$ также выводится зависимость между радиусом кривизны параболического профиля и его фокусным расстоянием в следующем виде: $$\,R$$= $\,2F\beta$. Из уравнения (1) и других фокусное расстояние F в пределах от 10см до 1м достигается при радиусе кривизны R единичного преломляющего профиля с размерами в диапазоне от 1мкм до 10мкм при оптимальных значениях декремента показателя преломления $\,\delta =(1-n)$, $\approx$ ($\!\,10 ^{-5}$ — $\!\,10 ^{-6}$), что представляет малую величину и соответственно в итоге получаем $\,n \approx 1$ для обычных оптических материалов, о чём свидетельствует отсутствие преломления и дополнительное высокое поглощение проходящих Х-лучей.

Влияние точностей технологических поверхностей Х-линз

Точность формирования расчётных преломляющих поверхностей Х-линз определяет получение на фокальной плоскости вид и размер кружка нерезкости фокусируемого изображения.

Получение случайных отклонений линз от , например, рассчётной параболы, приводящие к сбоям фаз проходящей волны, сказывается на интенсивность в точке $\,(I)$ фокусировкии — единичной линзы (для Фотосенсора — это пиксел) с непредвиденным от расчётов отклонением профиля. Данное явление описывается выражением: $$\begin{equation} \label {pixsel} \,I = I{exp}\left[-\left(\frac{\pi\triangle Y}{L\pi} \right)^2\right] \end{equation}$$ $\,(I)$ — это точка, где происходит фокусировка в идеальных поверхностях.

Виды случайных отклонений

Виды случайных отклонений зависимосят от:

• Вида случайных отклонений линз от , например, рассчётной параболы, который ведёт к сбоям фаз проходящей волны и происходят за счёт аппоксимации параболы (см.Рис.1) при наборе прямолинейных отрезков. . В этом случае имеют место систематические сбои фаз из-за различия оптических путей волны в параболических и аппроксиммирующих профилях. И в данном случае для сохранения когерентости результатов действия волн, прошедших через участки аппрокимирующего профиля, необходимо соблюдение критерия Рэлея, урвнение запишется:

$$\begin{equation} \label {Reley} \,\triangle \Phi\ = \frac{l\pi}{L\pi} \eqslantless\frac{\pi}{4} \end{equation}$$ Откуда величина $\,l$, равная для всех отрезков разбивки профиля не зависит от порядкового номера отрезка и из $\eqref {Reley}$ следует, что шаг разбиения не должен быть больше френелевского радиуса для конкретной единичной линзы.

Технологические погрешности создания преломляющих поверхностей в конечном случае приводят к размытию каустики в виде потерь интенсивности и деформации фокального пятна.

• От точности создания линз от длины волны:

Точность образования и расположение преломляющих профилей линз определяется величиной $\,\lambda/\pi(n-1)$. В оптике видимых лучей света величина длин волн находится в диапазоне от микронов до десятых долей микрона. Для стекла с n=1,5 $\,\lambda$=0,5мкм считается достаточной величина точности в 0,3мкм. В рентгеновском диапазоне эти величины больше и составляют 10-100мкм и используются при изготовлении преломляющих профилей Х-линз с величинами длин сдвига фаз для выбранных материалов. При таких допусках при современной технологии нет проблем для изготовления Х-линз. Например, такая точность достигается при получении асферических поверхностей для оптических элементов проекционной рентгенолитографии, использующей необычные технологии и методы контроля.

Материалы рентгеновских оптических элементов

Выбор материалов для изготовления рентгеновских преломляющих элементов (линз, призм, пластинок) зависит от степени прозрачности, величины допустимых поглощений и искажений исследуемого изображения, получаемого на фокальной поверхности, величины дисперсии. Например, кристаллы кремния обладают самой низкой дисперсией при максимальном коэффициенте преломления электромагнитных лучей (n=3,4!).

Учёт поглощения электромагнитной волны в преломляющем элементе (линзе) получают по величине коэффициента линейного поглощения $\,\mu$ , когда не учитываются фазосдвигающие свойства материала. Однако более доказанным критерием выбора материалов служит соотношение преломляющих показатеоей с поглощающими как:

$$\begin{equation} \label {dispersia} \,N_o=\frac{1}{\mu{L\pi}} \end{equation}$$

Применяемое число $\,N_o$ просто выражается через декременты показателя преломления и факторы атомного рассеяния. Эта величина $\,N_o$ также определяет величину фокального кружка нерезкости (пятна) при фокусировке плоской волны — дифракционного предела линзы (исследуемого объекта).

На основании базы данных $\eqref {dispersia}$ , где имеются основные параметры для фазосдвигающих материалов рентгеновских линз преломления $\,N_o$ и $\,L_\pi$, на основании атомных факторов рассеяния рассчитаны и определён диапазон энергий излучения, составляющий до 100кэВ для всех химических элементов и более 60-ти соединений..

В результате приняты материалы для изготовления преломляющих Х-линз — это кремний и полимерные материалы. Эти материалы обеспечивают:

• Формирование единичных линз с радиусом кривизны $R \eqslantless1$мкм с применением освоенных технологий в микроэлектронике;
• Отсутствие внутреннего несовершенства в структкрах кремния, т.е. потерь интенсивности фокусируемых точек(пятен)..

Виды оптических кремниевых элементов (Х-линз)

Короткофокусные параболические X-линзы

Рис.2. Короткофокусные параболические линзы из кремния, полученные методом глубокого фотоанодного травления.

Параметры преломляющих поверхностей (профилей) линз являются параболоиды вращения. У них радиусы кривизны R=0,35мкм, апертура А=8мкм, оптическая ось перпендикулярна к поверхности образующей пластины. Линза представляет квадратную матрицу, где число элементов образует площадь, которая перекрывает сечение падающего пучка Х-лучей. Вычокая прозрачность, малое поглощение потока лучей делат эти линзы сходные, аналогичными с линзами видимого диапазона электромагнитных волн световых лучей.

Свойства созданных единичных линз было изучено и проверено на источнике излучения ESRF (Гренобль, Франция) в диапазоне энергий 17-30 кэВ. Изображение регистрировалось в цифровой камере высокого разрешения. Размер фокального пятна не превышал 0,7мкм.

Матрица линз — представляет совершенный двумерный оптический элемен, подтвердиший возможности совершенства фотонных кристаллов, например, кремниевых!

Составные преломляющие Х-линзы из кремния

Рис.1. Преломляющая рентгеновская линза с двойным параболическим профилем: (а) единичная линза (один квадрант линзы на изображении удалён); (б) компановка единичных линз в составной набор — получение сборной X-линзы. Геометрическая апертура линзы $2{R_0} = 1мм$, радиус кривизны в вершине параболы R = 200 мкм. Среднеквадратичная величина шероховатости сформированного профиля 0,1 мкм.

Принцип работы сборной Х-линзы

‎Составные преломляющие Х-линзы из кремния подтверждают аддитивные свойсва, присущие обычным линзам.

Набор преломляющих линз, прилегающих друг с другом и плотно собранных с кратностью $\,p$ и его оптическую силу рассчитывается по формуле:

В случае, когда фокусные расстояния идентичных линз одинаковы $(\,F_o = F)$ из $\eqref {nabor lins}$, вытекает: $$\begin{equation} \label {nabor lins} \,D = \frac{1}{F_o}= \sum_{i=1}^p \frac{1}{F_i} \end{equation}$$

$$\begin{equation} \label {bolshoy nabor lins} \,F_o = \frac{F}{p} \end{equation}$$

В случае большого набора $\,p$ происходит существенное сокращение фокусного расстояния $\,F$

При наборе комплектов сборных линз при их изготовдении все препятствия устраняются при учёте свойств аддитивности набора. При этом становится несущественной разница в случае применения относительно точных профилей: парболических, цилиндрических или сферических.

Планарные линзы на основе кремния

Планарные параболические линзы

Файл:Mikroscopia kristalov.jpg

Применение планарных линз на примере прохождения Х-лучей в кристаллах

Технология прецизионной литографии получения планарных линз на плоскоской подложке позволяет формировать профиль единичных линз с малыми радиусами кривизны в случае, когда требуется расположить оптическую ось линзы в плоскости подложки. При этом преломляющий профиль создаётся на последующих этапах создания линзы даже в случае необходимости удаления материала пластины кремния или его нанесения осаждением. При удалении материала применяется способ его глубокого травления, например, плазмохимическим методом снятия материала

Параболические линзы из кремния — это набор преломляющих прфилей с:

• одинаковым фокусным расстоянием 1метр (E=17,4кэВ),
• апертурой А=100мкм,
• увеличенной кратностью единичных линз в ряду от p=1 до p=8,
• соответствующим увеличением радиуса кривизны R от 3,3 до 26,4 мкм.

Глубина рельефа до 100мкм достигнута глубоким плазмохимическим травлением. Увеличение рельефа достигается за счёт увеличения радиуса кривизны парабол по глубине профиля. За счёт механической стыковки планарных линз форимруеется удвоение глубины рельефа планарных линз.

Основным свойством параболических профилей является то, что оптический путь Х-луча и значит сдвиг фазы при прохождении его нескольких линз остаётся постоянным. Увеличение числа линз в ряду с постоянной апертурой компенсируется соответствующим изменением радиуса кривизны. При этом оптическая сила ряда p есть суперпозиция последовательного действия единичных линз и соответственно равна для всех рядов. Откуда последовательная компановка единичных линз с фокусными расстояниями $\,F_o>\!\!>L$ суммарного продольного размера любого набора показывает аддитивность оптических сил аналогично оптическим силам видимого спектра.

Фокусировка и коллимация Х-лучей преломляющими Х-линзами

Одним из главных элементов всех фокусирующих систем — получение минимального размера величины, фокусируемой предметной точки, на фокальной плоскости, например, экрана. Аналогично, в рентгенографии, особенно, это является одной из главных задач создания и применения преломляющи Х-лучи, фокусирующих рентгеновских устройсв — элементов. В данном случае преломляющие линзы, построенные на основах дифракционной или зеркальной оптики, обладают рядом ценных преимуществ по сравнению с обычными оптическими элементами. Дополнительно изучено и показано в , что по аналогии с тонкими линзами условия преломления электромагнитных волн применимы также для Х-линз (важно), и что в собранных Х-линзах с набором элементов большой кратности соблюдается соотношение $\,L \cong F_o$.

Наименьшие размеры, как известно, фокальное пятно получает в условиях лучевой оптики при применении микрозонда, где $\,a>\!\!> b$ и $\,b \cong F_o$. Примененяя данные схемы на синхронных источниках с $\,a =(40-60)$м, а $F_o \approx (0,5-1)$м, уменьшение схемы источника может составить 100-120. Откуда, если размеры источника s<=80-100мкм, становится возможным достижение субмикронного фокального пятна с размерами менее 1мкм. Для линз с коротким фокусным расстоянием 0,1-0,2 становиться возможным дальнейшее ументшение фокального пятна. В данном случае обеспечивается нанофокусировка Х-излучения. В этом нанометровом диапазоне фокусировок линейчатые фокальные пятна с использованием планарных линз лежат в пределах половины их ширины. Сама длина линейчатого пятна задаётся глубиной пофиля планарной линзы (50-200мкм,), протяженность области каустики вдоль оптической оси может достичь до 5-10мм (важный показатель для получения стереоизображения 3D). Измеряемые значения как правило значительно больше.

Преломляющие Х-линзы могут надёжно использоваться как длинофокусные устройства.

Получение изображений в реальном и фурье-пространствах

Файл:X-linsa v fluoreszentnom nanoscope +.jpg

Рис.1,Cхема флюоресцентного наноскопа с использованием Х-линзы, преломляющей Х-лучи

Фокусирующие элементы могут передавать рентгеновские изображения в реальном (видимом) пространстве объектов в виде стереоизображений 3D. В данном случае важно при создании методов рентгеноскопии, когда пространственное разрешение фиксируется предельным разрешением сфокусированного объекта на субмикронном атомно-молекулярном уровне. Эти методы уже с 1980 годов реализованы, но в диапазоне «мягких» Х-волн при использовании зонных пластинок Френеля и рентгеновской зеркалной оптикой. В данном случае, например, получают двумерные рентгеновские изображения при использовании мягких Х-лучей с энергией 1-1,5кэВ, где глубина поглощения менее 1мкм, что не на много больше разрешения, т.е. 20-100нм.

В диапазоне жёсткого излучения (мощностью от 6-10 до 100кэВ), где работают преломляющие линзы, глубина поглощения достигает величин больших значенийй разрешения самих линз. Кроме того надо учесть, что преломляющие Х-линзы, дающие субмикронное фокальное пятно, имеют глубину резкости примерно 0,1—1см. И любое двумерное их оптическое изображение есть проекционное с деталями, которыые накладываются по ходу луча. Откуда, наиболее целесообразнее получить объективную оценку, применив способы томографии, компьютерной томографии, магнитно-резонансной томографии., получая изображение в трёхмерном пространстве (3D).

Для получения рентгеновских изображений в действительном пространстве сейчас в основном применяют преломляющие линзы, рассмотренные выше, с параболическим аксиально симметричным профилем. Имеются и другие Х-линзы с другими рассчётными профилями. В настоящее время опережающее развитие получает безлинзовая компьютерная микроскопия в томографии, где происходит форимрование трёхмерных изображенй структуры объектов (3D). Сейчас созданы нанотомографы с разрешением 200нм. Для повышения разрешения трехмерных изображений величиной в 25-50нм предполагается применение в топографии методов преобразований сигналов изображений нанообъектов — спектров дифракции в фурье-пространстве (с последующими преобразованиями сигналов — дискретизациия, калибровка, восстановление их при АЦП и т.д. с выдачей в стерео пространстве изображений на экране монитора). Флюоресцентная наноскопия с разрешением 1-10 нм отличается тем, что в разных участках объекта периодически создаются видимые раздельно флуоресцирующие молекулы и наночастицы. Лазер (рентгеновский) обеспечивает такое их возбуждение, которое достаточно не только для регистрации их неперекрывающихся изображений, но и для обесцвечивания уже зарегистрированных флуоресцирующих молекул. При этом десятки тысяч кадров с зарегистрированными изображениями одиночных молекул и наночастиц (в виде пятен диаметром порядка длины волны света флуоресцении, умноженной на увеличение микроскопа), обрабатываются на компьютере для поиска координат центров пятен и создания изображения объекта по миллионам вычисленных координат центров пятен, соответствующих координатам индивидуальных флуоресцирующих молекул и наночастиц. При этом применяемые две цифровые, размещённые под углом, с высоким разрешением камеры, улавливая светящиеся окрашенные в RGB цвета микрочастицы (молекулы, атомы) при формировании стереоизображений окрашивают их в нужный цвет.

Область применения

• Линзы
• Офтальмология
• Микроскопы
• Телескопы
• Волноводная оптика
• Световод
• Контактные линзы
• Объективы
• Радиоастрономия
• Радары
• Бинокли
• Матрица (фото)(Микролинзы)

См. также

• Оптические материалы
• Рентгеновская оптика
• Рентгеновская оптика и монокристаллы
• Кремний
• Волновод (керамика)
• Кварц
• Дифракция Брэгга