Волна
| Механика сплошных сред | ||||||||||

| ||||||||||
Сплошная среда
| ||||||||||
Волна́ — изменение состояния среды (возмущение), распространяющееся в этой среде и переносящее с собой энергию. Другими словами: "…волнами или волной называют изменяющееся со временем пространственное чередование максимумов и минимумов любой физической величины, например, плотности вещества, напряжённости электрического поля, температуры.,[1][2]
Более правильное определение: Волна — это явление распространения в пространстве с течением времени возмущения физической величины.
Независимо от природы волны перенос энергии осуществляется без переноса вещества; последнее может возникнуть лишь как побочный эффект. Перенос энергии — принципиальное отличие волн от колебаний, в которых происходят лишь «местные» преобразования энергии. Волны же, как правило, способны удаляться на значительные расстояния от места своего возникновения. По этой причине волны иногда называют «колебанием, оторвавшимся от излучателя». И все же возможен вариант волн, где происходит волновой перенос именно материи, а не только энергии. Это возможность материального излучения, имеющего волновые изменения количества излучаемой материи. Такие волны способны распространяться сквозь абсолютную пустоту.
Большинство волн по своей природе являются не новыми физическими явлениями, а лишь условным названием для определённого вида коллективного движения. Так, если в объёме газа возникла звуковая волна, то это не значит, что в этом объёме появились какие-то новые физические объекты. Звук — это лишь название для особого скоординированного типа движения тех же самых молекул. То есть большинство волн — это колебания некоторой среды. Вне этой среды волны данного типа не существуют (например, звук в вакууме).
Имеются, однако, волны, которые являются не «рябью» какой-либо иной среды, а представляют собой именно новые физические сущности. Так, электромагнитные волны в современной физике — это не колебание некоторой среды (называвшейся в XIX веке эфиром), а самостоятельное, самоподдерживающееся поле, способное распространяться в вакууме. Аналогично обстоит дело и с волнами вероятности материальных частиц.
Некоторые явления также называют волнами, однако каждая из них обладают собственной спецификой. Так, с определёнными оговорками, говорят про: температурные волны, волны вероятности электрона и других частиц, волны горения, волны химической реакции, волны плотности реагентов, волны плотности транспортных потоков.
Отметим, что явления, выглядящие как волны, но не способные сами распространяться (как, например, песчаные дюны), волнами не являются.
Характеристики волны[править | править код]
Временна́я и пространственная периодичности[править | править код]
В отличие от стационарного колебания волны имеют две основные характеристики:
- временну́ю периодичность — скорость изменения фазы с течением времени в какой-то заданной точке, называемую частотой волны
- пространственную периодичность — скорость изменения фазы в определённый момент времени с изменением координаты — длина волны
Временная и пространственная периодичности взаимосвязаны, что отражено в законе дисперсии, который определяет, как именно волны будут выглядеть и распространяться. В упрощённом виде для линейных волн эта зависимость имеет следующий вид:
Строго говоря, это равенство справедливо только для гармоничных волн.
Интенсивность волны[править | править код]
О силе волны судят по её амплитуде. В отличие от колебания амплитуда волны — скалярная величина.
Но для количественной характеристики переносимой волной энергии используется вектор плотности потока энергии
Классификации волн[править | править код]
Имеется множество классификаций волн, различающиеся по своей физической природе, по конкретному механизму распространения, по среде распространения и т. п.
Волны можно классифицировать:
- Океанские поверхностные волны, которые являются волнениями, которые образуются посредством воды;
- Электромагнитные волны (Радиоволны, инфракрасные лучи, видимый свет, ультрафиолетовые лучи, рентгены, и гамма-лучи, которые составляют электромагнитную радиацию), которые могут перемещаться без среды, в вакууме со скоростью света, равной 299 792 458 м\с в вакууме;
- Звук — механическая волна, которая образуется в газах, жидкости, в средах с твердыми частицами и плазме;
- Волны движения, то есть, образование различных потоков (волн) автомашин, и др., которые могут быть смоделированы как кинематические волны, что впервые представлено сэром М. J. Lighthill[3];
- Сейсмические волны в землетрясениях, из которых есть три типа, названные S, P, и L;
- Гравитационная волна — гравитационное излучение, излучение гравитационных волн, или волн тяготения, неравномерно движущимися массами (телами).[3]
Или гравитационная волна — возмущение гравитационного поля, порождающего изменение формы («ряби») пространства-времени, распространяющаяся предположительно со скоростью света.
- Волны гравитации — волны, произведенные в жидкой среде или в интерфейсе между сопряжениями двух элементов (СМИ) (например, атмосфера и океан), которые могут быть восстановлены силами гравитации или состоянием плавучести.
- Инерционные волны, которые происходят во вращающихся жидкостях и восстанавливаются эффектом Coriolis;
- Волны в плазме.
По отношению к направлению колебаний частиц среды, в которой распространяется волна, выделяют:
По виду фронта волны (поверхности равных фаз): |
|
На Рис.1 показаны периодические волны, которые характеризуются гребнями (максимумы) и впадинами (минимумами), и могут обычно категоризироваться как или продольные или поперечные.
- Поперечные волны — волны с направлением колебаний, перпендикулярным к вектору распространения волны; примером служат волны в области электромагнитных волн. *Продольные волны — те, которые имеют колебания, параллельные вектору распространения волны; например, большинство звуковых волн.
Когда объект подпрыгивает на ряби в водоёме, то вектор движения точек волны происходит по орбитальной траектории. Появляющаяся рябь — не простые поперечные синусоидальные волны.
Все волны имеют общее поведение со множеством стандартных ситуаций.
По демонстрируемым волнами физическим проявлениям их можно разделить на:
- линейные волны — волны с небольшой амплитудой, свойства которых описываются простыми линейными зависимостями;
- нелинейные волны — волны с большими амплитудами, что приводит к возникновению совершенно новых эффектов и существенно изменяет характер уже известных явлений;
- солитоны (уединённые волны);
- ударные волны или нормальные разрывы.
По постоянству во времени различают:
- одиночная волна — короткое одиночное возмущение (солитоны);
- волновой пакет — это ряд возмущений, ограниченных во времени с перерывами между ними. Одно беспрерывное возмущение такого ряда называется цуг волн. В теории волновой пакет описывается как сумма всевозможных плоских волн, взятых с определёнными весами. В случае нелинейных волн, форма огибающей волнового пакета эволюционирует с течением времени;
- Подобно сложным колебаниям, волновые цуги и негармонические волны могут быть представлены в виде суммы (суперпозиции) синусоидальных волн разных частот. Когда фазовые скорости всех этих волн одинаковы, то вся их группа (волновой пакет) движется с одной скоростью.
- Если же фазовая скорость волны зависит от её частоты w, наблюдается дисперсия — волны различных частот идут с разной скоростью. Нормальная, или отрицательная дисперсия тем больше, чем выше частота волны. За счёт дисперсии, например, луч белого света в призме разлагается в спектр, в каплях воды — в радугу. Волновой пакет, который можно представить как набор гармонических волн, лежащих в диапазоне w0 ± Dw, из-за дисперсии расплывается. Его форма — огибающая амплитуд компонент цуга — искажается, но перемещается в пространстве со скоростью vгр, называемой групповой скоростью. Если при распространении волнового пакета максимумы волн, его составляющих, движутся быстрее огибающей, фазовая скорость сигнала выше групповой: сф > vгр. При этом в хвостовой части пакета за счёт сложения волн возникают все новые максимумы, которые передвигаются вперёд и пропадают в его головной части. Примером нормальной дисперсии служат среды, прозрачные для света — стёкла и жидкости.
- В ряде случаев наблюдается также аномальная (положительная) дисперсия среды, при которой групповая скорость превышает фазовую: vгр > сф, причём возможна ситуация, когда эти скорости направлены в противоположные стороны. Максимумы волн появляются в головной части пакета, перемещаются назад и исчезают в его хвосте.
По постоянству во времени различают:
- одиночная волна — короткое одиночное возмущение (солитоны);
- волновой пакет — это ряд возмущений, ограниченных во времени с перерывами между ними. Одно беспрерывное возмущение такого ряда называется цуг волн. В теории волновой пакет описывается как сумма всевозможных плоских волн, взятых с определёнными весами. В случае нелинейных волн, форма огибающей волнового пакета эволюционирует с течением времени;
- Подобно сложным колебаниям, волновые цуги и негармонические волны могут быть представлены в виде суммы (суперпозиции) синусоидальных волн разных частот. Когда фазовые скорости всех этих волн одинаковы, то вся их группа (волновой пакет) движется с одной скоростью.
- Если же фазовая скорость волны зависит от её частоты w, наблюдается дисперсия — волны различных частот идут с разной скоростью. Нормальная, или отрицательная дисперсия тем больше, чем выше частота волны. За счёт дисперсии, например, луч белого света в призме разлагается в спектр, в каплях воды — в радугу. Волновой пакет, который можно представить как набор гармонических волн, лежащих в диапазоне w0 ± Dw, из-за дисперсии расплывается. Его форма — огибающая амплитуд компонент цуга — искажается, но перемещается в пространстве со скоростью vгр, называемой групповой скоростью. Если при распространении волнового пакета максимумы волн, его составляющих, движутся быстрее огибающей, фазовая скорость сигнала выше групповой: сф > vгр. При этом в хвостовой части пакета за счёт сложения волн возникают все новые максимумы, которые передвигаются вперёд и пропадают в его головной части. Примером нормальной дисперсии служат среды, прозрачные для света — стёкла и жидкости.
- В ряде случаев наблюдается также аномальная (положительная) дисперсия среды, при которой групповая скорость превышает фазовую: vгр > сф, причём возможна ситуация, когда эти скорости направлены в противоположные стороны. Максимумы волн появляются в головной части пакета, перемещаются назад и исчезают в его хвосте.
Происхождение волн[править | править код]
Волны могут генерироваться различными способами.
- Генерация локализованным источником колебаний (излучателем, антенной).
- Спонтанная генерация волн в объёме при возникновении гидродинамических неустойчивостей. Такую природу могут иметь, например, волны на воде при достаточно большой скорости ветра, дующего над водной гладью.
- Переход волн одного типа в волны другого типа. Например, при распространении электромагнитных волн в кристаллическом твёрдом теле могут генерироваться звуковые волны.
Общие свойства волн[править | править код]
Распространение в однородных средах[править | править код]
При распространении волн изменения их амплитуды и скорости в пространстве и времени зависят от свойств анизотропности среды, сквозь которую проходят волны.
Чаще волны в некоторой среде затухают, что связано с диссипативными процессами внутри среды. Но в случае некоторых специальным образом подготовленных метастабильных сред амплитуда волны может, наоборот, усиливаться (пример: генерация лазерного излучения).
На практике монохроматические волны встречаются очень редко. Поэтому наряду с фазовой скоростью волны используется и понятие групповой скорости, то есть скорость «центра тяжести» волнового пакета.
Групповая и фазовая скорости совпадают только для линейных волн. Для нелинейных волн групповая скорость может быть как больше, так и меньше фазовой скорости. Однако когда речь идёт о скоростях, близких к скорости света, проявляется заведомое неравноправие между групповой и фазовой скоростями. Фазовая скорость не является ни скоростью движения материального объекта, ни скоростью передачи данных, поэтому она может превышать скорость света, не приводя при этом ни к каким нарушениям теории относительности. Групповая же скорость характеризует скорость движения сгустка энергии, переносимой волновым пакетом, и потому не должна превышать скорость света. Однако при распространении волны в метастабильной среде удаётся в определённых случаях добиться групповой скорости, превышающей скорость света.
Поскольку волна переносит энергию и импульс, то её можно использовать для передачи информации. При этом возникает вопрос о максимально возможной скорости передачи информации с помощью волн данного типа (чаще всего речь идёт об электромагнитных волнах). При этом скорость передачи информации никогда не может превышать скорости света, что было подтверждено экспериментально даже для волн, в которых групповая скорость превышает скорость света.
Пространственные размеры волны[править | править код]
Когда говорят о пространственном размере волны, то имеют в виду размер той области пространства, где амплитуду колебания нельзя считать (в рамках рассматриваемой задачи) пренебрежимо малой. Большинство волн могут, теоретически, обладать сколь угодно большим размером, как в направлении движения, так и поперёк него. В реальности же все волны обладают конечными размерами. Продольный размер волны, как правило, определяется длительностью процесса излучения волны. Поперечный же размер определяется рядом параметров: размером излучателя, характером распространения волны (например, плоская, сферически расходящаяся волна и т. д.).
Некоторые виды волн, в частности, солитоны, являются ограниченными волнами по построению.
Поляризация волн[править | править код]
Если в поперечной волне нарушается симметрия распределения возмущений (например, напряжённость электрического и магнитного полей в электромагнитных волнах) относительно направления её распространения, то мы имеем дело с поляризованной волной. В продольной волне поляризация возникнуть не может, так как распространение возмущения всегда совпадает с направлением распространения волны.
Подробней на эту тему см. статью «Поляризация волн».
Взаимодействие с телами и границами раздела сред[править | править код]
Если на пути волны встречается какой-либо дефект среды, тело или граница раздела двух сред, то это приводит к искажению нормального распространения волны. В результате этого часто наблюдаются следующие явления:
Конкретные эффекты, возникающие при этих процессах, зависит от свойств волны и характера препятствия.
Наложение волн[править | править код]
Излучения с разной длиной волны, но одинаковые по физической природе, могут взаимодействовать друг с другом, интерферировать. При этом могут возникнуть следующие частные эффекты:
- стоячие волны;
- бегущие волны;
- биения — периодическое уменьшение и увеличение амплитуды суммарного излучения;
- волновой пакет — образующиеся максимумы амплитуды имеют прерывистое распределение (волновой пакет Гаусса);
- эффект Доплера — изменение длины и амплитуды волн при движении приёмника или источника излучения.
Конечный результат проявления от встречи волн зависит от их свойств: физической природы, когерентности, поляризации и т. д.
Виды волн[править | править код]
Классифицированные волны можно в основном представить как:
- Синусоидалные волны;
- Смодулированные волны;
- Постоянные волны;
- Вибрирующие волны;
- Гармонические волны.
Математические описания волн[править | править код]
Математическое описание волн основывается на представлении о них, как о пространственно распространяющихся колебаниях, и в общем виде записывается:
Более определённый вид уравнения зависит от типа волны.
Синусоидалные волны[править | править код]
Математически, самая основная волна — волна синуса (или гармоническая волна или синусоида), с амплитудой u описанный уравнением:
- A — полуамплитуда волны, половина амплитуды: пика-к-пику, часто называемой просто амплитуда или максимальное расстояние от самого высокого пункта волнения в среде (гребень) к пункту равновесия в течение одного цикла волны. На иллюстрации направо, это — максимальное вертикальное расстояние между основанием и волной;
- x — абсцисса (вектор распространения волны),
- t — координата времени,
- k — пространственная частота,
- ω — временная частота,
- φ — погашение фазы.
Единицы полуамплитуды зависят от типа волны — волн, выраженных через амплитуду как расстояние, например в метрах, от звуковых волн, выраженных через давление и электромагнитных волн, выраженных через амплитуду электрической области (вт/метр).
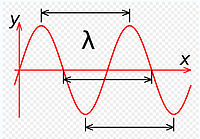
- λ — длина волны — расстояние между двумя последовательными гребнями (или впалдинами), измеряется в метрах.
- k — пространственная частота волны в радианах аналогиччно при подсчёте из расстояния единицы длины в метрах, может быть связана с длиной волны отношением:
Период T — время для одного полного цикла колебания волны. Частота f (также часто обозначаемый как ν) — число периодов в единицу времени (в секунду) и измерена в герц. Они связаны:
Вообще, частота и период волны — аналоги.
Угловая частота ω представляет частоту в радианах в секунду. Это связано с частотой:

Длина волны может быть полезным понятием, даже если волна не является периодической. Например, в океанской волне, приближающейся к берегу, показанному на фигуре, поступающая волна взаимодействует с переменной местной длиной волны, которая зависит частично от глубины морского дна по сравнению с высотой волны. Анализ волны может быть основанным на сравнении местной длины волны с местной водной глубиной.[5]
Хотя произвольные формы волны образуются неизменно без потерь в линейных инвариантных во времени системах, без присутствия дисперсии. Волна синуса — уникальная форма, которая создаётся неизменной, облегчая анализировать фазы и амплитуды.,.[6][7] Функция синуса является периодической, таким образом волна синуса или синусоида имеют длину волны в месте и периоде одновременно.,[8][9] Синусоида и расстояния определяются навсегда, тогда как в физических ситуациях мы обычно имеем дело с волнами, которые существуют для ограниченного диапазона в месте и в промежутке времени.
Уравнение волны[править | править код]
Уравнение волны — частичное отличительное уравнение, которое описывает развитие волны в течение долгого времени в среде, где волна формируется на той же самой скорости, независимой от длины волны и независимый от амплитуды.[10] Общие решения основаны на принципе Дахамэля.[11]
Скорость v зависит от среды, через которую перемещается волна.
Общее решение для уравнения волны в одном измерении давалось d'Alembert; это известно как формула d’Alembert:.[12]
Эта формула представляет две формы волны, движущейся через среду в противоположных направлениях:
- F—в положительном x направлении,
- Г—в отрицательном x направлении (Формы F и Г функционально произвольны).
Смодулированные волны[править | править код]
Амплитуда волны может быть постоянной или может быть смодулирована, чтобы измениться со временем и/или положением. Схему изменения в амплитуде называют «конвертом волны». Математически, смодулированная волна может быть написана в форме:,[13],[14][15]
Постоянная волна[править | править код]
Постоянная волна, известная как постоянная волна, является волной, которая остаётся в постоянном положении. Это явление произходит тогда, когда среда перемещается в противоположном направлении к волне, или это может возникнуть в постоянной среде в результате вмешательства между двумя волнами, движущихся в противоположных напправлениях.
Сумма двух противоположно движущихся волн (равной амплитуды и частоты) создает постоянную волну. Постоянные волны обычно возникают, когда граница блокирует дальнейшее распространение волны, таким образом вызывая отражение волны, и поэтому вводя противоположнодвижущуюся волну. В экстремальных точках, две противоположных волны находятся в антифазе и отменяют друг друга, производя узел. На полпути между двумя узлами есть антиузел, где две противоразмножающихся волны увеличивают друг друга максимально. Нет в среднем положении никакого чистого распространения энергии {среднее число}.
См. также: Акустический резонанс, Резонатор Helmholtz, и труба — предмет.
Вибрационные волны[править | править код]
Скорость волны, распространняющаяся по вибрирующему множеству волн («веренице») (v) напрямую пропорциональна квадратному корню напряженности множества волн («вереницы») (T) по линейной массовой плотности (μ):
где (μ) — линейная плотность — масса на единицу длины «вереницы».
Гармоническая волна[править | править код]
Изменение колеблющейся величины
В любой другой точке, расположенной на расстоянии
Лучи волны[править | править код]
Лучом волны называется линия, направление которой совпадает с направлением потока энергии в этой волне в каждой её точке. Например, плоской волне (см. раздел «Классификация волн») соответствует пучок параллельных прямых лучей; сферической волне — радиально расходящийся пучок лучей.
Расчёт формы лучей при небольшой длине волны — по сравнению с препятствиями, поперечными размерами фронта волны, расстояниями до схождения волн и т. п. — позволяет упростить сложный расчёт распространения волны. Это применяется в геометрической акустике и геометрической оптике.
Направления исследований волн[править | править код]
- Получение точных решений для различных нелинейных волн.
- Распространение волн в случайных средах.
См. также[править | править код]
Ссылки[править | править код]
- ↑ Горелик Г. С. Колебания и волны. Введение в акустику, радиофизику и оптику. — М.: Гос. издат. ф.— м. лит-ры, 1959, с. 144.
- ↑ http://en.wikipedia.org/wiki/Wave
- ↑ http://bse.sci-lib.com/article012647.html
- ↑ Paul R Pinet. op. cit.. p. 242. ISBN 0763759937. http://books.google.com/books?id=6TCm8Xy-sLUC&pg=PA242.
- ↑ Paul R Pinet. op. cit.. p. 242. ISBN 0763759937. http://books.google.com/books?id=6TCm8Xy-sLUC&pg=PA242.
- ↑ Mischa Schwartz, William R. Bennett, and Seymour Stein (1995). Communication Systems and Techniques. John Wiley and Sons. p. 208. ISBN 9780780347151. http://books.google.com/books?id=oRSHWmaiZwUC&pg=PA208&dq=sine+wave+medium++linear+time-invariant&lr=&as_brr=3&ei=u69cSpuKNZDKkASph-GaBw.
- ↑ See Eq. 5.10 and discussion in A. G. G. M. Tielens (2005). The physics and chemistry of the interstellar medium. Cambridge University Press. pp. 119 ff. ISBN 0521826349. http://books.google.com/books?id=wMnvg681JXMC&pg=PA119. ; Eq. 6.36 and associated discussion in Otfried Madelung (1996). Introduction to solid-state theory (3rd ed.). Springer. pp. 261 ff. ISBN 354060443X. http://books.google.com/books?id=yK_J-3_p8_oC&pg=PA261. ; and Eq. 3.5 in F Mainardi (1996). «Transient waves in linear viscoelastic media». in Ardéshir Guran, A. Bostrom, Herbert Überall, O. Leroy. Acoustic Interactions with Submerged Elastic Structures: Nondestructive testing, acoustic wave propagation and scattering. World Scientific. p. 134. ISBN 9810242719. http://books.google.com/books?id=UfSk45nCVKMC&pg=PA134.
- ↑ Aleksandr Tikhonovich Filippov (2000). The versatile soliton. Springer. p. 106. ISBN 0817636358. http://books.google.com/books?id=TC4MCYBSJJcC&pg=PA106.
- ↑ Seth Stein, Michael E. Wysession (2003). An introduction to seismology, earthquakes, and earth structure. Wiley-Blackwell. p. 31. ISBN 0865420785. http://books.google.com/books?id=Kf8fyvRd280C&pg=PA31.
- ↑ Michael A. Slawinski, Klause Helbig (2003). «Wave equations». Seismic waves and rays in elastic media. Elsevier. pp. 131 ff. ISBN 0080439306. http://books.google.com/books?id=s7bp6ezoRhcC&pg=PA134.
- ↑ Jalal M. Ihsan Shatah, Michael Struwe (2000). «The linear wave equation». Geometric wave equations. American Mathematical Society Bookstore. pp. 37 ff. ISBN 0821827499. http://books.google.com/books?id=zsasG2axbSoC&pg=PA37.
- ↑ Karl F Graaf (1991). Wave motion in elastic solids (Reprint of Oxford 1975 ed.). Dover. pp. 13‒14. http://books.google.com/books?id=5cZFRwLuhdQC&printsec=frontcover.
- ↑ Christian Jirauschek (2005). FEW-cycle Laser Dynamics and Carrier-envelope Phase Detection. Cuvillier Verlag. p. 9. ISBN 3865374190
- ↑ Fritz Kurt Kneubühl (1997). Oscillations and waves. Springer. p. 365. ISBN 354062001X
- ↑ Mark Lundstrom (2000). Fundamentals of carrier transport. Cambridge University Press. p. 33. ISBN 0521631343
- ↑ Chin-Lin Chen (2006). «§ 13.7.3 Pulse envelope in nondispersive media». Foundations for guided-wave optics. Wiley. p. 363. ISBN 0471756873. http://books.google.com/books?id=LxzWPskhns0C&pg=PA363.
- ↑ Chin-Lin Chen (2006). «§ 13.7.3 Pulse envelope in nondispersive media». Foundations for guided-wave optics. Wiley. p. 363. ISBN 0471756873. http://books.google.com/books?id=LxzWPskhns0C&pg=PA363.
- ↑ Stefano Longhi, Davide Janner (2008). «Localization and Wannier wave packets in photonic crystals». in Hugo E. Hernández-Figueroa, Michel Zamboni-Rached, Erasmo Recami. Localized Waves. Wiley-Interscience. p. 329. ISBN 0470108851. http://books.google.com/books?id=xxbXgL967PwC&pg=PA329.
Литература[править | править код]
- Крауфорд Ф. Берклеевский курс физики, том 3, Волны.
- Ландау Л. Д., Лифшиц Е. М. Курс теоретической физики, том 6, Гидродинамика.издание?
- Уизем, Дж. Линейные и нелинейные волны — М.: Мир, 1977.
- Физика. Большой энциклопедический словарь/Гл. ред. А. М. Прохоров. — 4-е изд. — М.: Большая Российская энциклопедия, 1999. — С. 85—88. ISBN 5-85270-306-0 (БРЭ)