Масштабное измерение
Масштабное измерение ― измерение, рассматриваемое как степень свободы в теории бесконечной вложенности материи, характеризующее расположение всех известных объектов Вселенной на масштабной лестнице уровней материи. С помощью SPФ-симметрии можно осуществить переход от некоторой системы на одном уровне материи к подобной системе на другом уровне материи, при этом изменение размеров системы сопровождается изменением по крайней мере ещё двух параметров, например, массы и скорости процессов.[1]
Отсюда следует, что масштабное измерение отличается от обычных трёхмерных пространственных измерений, и является особой степенью свободы. При изучении носителей материи, олицетворяющих масштабное измерение, выявляется фрактальность космических систем, их самоподобие, иерархичность устройства и вложенность малых систем в большие, подобие уровней материи. Переход от некоторого уровня материи ко всё более низшим уровням обнаруживает глубину пространства-времени — объекты уменьшаются по массе и размерам, а скорость локального течения времени с точки зрения внешнего наблюдателя увеличивается.
В той области исследований, в которой используются масштабные преобразования и пространственные измерения, масштабное измерение может изучаться геометрическими методами и тем самым входит в предмет геометрии. Идея масштабного измерения окончательно оформилась в трудах Роберта Олдершоу, Сергея Сухоноса и Сергея Федосина.
История[править | править код]
Поисками и исследованиями перспектив новых пространственных измерений занимались многие учёные и философы. Елена Блаватская писала:
|
Как видно, Блаватская под четвёртым измерением полагала не просто новое пространственное измерение, а измерение, опосредованное свойствами материи, которые могут стать осознанными и принятыми в будущем.
Пётр Успенский при описании свойств четвёртого измерения исходил из того, что движение точки за свои пределы оставляет след в виде линии; аналогичное перемещение линии даёт след в виде поверхности; перемещение поверхности в направлении, не связанном с самой поверхностью, даёт трёхмерное тело. Значит, перемещение трёхмерного тела в некотором не трёхмерном направлении должно приводить к следу в виде четырёхмерного тела. Успенский также обращает внимание на то, что линия есть некоторое множество точек, поверхность — множество линий, а тело можно представлять как множество поверхностей, связанных друг с другом. Следовательно, четырёхмерное тело должно состоять из множества связанных каким-то образом в единое целое трёхмерных тел.
С другой стороны, линия ограничена точками на концах и задаёт расстояние между ними, поверхность ограничена линиями и точками и определяет расстояние между этими линиями и точками (примером является круг с центром и окружностью), а трёхмерное тело ограничено поверхностями, линиями и точками с определённым расстоянием между ними. Тогда границами четырёхмерного тела могут быть трёхмерные тела, а также вероятно поверхности, линии и точки. Успенский также пишет:
|
В физике идея дополнительных пространственных измерений используется в теориях объединения фундаментальных взаимодействий. Одной из первых таких теорий была теория Калуцы — Клейна (Теодор Калуца, 1921 г.), пытавшейся соединить электромагнетизм и гравитацию. Ввиду ненаблюдаемости четвёртого пространственного измерения в нашем мире Оскар Клейн в 1926 г. предположил, что это измерение компактифицировано и имеет очень малый размер. В теории струн используются 10-мерное и 26-мерное пространство-время, и дополнительные измерения также подвергаются компактизации.
Историко-философский анализ использования понятий пространственной размерности показывает, [4] что самые ранние модели Вселенной были в виде яйца (нульмерная размерность). Эти модели сменились вначале ленточной одномерной моделью Древнего Египта , в которой Вселенная выглядит как вытянутая река Нил. Над этой Вселенной на столбах простирается такое же лентообразное небо в виде плоской крыши. Звезды в небе выглядят как шляпки гвоздей, которые вколочены в небесную крышу снизу. Затем появились двухмерные модели античности — Земля у Гомера (VIII в. до н. э.) уподоблялась выпуклому щиту, со всех сторон была окружена рекой-океаном и накрыта звёздным куполом, а средневековая плоская Земля стояла на китах или слонах, и также была накрыта звёздным куполом. Модель Вселенной Птолемея (II в. н. э.), была практически двухмерной, в ней вокруг Земли по эпициклическим орбитам вращаются планеты и звезды (последние находятся на вращающемся сферическом куполе). В настоящее время в науке господствует гелиоцентрическая модель Солнечной системы и трёхмерная модель Вселенной западноевропейской цивилизации. Таким образом, происходит наращивание размерности пространства во всех моделях мира и всех областях представлений о нём. Последнее подтверждается историей живописи, когда древние рисунки одномерны, в средневековье двухмерны, и лишь в эпоху Возрождения они приобретают третье измерение. С начала двадцатого века художники стали предпринимать попытки показать новое четвёртое измерение. Наиболее впечатляющих результатов это достигло в картинах Маурица Эшера и Сальвадора Дали. Аналогично живописи путь от ленточного пространства к трехмерному проделала и архитектура. Одной из наиболее известных попыток прорваться в архитектурное четырёхмерие можно считать творчество Ле Корбюзье. Указанные примеры из живописи, космологии и архитектуры неоспоримо доказывают, что за последние пять тысяч лет цивилизация прошла путь развития от одномерного пространства сознания к трёхмерному, и в настоящее время находится в состоянии перехода в четырёхмерное.
Современный подход[править | править код]
Существуют разные точки зрения на масштабное измерение, подчёркивающие те или иные свойства находящихся в нём объектов и тем самым характеризующие само масштабное измерение.
Например, Фурнье Д'Альба считал,[5] что отношение линейных размеров звезды и атома, а также отношение длительностей их однотипных процессов, выражается числом 1022. Юн Пио Янг путём сравнения атомов и галактик находит для коэффициентов подобия по размерам и времени значение порядка 1030.[6] Тем самым подчёркивается различие хода времени на разных уровнях материи, как следствие свойств масштабного измерения.
С точки зрения геометрии, описывающей лишь пространственные формы, понятие «Масштабное измерение» является некоторой интерпретацией понятия «Четвёртое пространственное измерение». Можно представить себе некоторую четвёртую ось пространства, двигать вдоль неё трёхмерное тело и считать, что четырёхмерное тело есть весь набор форм, которые приняло трёхмерное тело при перемещении вдоль четвёртой оси пространства. Аналогично движение точки (нулевое измерение) даёт линию (одно измерение); движение линии, параллельное самой себе, очерчивает плоскую фигуру (два измерения); движение плоской фигуры в направлении вектора, не лежащего в плоскости фигуры, приводит к объёмному телу. В отличие от такого подхода, масштабное измерение обладает дополнительным свойством — геометрические объекты не просто движутся в пространстве для образования четвёртого измерения, но при этом ещё могут менять свой масштаб. То есть трёхмерное тело может менять свой размер (объём) при движении вдоль масштабной оси, аналогично может изменяться площадь фигуры и толщина линии. Как любая ось системы координат в пространстве-времени, масштабная ось отличается от всех других осей своим направлением, и в геометрии этого достаточно. Для физических систем удобно полагать, что направление масштабной оси показывает в сторону увеличения масштабов, а противоположное направление устремлено в глубь пространства.
Четвёртое измерение является весьма сложным для воображения. Один из способов увидеть его проявление — представить себя уменьшающимся в размере и наблюдающим окружающее пространство с объектами в нём. Другой вариант — выделить в пространстве объём наблюдения и постоянно уменьшать его размер. Процесс будет бесконечным, и несмотря на то, что за пределами масштаба, ограниченного пределами планковских величин, квантовая физика не представляет того, что происходит, мы не можем утверждать, что там нет пространства. Такое уменьшение объёма наблюдения открывает, кроме того, особенности пространства, трудно воспринимаемые сознанием, а именно — бесконечность пространства в бесконечном количестве точек. Так как все 5 видимых не вооруженным глазом (или представляемых образно) измерения (включая время) имеют бесконечную протяжённость, то и предполагать конечность четвёртого измерения со стороны малых масштабов пока нет оснований.
В философии понятие пространства определяется как форма существования материи, обладающей свойством протяжённости, а время — как форма существования материи, обладающей свойством длительности существования. В теории относительности элементарное событие описывается пространственными координатами и моментом времени, в который рассматриваемый объект находится в данной пространственной точке. Введение в рассмотрение временной оси как эквивалентной оси системы отсчёта стало возможным лишь благодаря ограниченности скорости света, поскольку длина отрезка временной оси определяется произведением скорости света на промежуток времени и должна быть конечна. Из этого следует, что временная ось по своему происхождению не тождественна ни одной пространственной оси, а физическое пространство-время не эквивалентно какому-либо n-мерному геометрическому пространству. Масштабное измерение, как и время, занимает особое положение при определении полной физической системы отсчёта, необходимой в каждом случае для решения теоретических и практических задач.
Масштабная относительность[править | править код]
Роберт Олдершоу рассматривает дискретную самоподобную масштабную относительность, обнаруживаемую в масштабном измерении, как фундаментальный принцип симметрии природы, расширяющий принцип общей относительности при изучении физических систем.[7] К основным уровням в наблюдаемым мире Олдершоу относит атомные, звёздные и галактические уровни материи, причём в природе должны быть пока ещё не наблюдаемые уровни материи на микро масштабах и на мега масштабах.
Между уровнями материи согласно Олдершоу могут быть установлены связи в виде одних и тех же коэффициентов подобия по размерам и времени, равным Λ = 5,2∙1017, а также коэффициента подобия по массе X = ΛD = 1,7∙1056, где показатель степени D = 3,174. Это приводит к различию гравитационных постоянных на разных уровнях материи — постоянная сильной гравитации на уровне атомов, обычная гравитационная постоянная для уровня звёзд, и предполагается существенно уменьшенное значение гравитационной постоянной для уровня галактик:
Олдершоу считает необходимым расширить принцип относительности в том смысле, что физические законы должны записываться таким образом, чтобы они не зависели не только от положения в геометрическом трёхмерном пространстве, от времени, от ориентации, состояния движения, но и от положения системы отсчёта на дискретной масштабной лестнице материи, то есть от выбора уровня материи на масштабной оси. По его мнению, если между уровнями материи выполняется точное космологическое самоподобие (через неизменность коэффициентов подобия для всех уровней), физические законы и относительные постоянные на данных уровнях должны быть одинаковы.
Волновая интерпретация[править | править код]
Сергей Сухонос вводит в рассмотрение масштабную ось (М-ось) как особое, четвёртое пространственное измерение, и располагает на ней все объекты Вселенной.[8] При этом он обнаруживает, что в расположении групп объектов существует упорядоченность, соответствующая логарифмическому закону увеличения их размеров.[9] В связи с этим Сухонос делает предположение о том, что наблюдаемое распределение групп объектов, имеет своей причиной гармонические колебания в четырёхмерном пространстве, которые порождают узлы — трёхмерные устойчивые системы. Для обоснования такой точки зрения рассматриваются собственные колебания в виде стоячих волн в объектах различной размерности, когда на длине объекта всегда укладывается целое число волн.
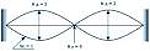
Одномерный случай для струны, зажатой с двух сторон, показан на рисунке 1. Струна является линейной системой, возбуждение происходит в плоскости, а узел стоячей волны представляет собой точечный объект. Далее будет рассматриваться размерность систем в соответствии с доминирующей протяжённостью. Если обозначить Nd — размерность движения системы, Nc — размерность системы, Nу — размерность узлов системы, то для струны получается
Для струны
Сухонос предполагает, что условие (1) выполняется для любых значений Nc. На рисунке 2 представлен случай двумерной (Nc = 2) среды в виде круглой плоской мембраны.
При колебаниях мембраны на её поверхности возникают линейные кольцевые структуры (размерность узлов Nу = 1), которые как бы маркируют те места на мембране, где не происходит никакого движения, представляя линейные «узлы» стоячих волн на плоскости. Можно увидеть, что для струны на рисунке 1 колебания происходят перпендикулярно линии струны, и для мембраны на рисунке 2 поперечные колебания также перпендикулярны, уже плоскости мембраны. На мембране могут быть стоячие волны вдоль радиуса в виде колец, а также можно предположить волны вдоль самих колец. Пространство возбуждения, в котором находятся кольцевые структуры пучностей колебаний, является трёхмерным,
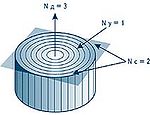
Перейдём теперь от двумерной среды к среде трёхмерной (Nc = 3). В этом случае размерность узлов равна двум (плоские перегородки объемных ячеек на рисунке 3), а пространство возбуждения должно быть четырёхмерным,
В своих ранних работах Сухонос проанализировал известную идею о том, что четвёртое пространственное измерение — это ортогональное трёхмерному пространству измерение. Он предположил, что вынужденные пульсации трёхмерного объёма (рис. 3), его периодическое сжатие-расширение должны приводить к трёхмерным стоячим волнам, узлы которых — суть перегородки у ячеек. Для подтверждения этого он рассматривает эксперимент, в котором кубический объём жидкости, насыщенный лёгкими частицами (взвесью), подвергается сжатию. Примером является остывающий жидкий сплав металла с различными примесями. По мере остывания объём отливки будет сжиматься со всех сторон, обеспечивая ортогональное к трёхмерному пространству сжатие. При этом сплав в процессе отвердения заполняется так называемыми зёрнами, двумерные границы между которыми образованы взвесью (добавками, порами и пр.). Эти границы и есть двумерные узлы четырёхмерных колебаний трёхмерной среды.
Если осуществить увеличение размерности среды до величины Nc = 4 и создать в ней определённое движение, ортогональное трёхмерному пространству, то в среде образуются узлы, размерность которых будет равна трём (Nу = Nс — 1 = 4 — 1 = 3). Сухонос предполагает, что такими узлами могут быть трёхмерные тела, устойчивость которых обуславливается лишь тем, что они являются узлами пятимерных колебаний в четырёхмерной среде. Данные трёхмерные узлы образуют устойчивый мир объектов Вселенной, которые есть сложные суперпозиции колебаний четырёхмерного пространства. Длительность существования систем Вселенной, их устойчивость к внешним воздействиям связана с мощностью узлов, то есть с энергетикой порождающих их колебаний. Отсюда следует, что описание всего многообразия жизни Вселенной можно осуществить с помощью теории волн и колебаний, но в среде более высокой размерности, чем до сих пор использовала традиционная наука.
Масштабное измерение как структурное свойство[править | править код]
Количество базовых измерений в физике определяется по числу степеней свободы или независимых величин, задающих местоположение физического тела или его элементов, рассматриваемых как точки, в заданной системе отсчёта. При этом количество измерений или степеней свободы задаёт размерность используемого пространства-времени. Добавляя масштабное измерение к четырёхмерному пространству-времени, мы получаем пятимерное многообразие, включающее в себя обычное пространство-время. Согласно порядку исторического осмысления это можно записать в виде (3+1+1)-пространства, где на первом месте отражены пространственные измерения, а затем измерения времени и масштаба. С точки зрения геометрии удобно считать оси всех измерений перпендикулярными друг другу.
По мнению Сергея Федосина, масштабное измерение является проявлением вложенности материи и следствием трансформации фундаментальных сил на разных уровнях материи. Масштабное измерение включает в себя четвёртое пространственное измерение (преобразование объёма бесконечного множества объектов за счёт изменения размеров приводит к новому подобному множеству), а также требует преобразования массы и скорости процессов (скорости течения времени) объектов, при перемещении наблюдателя от одного уровня на масштабной оси к другому уровню. Это вытекает из SPФ-симметрии, в соответствии с которой физические законы на разных уровнях материи остаются неизменными с точки зрения локального наблюдателя. В результате возникает масштабная инвариантность физических законов, а принцип общей ковариантности расширяется с учётом того, что на разных уровнях материи действуют разные по мощности поля гравитации. Кроме этого, относительность в масштабном измерении приводит к тому, что «правильные» физические уравнения необходимо должны иметь такую форму, чтобы масштабные преобразования оставляли их в силе на каждом уровне материи.
В четырёхмерном пространстве-времени простейшим четырёхмерным телом можно считать тело, состоящее из некоторого множества форм, которые принимает определённое трёхмерное тело за определённый период времени.
Моделью какого-либо четырёхмерного тела с учётом трёх пространственных измерений и масштабного измерения является множество трёхмерных тел, расположенных по определённому закону на масштабной оси. Эти трёхмерные тела должны изменять свои размеры в соответствующем интервале размеров, задающем размеры данного четырёхмерного тела. Разрез четырёхмерного тела в некоторой точке масштабной оси обнаруживает в сечении на месте разреза трёхмерное тело. Точнее говоря, в точке сечения должно быть объёмное изображение половины этого трёхмерного тела (чтобы увидеть остальную часть, тело необходимо развернуть и взглянуть на него с другой стороны). В месте сечения можно также представить проекцию трёхмерного изображения данной половины тела на одну сторону плоскости сечения. Аналогично моделью трёхмерного тела является дискретное или непрерывное множество тесно связанных друг с другом поверхностей, в совокупности дающих образ этого тела, а сечение тела даёт поверхность. Связь между трёхмерными телами в рассматриваемом четырёхмерном теле может быть задана посредством теории подобия (смотри подобие уровней материи). Разделение путём разрезов трёхмерного тела на части и разнесение этих частей в пространстве ещё не означает утраты трёхмерного тела, оно начинает существовать в новом виде и даже имеет возможность обратной сборки в исходное состояние. Четырёхмерное тело также можно мыслить в виде разнесённых отдельных трёхмерных тел, при разных конфигурациях которых или при сборке в тесное целое возникает та или иная четырёхмерная форма.
Возможен тривиальный случай, когда масштабная ось совмещается с одним из обычных трёх пространственных измерений. В этом случае мгновенный перенос трёхмерного тела вдоль оси такого пространственно-масштабного измерения даёт след в виде вырожденного четырёхмерного тела. Внешне это выглядит так, что трёхмерное тело становится непропорционально изменённым в некотором пространственном направлении, удлиняется, сжимается, перекашивается, изгибается, закручивается и т. д. В живописи существуют работы, отражающие подобные эксперименты с трёхмерным пространством. Масштабное изменение можно представить как сжатие трёхмерного тела в некотором направлении вплоть до превращения тела в плоскость, с последующим расширением в противоположном направлении до изомерной формы данного трёхмерного тела. Таким образом получается тело, вывернутое наизнанку, в котором левое заменяется на правое.
Введение времени увеличивает число измерений до пяти. В случае, если масштабное измерение рассматривается с учётом течения времени в объёме пространства, где находится некоторое трёхмерное, четырёхмерное или пятимерное тело, можно проследить изменение масштабных свойств (объёма, массы, состава вещества и других свойств тела) в зависимости от времени.
С физической точки зрения масштабное измерение не может свестись просто к пространственному пропорциональному изменению формы и объёма тел. Если имеется небольшая деревянная модель многоэтажного здания, то построенное в натуральную величину здание не сможет существовать, так как из-за своего веса оно раздавит нижние этажи. Причина этого в том, что с увеличением размера масса растёт пропорционально кубу этого размера, то есть гораздо быстрее. Отсюда следует, что подобные друг другу тела на разных уровнях материи не могут состоять из одного и того же вещества в том же самом состоянии. Свойства вещества должны быть такими, чтобы на каждом уровне материи обеспечивать существование объектов. Как правило, по мере увеличения размеров объектов при переходе с одного уровня материи на другой, происходит уменьшение плотности вещества объектов и характерной скорости движения этого вещества.[1] Последнее можно понимать как замедление времени подобных процессов. Например, чем больше по размерам объекты, тем больше времени занимает у них один оборот вокруг своей оси при вращении, дольше длятся другие типичные процессы. Относительное различие хода времени на масштабной оси позволяет наблюдать в некоторых процессах прошлое, настоящее и будущее одновременно. В частности, если на уровне атомов уже произошло разделение вещества на типичные частицы в виде нуклонов, то на уровне звёзд это ещё не наступило — большая часть звёзд находится на главной последовательности и ещё не превратились в нейтронные звёзды.
При движении вглубь материи обнаруживается обратная тенденция. Так, нуклоны на атомном уровне материи являются аналогами нейтронных звёзд на звёздном уровне материи, и средняя плотность вещества нуклонов превышает плотность вещества нейтронных звёзд (6,1∙ 1017 кг/м³ и 3,7∙ 1017 кг/м³ соответственно). Характерной скоростью для вещества нуклонов является скорость света
В соответствии с изменением физических параметров вещества на разных уровнях материи происходит также изменение действующих сил. Если на уровне планет и звёзд основной силой является гравитация, формирующая шаровидную форму тел и управляющая их движением друг возле друга, то на атомном уровне такую же роль играет сильная гравитация. При этом постоянная сильной гравитации на много порядков превышает обычную гравитационную постоянную.
Иерархия космических систем такова, что они группируются в отдельные масштабные уровни, расположенные приблизительно на одинаковом расстоянии друг от друга в логарифмической шкале размеров. Отсюда вытекает подобие уровней материи, когда между различными уровнями выводятся соотношения подобия не только по размерам, но и по массам, по скоростям протекания подобных процессов, по другим физическим параметрам. Следствием подобия являются звёздные постоянные, дискретность параметров звёзд, водородная система, квантованность параметров космических систем, гравитационная модель сильного взаимодействия, субстанциональные модели нейтрона, протона, электрона и фотона.
Благодаря вложенности одних уровней материи в другие массивные объекты состоят из частиц низших уровней материи. Это приводит к взаимосвязи характеристик объектов и состояний их вещества, а также к симметрии между свойствами частиц вещества и свойствами объектов, проявляющейся через отношения подобия. При этом обнаруживаются основные и промежуточные уровни материи. На основных уровнях материи достигают максимума действующие фундаментальные силы, то есть силы гравитации и электромагнитные силы. Одновременно растёт плотность вещества объектов, причём гравитационной силе притяжения противодействуют вначале электромагнитные силы, а затем сильное взаимодействие. Примерами здесь являются:
- Обычные звёзды главной последовательности, веществом которых является термически ионизованная плазма, давление которой противодействует гравитации.
- Белые карлики, в которых происходит вырождение плазмы, и гравитации противостоит фермиевское давление электронов.
- Нейтронные звёзды, состоящие из нейтронной жидкости, в которой согласно гравитационной модели сильного взаимодействия по мере сближения нейтронов увеличивается сила их отталкивания друг от друга за счёт полей кручения.
Роль слабого взаимодействия сводится к тому, что под действием фундаментальных сил и сильного взаимодействия в объектах после их образования происходит медленная трансформация их вещества. Например, нейтрон через очень большое по меркам атомных процессов время превращается в протон, электрон и нейтрино. Трансформация вещества может быть значительно ускорена под действием внешних факторов. Так, падающее на элементарную частицу нейтрино может быстро преобразовать вещество частицы и привести к её распаду на другие частицы.
Из описанного видно, что реализацию и проявление масштабного измерения в природе можно представить в виде бесконечной масштабной лестницы со ступеньками — уровнями материи, на которых расположены все известные объекты Вселенной. При этом подобные объекты на разных уровнях не являются простыми увеличенными или уменьшенными копиями друг друга, поскольку отличаются своим веществом и его свойствами, а также темпом течения своего времени. На высших ступеньках масштабной космической лестницы мы наблюдаем большие галактические системы и Метагалактику, за которыми должны располагаться ещё большие объекты. В нижней части обнаруживаются элементарные частицы, пока ещё гипотетические партоны и преоны, а также другие ещё более мелкие носители материи. В частности, частицам, из которых должны состоять нуклоны, присвоено название праоны.[10]
Масштабное измерение характеризует вложенность уровней материи как структурное свойство, задающее порядок расположения материальных объектов с учётом изменения их свойств. В отношении структуры имеется философский закон размножения структур, который формулируется следующим образом:
«Структуры, содержащиеся в сущности вещей и явлений и задающие их качество, обладают механизмами размножения, приводящими к поддержанию целостности этих структур и к их распространению через другие вещи и предметы.»
Другой философский закон описывает подобие носителей разных масштабных уровней материи:
«Распределение носителей по массе (по размерам, по другим связанным с массой параметрам) происходит по закону геометрической прогрессии, с выделением на каждой ступеньке характерных и доминирующих носителей, основных носителей и их спутников, причём между носителями на отдельных ступеньках и между целыми совокупностями ступенек наблюдаются соотношения подобия.»
Устойчивость масштабной лестницы материи как проявление структуры вложенных друг в друга уровней материи вытекает из самого способа образования новых материальных объектов, носит динамический характер и является следствием множественных взаимодействий частиц вещества и квантов поля. С одной стороны, разрозненные частички вещества стягиваются гравитационными силами и образуют плотное вещество новых массивных объектов. По мере роста массы объектов в них растёт внутреннее давление, увеличивается энергия движения частиц, что приводит к изменению состояния вещества. На основных уровнях материи возникает равновесие между притоком и оттоком массы на объекты. Это видно на примере массивных звёзд главной последовательности, которые за счёт высокой температуры излучают огромное количество энергии и теряют массу за счёт истечения вещества, компенсируя тем самым приток вещества извне. Для нейтронных звёзд также обнаружена небольшая вариация их массы, поскольку падающее на них вещество «разбрызгивается» в термоядерных вспышках. По-видимому, нейтронные звёзды, как звёздные аналоги нейтронов, и магнитары, как аналоги протонов, имеют максимальную плотность вещества, достигаемую в стабильных объектах под действием обычной гравитации (то же самое следует в отношении нуклонов и сильной гравитации).
С другой стороны, теория бесконечной вложенности материи предсказывает, что кванты гравитационного поля рождаются в основном в процессах, связанных с образованием и трансформацией вещества объектов на основных уровнях материи. Так, при образовании нейтронной звезды во вспышке сверхновой возникает мощное нейтринное излучение. Нейтронные звёзды и магнитары могут излучать джеты в виде потоков падающего на них вещества, являются источниками рентгеновского и гамма-излучения, а также и космических лучей. Это же справедливо и для нуклонов — они излучают нейтрино, потоки вещества и электромагнитного излучения. Все эти излучения могут входить в состав гравитонов, носителей гравитационного поля в теории гравитации Лесажа. Расчёты показывают, исходя из плотности энергии потоков гравитонов, что источником гравитонов для обычной гравитации являются излучения от частиц, находящихся на два или даже три основных уровня ниже, чем звёзды.[11] Гравитоны и заряженные частицы составляют основу электрогравитационного вакуума.
Таким образом, фундаментальные поля формируют объекты различных уровней материи, а эти объекты в свою очередь порождают кванты фундаментальных полей, действующие уже на более высоких масштабных уровнях материи. Что касается объектов промежуточных уровней материи, они образуются не только под действием фундаментальных сил, но и в процессах взаимодействия объектов друг с другом, либо с увеличением массы, либо с распадом на более мелкие составляющие. Так, при образовании планет Солнечной системы при многочисленных столкновениях произошло разделение между планетами, спутниками, астероидами, метеоритами, кометами, микрометеоритами и космической пылью, и эти объекты заняли определённые масштабные ниши по массам и размерам. Анализ этих ниш показывает, что объекты в них по массам и размерам соотносятся друг с другом в геометрической прогрессии, а переход между нишами осуществляется по закону перехода количества в качество.[12] В каждой нише могут быть выделены характерные основные носители, стандартные носители и граничные точки меры, в которых наступает неустойчивость объектов в существующих условиях.
Масштабное измерение описывает не только природные физические или химически связанные объекты, но пригодно и для описания живых существ. Оказывается, что живые существа и носители жизни точно повторяют основные особенности объектов разных уровней материи, поскольку располагаются на тех же уровнях материи в отношении своих размеров и масс.[13]
Как и другие носители материи, живые существа могут образовывать бесконечную вложенность уровней живого, так что в каждом организме существует множество уровней с соответствующими живыми носителями на этих уровнях. Живое вещество является сложным переплетением живого и неживого, причём живое явно управляет и доминирует над неживым. В свою очередь, в неживом также существует живое, но внешне не в проявленном, в слабом виде. Эволюция живого в масштабном измерении есть не только продвижение в пространстве и времени, но и трансформация самой структуры живого с тем, чтобы приспособиться к изменяющимся условиям существования на новых масштабных уровнях.
Применение[править | править код]
Исследованием масштабного измерения и принадлежащих ему объектов занимается теория бесконечной вложенности материи. Эта теория позиционирует себя как междисциплинарная системная наука и часть системологии, имеющая дело с космическими системами различных масштабов. Открытие масштабного измерения для научного исследования не просто раздвигает горизонты науки,[14] но и помогает находить неизвестные ранее закономерности в физике и математике.[15] Обнаружение прямых связей между микро, макро и мега-миром в нашей Вселенной позволяет понять её эволюцию как эволюцию иерархически вложенных уровней материи, уточнить картину мира,[16] включить в научное мировоззрение новые понятия и линии развития. С практической точки зрения построенные с помощью теории подобия субстанциональные модели элементарных частиц позволяют сделать существенные и необходимые дополнения в квантовой механике и в теории элементарных частиц, что может привести к полезным результатам как в физике, так и в технологиях. Одним из примеров прогресса в технике является создание модели двигателя космического корабля, черпающего энергию из космического вакуума. Идея двигателя основана на управлении частицами электрогравитационного вакуума с помощью электромагнитных полей. [17]
Новые перспективы открываются в биологии как в науке о жизни и живых существах. Живые существа можно понимать как активные открытые системы, обладающие благодаря бесконечной вложенности живых систем глубокими внутренними источниками упорядочения, диктующими поведение и обеспечивающие функционирование таких систем. При этом экспансия живого может происходить как в рамках одного уровня материи (расселение в необжитые территории), так и путём перехода на новые уровни материи. Последнее неизбежно требует перестройки форм существования живого, поскольку при большом увеличении размеров среды обитания возникают проблемы с целостностью всей системы в окружающих условиях и с замедлением процессов распределения ресурсов. Познание стратегии существования и эволюции живого достаточно важно и для развития человечества в целом.
В медицине наука подошла к тому, чтобы на генном уровне воспроизводить клоны живых организмов из единого генного материала и исправлять геном с целью излечения от некоторых заболеваний. Планируется также использовать генетические методы для защиты от опасных микроорганизмов и вирусов. Однако, как следует из теории бесконечной вложенности материи, должны существовать и такие живые существа, размеры которых много меньше прионов, мельчайших из известных на сегодняшний день частиц живого. В таком случае возможны заболевания, связанные с такими существами, и оказывающиеся за пределами возможностей современной медицины. Для изучения подобных живых частиц известные сейчас нанотехнологии должны быть заменены на ещё более мощные и глубокие методы исследований.
Ссылки[править | править код]
- ↑ Перейти обратно: а б Федосин С. Г. Физика и философия подобия от преонов до метагалактик, Пермь: Стиль-МГ, 1999, 544 стр. Табл.66, Ил.93, Библ. 377 назв. ISBN 5-8131-0012-1.
- ↑ Блаватская Е. П. «Тайная доктрина» («The Secret Doctrine», 1884—1891).
- ↑ Успенский П. Д. Tertium Organum. Ключ к загадкам мира. С.-Петербург, Андреев и сыновья, 1992, 242 с.
- ↑ Сухонос С. И. На пороге четырёхмерной цивилизации. – В альманахе «Логос Вселенной». Выпуск первый. – М. : Белые альвы, 1999, с.5-32.
- ↑ Fournier D’Albe, E. E. Two New Worlds: I The Infra World; II The Supra World, 1907, London: Longmans Green.
- ↑ Yun Pyo Jung. «Infinite Universe In A Mote», Sagyejul Publishing Co., 1994, 290 pages. Безграничная Вселенная в пылинке.
- ↑ Oldershaw R.L. Discrete Scale Relativity. Astrophysics and Space Science, 2007, Vol. 311, N. 4, P. 431‒433. DOI: 10.107/s10509‒007‒9557-x.
- ↑ Сухонос С. И. Структура устойчивых уровней организации материального мира. — СПб.: Гидрометеоиздат, 1992., а также Сухонос С. И. Масштабная гармония Вселенной. — М., София, 2000, 312 с.
- ↑ Сухонос С. Взгляд издали, ж-л «Знание-сила», 1981, № 9, с.31‒33.
- ↑ Федосин С. Г. Физические теории и бесконечная вложенность материи. Пермь, 2009, 844 стр., Табл. 21, Ил.41, Библ. 289 назв. ISBN 978-5-9901951-1-0.
- ↑ Комментарии к книге: Федосин С. Г. Физические теории и бесконечная вложенность материи. Пермь, 2009, 844 стр., Табл. 21, Ил.41, Библ. 289 назв. ISBN 978-5-9901951-1-0.
- ↑ Федосин С. Г. Основы синкретики. Философия носителей, М: Эдиториал УРСС, 2003, 464 стр., Табл.28, Ил.11, Библ. 102 назв. -Х.
- ↑ Федосин С. Г. Носители жизни: происхождение и эволюция. — С.-Петербург, Изд-во «Дмитрий Буланин», 2007, 104 с. ISBN 978-5-86007-556-6.
- ↑ Сухонос С. И. Фильм-лекция «Четвертое измерение». 15 февраля 2011.
- ↑ Fedosin S.G. Scale Dimension as the Fifth Dimension of Spacetime. Turkish Journal of Physics, Vol. 36, No 3, pp. 461‒464 (2012). http://dx.doi.org/10.3906/fiz-1110-20; статья на русском языке: Масштабное измерение как пятое измерение пространства-времени.
- ↑ The Scale of the Universe — Изображение масштабной оси с объектами на ней.
- ↑ Fedosin S.G. The Principle of Operation of an Engine That Draws Energy from the Electrogravitational Vacuum. Jordan Journal of Physics, Vol. 17, No. 1, pp. 87-95 (2024). https://doi.org/10.47011/17.1.8. // Принцип действия двигателя, черпающего энергию из электрогравитационного вакуума.