Неуловимой физической формуле 111 лет
Курьёзы истории или замысел Бога?.
Макс Карл Эрнст Людвиг Планк[править | править код]
Макс Планк (1858 — 1947) — немецкий физик-теоретик, основоположник квантовой физики. Лауреат Нобелевской премии по физике (1918)
Научные труды Планка посвящены термодинамике, теории теплового излучения, квантовой теории, специальной теории относительности, оптике. Он сформулировал второе начало термодинамики в виде принципа возрастания энтропии и использовал его для решения различных задач физической химии. Применив к проблеме равновесного теплового излучения методы электродинамики и термодинамики, Планк получил закон распределения энергии в спектре абсолютно чёрного тела (формула Планка) и обосновал этот закон, введя представление о квантах энергии и кванте действия. Это достижение положило начало развитию квантовой физики, разработкой различных аспектов которой он много занимался в последующие годы («вторая теория» Планка, проблема структуры фазового пространства, статистическая механика квантовых систем и так далее). Планк впервые вывел уравнения динамики релятивистской частицы и заложил основы релятивистской термодинамики. Ряд работ Планка посвящён историческим, методологическим и философским аспектам науки.
Основные даты[править | править код]
- 1858 - 23 апреля в Киле родился Макс Планк
- 1867 - Максимилиановская гимназия
- 1874 - студент Мюнхенского университета
- 1877 - студент Берлинского университета
- 1878 - право работать учителем физики и математики
- 1979 - Мюнхенский университет - степень доктора философии
- 1880 - работа «Состояния равновесия изотропных тел при различных температурах» - место приват-доцента
- 1885 - место экстраординарного профессора теоретической физики в Кильском университете
- 1886 - серия статей под общим названием «О принципе возрастания энтропии»
- 1887 - 1) Макс Планк женился на своей подруге детства Марии Мерк 2) книга «Принцип сохранения энергии»
- 1889 - экстраординарный профессор Берлинского университета
- 1891 - работа под общим названием «О принципе возрастания энтропии»
- 1892 - ординарная профессура по теоретической физике
- 1894 - действительный член Прусской академии наук
- 1895 - проблема теплового излучения
- 1900 - формула для распределения энергии в спектре абсолютно чёрного тела
- 1911 - первый Сольвеевский конгресс, посвящённый теме «Излучение и кванты»
- 1918 - Нобелевская премия по физике с формулировкой «в знак признания услуг, которые он оказал физике своим открытием квантов энергии»
- 1926 - покинул пост профессора Берлинского университета
- 1947 - 4 октября в Гёттингене скончался от инсульта
Планковские единицы[править | править код]
Пла́нковские едини́цы — система единиц измерения, одна из естественных систем единиц. Впервые предложена в 1899 году Максом Планком на основе скорости света , гравитационной постоянной и двух введенных им новых постоянных теории теплового излучения и (они отличаются от современных постоянных и на безразмерные множители). Первоначально планковские единицы были введены в докладе, сделанном 18 мая 1899 года на заседании Академии наук в Берлине и посвящённом обзору теории явлений теплового излучения, рассматриваемых с точки зрения электромагнитной теории света, и значению второго начала термодинамики в ней.
|
— Планк М. Избранные труды. М.: Наука, 1975. С. 232.
В 1900 году Макс Планк предложил новый закон излучения (закон Планка), в котором фигурировали две новые постоянные и . В 1906 году Планком была предложена система на основе постоянных , , и . Ныне под планковской системой понимается система единиц, в которой в качестве основных единиц выбраны следующие константы:
- — постоянная Дирака (постоянная Планка, делённая на );
- — скорость света (электродинамическая постоянная);
- — гравитационная постоянная;
- — постоянная Больцмана;
- — коэффициент пропорциональности в законе Кулона, где — электрическая постоянная.
Значения для первых четырёх констант, приведённых выше, рекомендованы CODATA.
Из основных планковских единиц выводятся все остальные единицы системы, например:
- Планковская масса килограмм.
- Планковская длина метров.
- Планковское время секунд.
- Планковская температура кельвинов.
- Планковский заряд кулонов, где — элементарный электрический заряд, — постоянная тонкой структуры, — постоянная Планка. Соответственно, постоянная тонкой структуры — это квадрат заряда электрона, выраженного в планковских зарядах.
- Планковская угловая частота 1,85487×1043 c−1.
Обычно, говоря о планковской системе, указывают, что в этом случае выполняется , и . Однако, в действительности, такая форма записи не точна. Она отражает лишь то, что соответствующая постоянная выбрана в качестве меры. Следует иметь в виду, что в планковской системе размерности отнюдь не исчезают, скорее, наоборот, они приобретают фундаментальный характер, поскольку составляются из фундаментальных постоянных.
Риторический вопрос[править | править код]
Кто запретил Максу Планку находить выражение для формулы силы (в естественной системе единиц)? или Как выглядит закон всемирного тяготения Ньютона в естественной системе единиц?
Альберт Эйнштейн[править | править код]
Альберт Эйнштейн (1879 — 1955) — физик-теоретик, один из основателей современной теоретической физики, лауреат Нобелевской премии по физике 1921 года.
Эйнштейн — автор более 300 научных работ по физике, а также около 150 книг и статей в области истории и философии науки, публицистики и др. Он разработал несколько значительных физических теорий:
- Специальная теория относительности (1905).
- Общая теория относительности (1907—1916).
- Квантовая теория фотоэффекта.
- Квантовая теория теплоёмкости.
- Квантовая статистика Бозе — Эйнштейна.
- Статистическая теория броуновского движения, заложившая основы теории флуктуаций.
- Теория индуцированного излучения.
- Теория рассеяния света на термодинамических флуктуациях в среде.
Он также предсказал «квантовую телепортацию», предсказал и измерил гиромагнитный эффект Эйнштейна — де Хааза. С 1933 года работал над проблемами космологии и единой теории поля. Активно выступал против войны, против применения ядерного оружия, за гуманизм, уважение прав человека, взаимопонимание между народами.
Эйнштейну принадлежит решающая роль в популяризации и введении в научный оборот новых физических концепций и теорий. В первую очередь это относится к пересмотру понимания физической сущности пространства и времени и к построению новой теории гравитации взамен ньютоновской. Эйнштейн также, вместе с Планком, заложил основы квантовой теории. Эти концепции, многократно подтверждённые экспериментами, образуют фундамент современной физики.
Основные даты[править | править код]
- 1879 - 14 марта в южно-германском городе Ульме родился Альберт Эйнштейн
- 1880 - семья переселилась в Мюнхен
- 1894 - Эйнштейны переехали из Мюнхена в итальянский город Павию
- 1895 - Альберт Эйнштейн прибыл в Швейцарию, чтобы сдать вступительные экзамены в Высшее техническое училище (Политехникум) в Цюрихе
- 1896 - он успешно сдал все выпускные экзамены в школе
- 1896 - был принят в Политехникум на педагогический факультет
- 1900 - Эйнштейн окончил Политехникум, получив диплом преподавателя математики и физики
- 1901 - Эйнштейн получил гражданство Швейцарии
- 1901 - берлинские «Анналы физики» опубликовали его первую статью «Следствия теории капиллярности»
- 1903 - он стал постоянным работником Федерального Бюро патентования изобретений
- 1905 — «Год чудес»: 1) «К электродинамике движущихся тел» 2) «Об одной эвристической точке зрения, касающейся возникновения и превращения света» 3) «О движении взвешенных в покоящейся жидкости частиц, требуемом молекулярно-кинетической теорией теплоты»
- 1907 - Эйнштейн опубликовал квантовую теорию теплоёмкости
- 1909 - должность экстраординарного профессора в Цюрихском университете
- 1911 - кафедра физики в пражском Немецком университете
- 1915 - уравнения поля общей теории относительности
- 1919 - отклонение света в поле тяготения Солнца
- 1922 - Нобелевская премия за теорию фотоэффекта (текст решения содержал нейтральное добавление: «… и за другие работы в области теоретической физики»)
- 1925 - статистика Бозе — Эйнштейна
- 1926 - квантовые проблемы и Единая теория поля
- 1933 - выезд в Соединённые Штаты Америки (Принстон, штат Нью-Джерси)
- До конца жизни Эйнштейн продолжал работу над исследованием проблем космологии, но главные усилия он направил на создание единой теории поля.
- 1955 - 18 апреля Альберт Эйнштейн умер в Принстоне от аневризмы аорты
Уравнения Эйнштейна[править | править код]
Уравнения Эйнштейна связывают между собой свойства материи, присутствующей в искривлённом пространстве-времени, с его кривизной. Они являются простейшими (наиболее линейными) среди всех мыслимых уравнений такого рода. Выглядят они следующим образом:
где — тензор Риччи, получающийся из тензора кривизны пространства-времени посредством свёртки его по паре индексов
— скалярная кривизна, свёрнутый с дважды контравариантным метрическим тензором тензор Риччи
— космологическая постоянная, представляет собой тензор энергии-импульса материи, — число пи, — скорость света в вакууме, — гравитационная постоянная Ньютона. Тензор называют тензором Эйнштейна, а величину — гравитационной постоянной Эйнштейна.
Здесь греческие индексы пробегают значения от 0 до 3. Дважды контравариантный метрический тензор задаётся соотношением
Тензор кривизны пространства-времени равен
где используются символы Кристоффеля, определяемые через производные от компонент дважды ковариантного метрического тензора
Символ Кристоффеля с одним верхним индексом по определению равен
Так как уравнения Эйнштейна не налагают никаких ограничений на используемые для описания пространства-времени координаты, то есть обладают свойством общей ковариантности, то они ограничивают выбор лишь 6 из 10 независимых компонент симметричного метрического тензора — система только из уравнений Эйнштейна недоопределена (математически это проявляется как автоматическое удовлетворение любым тензором Риччи четырём тождествам Бьянки). Поэтому их решение неоднозначно без введения некоторых ограничений на компоненты метрики, соответствующих однозначному заданию координат в рассматриваемой области пространства-времени и называемых поэтому обычно координатными условиями.
Решая уравнения Эйнштейна совместно с правильно подобранными координатными условиями, можно найти все 10 независимых компонент симметричного метрического тензора. Этот метрический тензор (метрика) описывает свойства пространства-времени в данной точке и используется для описания результатов физических экспериментов. Он позволяет задать квадрат интервала в искривлённом пространстве
который определяет «расстояние» в физическом (метрическом) пространстве. Символы Кристоффеля метрического тензора определяют геодезические линии, по которым объекты (пробные тела) двигаются по инерции. В наиболее простом случае пустого пространства (тензор энергии-импульса равен нулю) без лямбда члена одно из решений уравнений Эйнштейна описывается метрикой Минковского специальной теории относительности
Долгое время дискутировался вопрос о наличии в уравнениях Эйнштейна третьего члена в левой части. Космологическая постоянная Λ была введена Эйнштейном в 1917 году в работе «Вопросы космологии и общая теория относительности» для того, чтобы описать в ОТО статическую Вселенную, однако затем открытие расширения Вселенной разрушило философские и экспериментальные основания её учёта в теории гравитации. Данные современной количественной космологии, тем не менее, говорят в пользу модели Вселенной, расширяющейся с ускорением, то есть с положительной космологической постоянной (см. Модель ΛCDM). С другой стороны, величина этой постоянной настолько мала, что позволяет не учитывать её в любых физических расчётах, кроме связанных с астрофизикой и космологией в масштабах скоплений галактик и выше.
Уравнения Эйнштейна наиболее просты в том смысле, что кривизна и энергия-импульс в них входят лишь линейно, а кроме того, в левой части стоят все тензорные величины валентности 2, которые могут характеризовать пространство-время. Их можно вывести из принципа наименьшего действия для действия Эйнштейна — Гильберта:
где обозначения расшифрованы выше, представляет собой лагранжеву плотность материальных полей, а даёт инвариантный элемент 4-объёма пространства-времени. Здесь — определитель, составленный из элементов матрицы дважды ковариантного метрического тензора. Знак минус введён для того, чтобы показать, что определитель всегда отрицателен (для метрики Минковского он равен −1).
С математической точки зрения уравнения Эйнштейна являются системой нелинейных дифференциальных уравнений в частных производных относительно метрического тензора пространства-времени, поэтому сумма их решений не является новым решением. Приближённо линейность можно восстановить лишь при исследовании малых возмущений заданного пространства-времени, например, для слабых гравитационных полей, когда малы отклонения метрических коэффициентов от их значений для плоского пространства-времени и настолько же мала порождаемая ими кривизна.
Дополнительным обстоятельством, затрудняющим решение этих уравнений, является то, что источник (тензор энергии-импульса) подчиняется собственному набору уравнений — уравнениям движения той среды, что заполняет рассматриваемую область. Интерес представляет то обстоятельство, что уравнения движения, если их меньше четырёх, вытекают из уравнений Эйнштейна в силу локального закона сохранения энергии-импульса (см. далее). Это свойство известно как самосогласованность уравнений Эйнштейна и впервые было показано Д. Гильбертом в его знаменитой работе «Основания физики». Если же уравнений движения больше четырёх, то решать приходится систему из координатных условий, уравнений Эйнштейна и уравнений среды, что ещё более сложно. Именно поэтому такое значение придаётся известным точным решениям этих уравнений.
Важнейшие точные решения уравнений Эйнштейна включают: решение Шварцшильда (для пространства-времени, окружающего сферически симметричный незаряженный и невращающийся массивный объект), решение Райсснера — Нордстрёма (для заряженного сферически симметричного массивного объекта), решение Керра (для вращающегося массивного объекта), решение Керра — Ньюмена (для заряженного вращающегося массивного объекта), а также космологическое решение Фридмана (для Вселенной в целом) и точные гравитационно-волновые решения. Среди приближённых решений надо выделить приближённые гравитационно-волновые решения, решения для гравитационных возмущений на фоне космологического решения Фридмана — основу современной космологии, и решения, получаемые методами постньютоновского разложения. Численное решение уравнений Эйнштейна также представляет трудности, которые были решены только в 2000-х годах, что привело к появлению динамично развивающейся численной относительности.
Уравнения Эйнштейна без космологической постоянной были практически одновременно выведены в ноябре 1915 года Давидом Гильбертом (20 ноября, вывод из принципа наименьшего действия) и Альбертом Эйнштейном (25 ноября, вывод из принципа общей ковариантности уравнений гравитационного поля в сочетании с локальным сохранением энергии-импульса). Работа Гильберта была опубликована позднее, чем эйнштейновская (1916). По вопросам приоритета существуют разные мнения, освещённые в статье об Эйнштейне, и более полно в «Вопросы приоритета в теории относительности», однако сам Гильберт никогда на приоритет не претендовал и считал ОТО созданием Эйнштейна.
Риторический вопрос[править | править код]
Смог ли Альберт Эйнштейн найти выражение для силы взаимодействия двух электрических зарядов в естественной системе единиц? или Как выглядит закон взаимодействия электрических зарядов - закон Кулона (электростатика) - в естественной системе единиц?
—— "страусиноподобная" запись уравнения гравиполя без -члена.
Страус:
- голова -
- крылья - тензоры и
- тело - или
Приведение к нормальному виду:
или
.
Некоторые современные физики-теоретики метров и секунд считают за фундаментальные кванты пространства и времени. Поэтому можно называть квантово-классическим уравнением ГП Эйнштейна-Планка.
Для решения этого тензорного уравнения необходимо : а) ввести в физику и математику квантование пространства и времени; б) возможно, время - 5-мерно.
Суммируя записи по Планку и Эйнштейну (см. выше), возникает вопрос: «Осуществилась ли мечта А. Эйнштейна о создании Единой теории поля (гравитационное поле + электромагнитное поле)»?
А. Эйнштейн, кажется, так говорил (писал):«Из c и G нельзя ничего построить». За неимением под рукой его трудов, прошу найти это его высказывание. Буду заранее благодарен автору, который отыщет это и включит в эту статью.
Георгий Антонович Гамов[править | править код]
Георгий Антонович Гамов (1904 — 1968) — советский и американский физик-теоретик, астрофизик и популяризатор науки. Премия Калинги (1956).
Гамов известен своими работами по квантовой механике, атомной и ядерной физике, астрофизике, космологии, биологии. Он является автором первой количественной теории альфа-распада, одним из основоположников теории «горячей Вселенной» и одним из пионеров применения ядерной физики к вопросам эволюции звёзд. Он впервые чётко сформулировал проблему генетического кода. Широкую известность Гамову принесли его научно-популярные произведения, в которых живым и доступным языком рассказывается о современных научных представлениях.
Основные даты[править | править код]
- 1904 - 4 марта родился в Одессе Георгий Гамов
- 1921 - поступил на математическое отделение физико-математического факультета Новороссийского (Одесского) университета
- 1922 - Гамов решил поступить на физико-математический факультет Петроградского университета
- 1924 - Гамов был приглашён Дмитрием Рождественским в Государственный оптический институт
- 1926 - аспирантура
- 1928 - в Журнале Русского физико-химического общества статья «Мировые постоянные и предельный переход» - Гамов, Иваненко и Ландау
- 1928 - стажировка в Гёттинген
- 1932 - член-корреспондент в АН СССР
- 1934 - должность профессора в столичном Университете Джорджа Вашингтона
- 1936 - обобщение теории бета-распада Ферми
- 1938 - исключён из числа членов-корреспондентов АН СССР
- 1937—1940 - первая последовательная теория эволюции звёзд с термоядерным источником энергии
- 1940—1941 - роль нейтрино в катастрофических процессах, происходящих при вспышках новых и сверхновых звёзд
- 1942 - совместно с Теллером предложил теорию строения красных гигантов
- 1946 - Гамов активно включился в работу в области космологии, предложив модель «горячей Вселенной» (уточнение теории «Большого Взрыва»)
- 1948 - Гамов совместно с Ральфом Альфером и Робертом Херманом разработал теорию образования химических элементов путём последовательного нейтронного захвата (нуклеосинтез)
- 1954 - проблема генетического кода
- 1956 - Гамов получил от ЮНЕСКО премию Калинга за популяризацию науки
- 1968 - 19 августа Гамов умер в Боулдере
От Гамова до наших дней[править | править код]
Возрождение горячей модели имело место в совершенно ином контексте, нежели ее рождение. Новые измерения параметра Хаббла показали, что возраст Вселенной никак не меньше десяти миллиардов лет, и это сняло критическое расхождение между космологией и астрофизикой. Физика микромира претерпела радикальные изменения благодаря появлению теории кварков и разработке Стандартной модели элементарных частиц. Получила ряд подтверждений концепция темной материи, которая в середине 1950-х была чисто теоретической гипотезой. Наука о Вселенной (что произошло уже несколько позднее) обогатилась инфляционной космологией и открытием темной энергии. Были разработаны чрезвычайно эффективные методы математического моделирования космологических процессов, основанные на использовании мощных компьютеров. Last but not least, изменился коллективный менталитет астрономического сообщества, которое стало с куда большей готовностью рассматривать нестационарные процессы.
Наверное, стоит сравнить выводы Гамова и его партнеров по исследованиям с современной картиной раннего этапа эволюции Вселенной (оговорка: ни в коем случае не претендуя ни на полноту, ни на учет всех деталей — для этого просто нет места).
В последние годы астрофизики и космологи пришли к единой точке зрения относительно того, что происходило в нашей Вселенной, когда ее возраст перешел за одну микросекунду — более ранние события всё еще служат предметом дискуссий (напомню, что Альфер, Фоллин и Герман начали отсчет со ста микросекунд). В это время случилась так называемая Великая аннигиляция тогда еще свободных кварковых частиц, которая уничтожила все антикварки, однако пощадила возникший до этого мизерный избыток кварков. Когда возраст мироздания достиг 10 микросекунд, кварки потеряли независимость и слились в тройки и пары. Первый процесс породил частицы семейства барионов — протоны и нейтроны, — которые в будущем стали кирпичиками для построения атомных ядер. Попарное слияние привело к появлению крайне нестабильных частиц из семейства мезонов — в основном, пионов. На каждый барион приходилось около миллиарда высокоэнергетичных фотонов, температура которых в те времена составляла порядка 4 триллионов градусов.
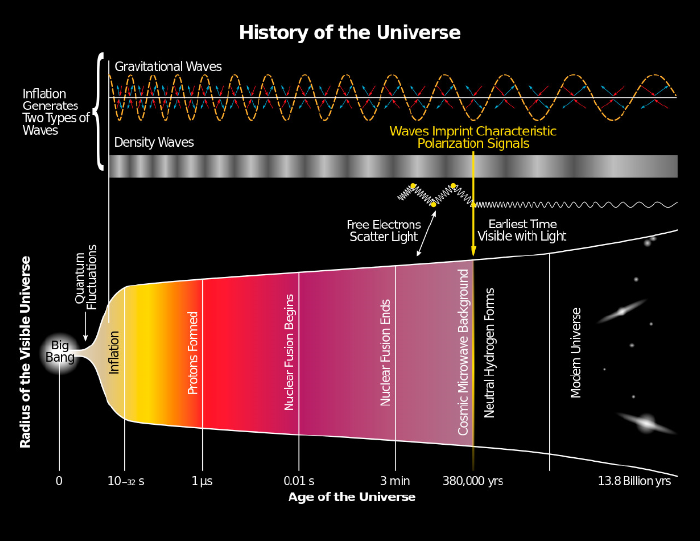
К концу первой секунды Вселенная заполнилась сверхгорячей плазмой, причем основной вклад в ее энергию вносили не барионы и не фотоны, а высокоэнергетичные лептоны, прежде всего электроны и позитроны. Они существовали в столь же ничтожном дисбалансе, что кварки и антикварки, однако всё же не аннигилировали полностью, поскольку из-за высокой температуры гамма-кванты порождали всё новые и новые электрон-позитронные пары. Эту фазу ранней истории Вселенной называют лептонной эрой (а предшествующую ей — адронной). Следует отметить, что диаметр ныне доступной для наблюдений части Вселенной тогда был меньше сотни астрономических единиц, то есть сильно уступал размерам современной Солнечной системы.
Лептонная эра продолжалась до тех пор, пока гамма-квантам хватало энергии для порождения электронов и позитронов. Кванту легче всего претерпеть подобное превращение в процессе рассеяния на протоне, поскольку в этом случае его минимальная энергия должна быть порядка суммарной энергии электрона и позитрона, то есть несколько превышать миллион электронвольт (для рассеяния на электроне или позитроне пороговая энергия вдвое больше). 1 МэВ соответствует средней температуре излучения порядка 11,6 миллиардов градусов. Из-за расширения Вселенной температура фотонного газа постоянно снижалась и достигла этой величины, когда возраст Мироздания составлял примерно одну секунду. Однако образование пар (всё в меньшем и меньшем количестве) продолжалось и позднее за счет горячего хвоста фотонного спектра, и только спустя несколько секунд, когда температура фотонов спустилась ниже 4 миллиардов градусов, оно полностью прекратилось. К моменту, когда Вселенной исполнилось 10 секунд, лептонная эра ушла в прошлое. Подобно кварковой эре, она оставила после себя очень горячую плазму, чья плотность энергии почти полностью обеспечивалась фотонами. Началась новая эра — радиационная.
В преддверии радиационной эры материя Вселенной претерпела еще одно серьезное превращение. Помимо ранее названных частиц в наследство от кварковой эры достались нейтрино — по одному на каждый фотон. Пока материя оставалась достаточно плотной и горячей, нейтрино интенсивно взаимодействовали с протонами и нейтронами, заставляя их превращаться друг в друга в процессах, аналогичных бета-распаду атомных ядер. В течение второй секунды Вселенная настолько расширилась, что нейтрино перестали рассеиваться на барионах и ушли в свободный полет. С этого момента космическое пространство стало прозрачным для нейтрино и остается таковым до сих пор.
Распаривание нейтрино и барионов оставило после себя неодинаковые количества протонов и нейтронов. Поскольку нейтроны превосходят протоны по массе, они рождались с меньшей вероятностью. Поэтому после полного выхода нейтрино из игры протоны преобладали над нейтронами примерно в отношении 6:1. Теперь вспомним, что протоны стабильны, тогда как время жизни свободного нейтрона в среднем составляет четверть часа. Когда возраст Вселенной дошел до 3 минут, 13% нейтронов распалось, и на каждый нейтрон стало приходиться по 7 протонов. Количество фотонов в расчете на один протон стабилизировалось на уровне 1,6 миллиарда и с тех пор почти не изменилось.
В истории Мироздания трехминутная отметка очень важна. Именно на этой стадии впервые появилась возможность формирования самых простых составных ядер — ядер дейтерия. Энергия связи такого ядра равна 2,2 МэВ, что соответствует температуре порядка 25 миллиардов градусов. Температура первичной плазмы упала до этой величины, когда Вселенной было всего 1/4 секунды. Можно подумать, что дейтерий начал образовываться уже тогда, но такой вывод будет ошибочным. Электромагнитное излучение Вселенной еще долго содержало достаточно горячих фотонов, которые разбивали новорожденные ядра дейтерия. Дейтерий смог выжить, лишь когда доля фотонов с энергией более 2,2 МэВ сократилась до одной миллиардной (вспомним, что общее число фотонов в полтора миллиарда раз превышало число подлежащих объединению барионов!). Это случилось, когда возраст Вселенной достиг одной минуты, а еще через две минуты процесс синтеза дейтерия пошел в полную силу. Новорожденные ядра этого изотопа стали участниками различных ядерных реакций, в результате которых появились альфа-частицы — ядра гелия. Этот процесс занял всего несколько минут и задействовал практически все нейтроны (очень небольшая их часть пошла на непереработанные в гелиевом синтезе ядра дейтерия, трития, гелия-3, лития и бериллия). Поскольку исходное соотношение чисел протонов и нейтронов равнялось 7:1, каждая новая альфа-частица оставляла после себя 12 свободных протонов. Так космическое пространство оказалось заполненным ядрами водорода ( 75% общей массы) и гелия ( 25%). В наше время эти показатели равны 74% и 24% — оставшиеся 2% приходятся на более тяжелые элементы, порожденные процессами звездного нуклеосинтеза.
При синтезе гелия выделяется изрядная энергия (иначе не зажигались бы звезды и не взрывались водородные бомбы). Всего за несколько минут во вселенской термоядерной печи сгорело в 100 раз больше водорода, чем потом во всех звездах нашей Вселенной. Однако при этом ничего особенного не произошло. Вселенная лишь немного нагрелась, после чего продолжала остывать в ходе дальнейшего расширения. Поскольку потепление охватило весь объем космоса, оно не породило компактных областей горячего сжатого газа в более холодной и разреженной среде, которые возникают при детонации любого заряда, хоть химического, хоть атомного. Таким образом, гигантское выделение энергии в ходе первичного нуклеосинтеза практически не сказалось на эволюции Вселенной (к слову, это же можно сказать и о двух еще более сильных прогревах Космоса во время аннигиляции кварков и антикварков, а затем электронов и позитронов).
Пойдем дальше. Первичный нуклеосинтез вновь преобразовал состав горячей плазмы юной Вселенной. А вот потом в течение 380 тысяч лет она не претерпевала никаких качественных превращений — правда, за одним исключением. Когда Вселенной стукнуло 57 тысяч лет, плотность лучевой энергии (к ней относят и энергию реликтовых нейтрино) сравнялась с плотностью энергии частиц, а потом начала от нее отставать. Это и стало концом радиационной эры.
Каким тогда казался бы Космос разумному наблюдателю, если бы таковой существовал? Когда Вселенной стукнуло 50 тысяч лет, она впервые засветилась видимым для нас голубым светом (до этого реликтовые фотоны были ультрафиолетовыми, а еще раньше, когда возраст Вселенной двигался от полутора минут к 600 годам — рентгеновскими). К двухсоттысячелетней возрастной отметке цвет фотонного фона сместился от голубого к желтому, еще через 200 тысяч лет стал оранжевым, а по достижении миллиона лет сделался темно-красным. В возрасте 5 миллионов лет температура Вселенной упала до 600 кельвинов, практически все реликтовые фотоны перешли в инфракрасную зону, и в космическом пространстве настала беспросветная тьма. Она начала рассеиваться лишь после появления самых первых звезд.
Но что же все-таки произошло через 380 тысяч лет после Большого взрыва? Несколькими десятками тысяч лет ранее электроны начали объединяться с ядрами. Сначала альфа-частицы присоединяли к себе по единственному электрону и превращались в однократно ионизированные атомы гелия, а затем и по второму, так что в итоге получались нейтральные атомы этого элемента. Позднее то же самое случилось и с протонами, которые положили начало атомам водорода. Подобные слияния стали возможными потому, что в лучевом фоне сократилось количество фотонов с энергией больше энергии ионизации атомов гелия и водорода. Этот процесс так называемой рекомбинации растянулся на 80 тысяч лет и практически завершился, когда температура фотонного фона упала ниже 3000 кельвинов. В общем, повторилась трансформация, имевшая место в односекундной Вселенной. Тогда пространство стало прозрачным для нейтрино, а теперь — для квантов электромагнитного излучения. Стоит отметить, что некоторые авторы считают концом радиационной эры именно рекомбинацию — но это уже вопрос вкуса.
Рекомбинация стала важнейшей вехой в истории фотонного газа. Остывшие кванты электромагнитного излучения уже не могли рассеиваться на нейтральных атомах и, как некогда нейтрино, отправились в путешествие по космосу. Именно эти реликтовые фотоны, остывшие с тех пор до 2,725 кельвинов, мы называем фоновым микроволновым излучением. Хочу подчеркнуть, что в основополагающей работе Альфера и Германа о рекомбинации ровно ничего не сказано. Этот процесс распаривания электромагнитного излучения и вещества был понят гораздо позднее (P. J. E. Peebles, 1968. Recombination of the Primeval Plasma; Я. Б. Зельдович, В. Г. Курт, Р. А. Сюняев, 1968. Рекомбинация водорода в горячей модели Вселенной).
И что же получилось в итоге? В космическом пространстве не стало свободных заряженных частиц, следовательно, исчезла плазма! В той или иной форме она существовала как минимум с микросекундного возраста Вселенной, а в результате рекомбинации на многие миллионы лет уступила место электрически нейтральному водородно-гелиевому газу, соседствующему (и взаимодействующему посредством гравитации!) со столь же нейтральными частицами темной материи. Когда Вселенная состарилась до 100 миллионов лет, а температура фонового излучения опустилась до 80 кельвинов, темная материя начала стягиваться за счет собственного тяготения во всё более и более плотные сгустки. Еще через 100 миллионов лет эти сгустки стали втягивать в себя частицы космического газа, из которых сформировались коллапсирующие облака, положившие начало первым звездам (стоит отметить, что эти даты представляют из себя верхнюю границу начала эры рождения звезд — по другим моделям, они начали вспыхивать уже через 50–100 миллионов лет после Большого взрыва).
Как бы то ни было, уже предшественники первого поколения этих светил (его называют звездами популяции III), протозвезды, начали возрождать плазменное состояние материи, которое сейчас доминирует в космосе. Постепенно всё большая доля космического водорода переходила в ионизированное состояние из-за поглощения звездного света, и космическое пространство всё больше заполнялось протонами и электронами. Этот процесс дал ощутимые результаты примерно через полмиллиарда лет после начала процесса звездообразования. Так началась эпоха реионизации, которая к концу первого миллиарда лет существования Вселенной завершилась полной ионизацией межгалактического водорода. Некогда исчезнувшая плазма возродилась в новом качестве. Пожалуй, на этом можно и остановиться.
- Текст Алексея Левина
Риторический вопрос[править | править код]
Смог ли Джордж (Георг) Гамов найти выражение для магнитной силы - силы Лоренца - в естественной системе единиц? или Как выглядит 2-ой закон динамики Ньютона в естественной системе единиц?
.
.
.
.
.
Тест на интеллект современников (2016): 12.05 — 31.12[править | править код]