Цветовые координаты (версия Миг)

Цветовые координаты — количественное описание цветового воздействия в трехмерной системе координат, например (L*, a*, b*) или (X, Y, Z), полностью определяющие цвет (версия Миг) любой точки цветовой модели, при соблюдении некоторых стандартизованных условий рассматривания цвета.

Введение

Трехмерное представление цветового пространства человека

Рисунок Аддитивного синтеза цвета основных цветов RGB

Основой математического описания цвета в колориметрии является экспериментально установленный факт, что любой цвет при соблюдении упомянутых условий можно представить в виде смеси (суммы) определённых количеств 3 линейно независимых цветов, т. е. таких цветов, каждый из которых не может быть представлен в виде суммы каких-либо количеств 2 других цветов. Групп (систем) линейно независимых цветов существует бесконечно много, но в колориметрии используются лишь некоторые из них. Три выбранных линейно независимых цвета RGB называют основными цветами; они определяют цветовую координатную систему — ЦКС. При этом 3 числа, описывающие данный цвет (RGB), являются количествами основных цветов в смеси, цвет которой зрительно неотличим от данного цвета; это и есть цветовые координаты — ЦК данного цвета.

Экспериментальные результаты, которые закладывают в основу разработки колориметрической ЦКС, получают при усреднении данных наблюдений (в строго определённых условиях) большим числом наблюдателей; поэтому они не отражают точно свойств цветового зрения какого-либо конкретного наблюдателя, а относятся к т. н. среднему стандартному колориметрическому наблюдателю.

Смысл цветовых координат

Будучи отнесены к стандартному наблюдателю в определённых неизменных условиях, стандартные данные смешения цветов и построенные на них колориметрической ЦКС описывают фактически лишь физический аспект цвета, не учитывая изменения цветовосприятия глаза при изменении условий наблюдения и по др. причинам.

Когда ЦК какого-либо цвета откладывают по 3 взаимно перпендикулярным координатным осям, этот цвет S,M,L (см. рис.К) геометрически представляется точкой в трёхмерном, т. н. цветовом, пространстве или же вектором, начало которого совпадает с началом координат, а конец — с упомянутой точкой цвета (см. рис.4). Точечная и векторная геометрическая трактовки цвета равноценны и обе используются при описании цветов. Точки, представляющие все реальные цвета, заполняют некоторую область цветового пространства. Но математически все точки пространства равноправны, поэтому можно условно считать, что и точки вне области реальных цветов представляют некоторые цвета. Такое расширение толкования цвета как математического объекта приводит к понятию т. н. нереальных цветов, которые невозможно как-либо реализовать практически. Тем не менее с этими цветами можно производить математические операции так же, как и с реальными цветами, что оказывается чрезвычайно удобным в колориметрии. Соотношение между основными цветами RGB в ЦКС (цветовая координатная система) выбирают так, что их количества, дающие в смеси некоторый исходный цвет (чаще всего белый), принимают равными 1.

Субъективно «качество» цвета, не зависящее от абсолютной величины цветового вектора и называемое его цветностью, геометрически удобно характеризовать в двумерном пространстве — на «единичной» плоскости цветового пространства, проходящей через 3 единичные точки координатных осей (осей основных цветов). Линии пересечения единичной плоскости с координатными плоскостями образуют на ней равносторонний треугольник, в вершинах которого находятся единичные значения основных цветов. Этот треугольник часто называют треугольником Максвелла. Цветность какого-либо цвета определяется не 3 его ЦК, а соотношением между ними, т. е. положением в цветовом пространстве прямой, проведённой из начала координат через точку данного цвета. Другими словами, цветность определяется только направлением, а не абсолютной величиной цветового вектора и, следовательно, её можно характеризовать положением точки пересечения этого вектора (либо указанной прямой) с единичной плоскостью. Вместо треугольника Максвелла часто используют цветовой треугольник более удобной формы — прямоугольный и равнобедренный. Положение точки цветности в нём определяется двумя координатами цветности, каждая из которых равна частному от деления одной из ЦК на сумму всех 3 ЦК. Двух координат цветности достаточно, т.к. по определению сумма её 3 координат равна 1. Точка цветности исходного (опорного) цвета, для которой 3 цветовые координаты равны между собой (каждая равна 1/3), находится в центре тяжести цветового треугольника. (См. также )

Принцип построения цветовой модели

Рис. 4. Единичная плоскость и нейтральный цвет N (Например, белый при равных значениях 0,333 основных цветов RGB, что в сумме = 1) в трёх-координатном цветовом пространстве, что даёт белую точку

Свойства цветового зрения учитываются в колориметрии по результатам экспериментов со смешением цветов. В таких экспериментах выполняется зрительное уравнивание чистых спектральных цветов (т. е. цветов, соответствующих монохроматическому свету с различными длинами волн) со смесями 3 основных цветов. Оба цвета наблюдают рядом на 2 половинках фотометрического поля сравнения. По достижении уравнивания измеряются количества 3 основных цветов и их отношения к принимаемым за 1 количествам основных цветов в смеси, уравнивающей выбранный опорный белый цвет. Полученные величины будут ЦК уравниваемого цвета в ЦКС, определяемой основными цветами прибора и выбранным опорным белым цветом. Если единичные количества красного, зелёного и синего основных цветов обозначить как для (RGB): (R), (G), (B), а их количества в смеси (RGB): ЦК — R, G, B, (cм. рис.4), то результат уравнивания можно записать в виде цветового уравнения: (RGB) — Ц* = R (R) + G (G) + S (S). Легко заметить, что это линейное уравнеие. Описанная процедура не позволяет уравнять большинство чистых спектральных цветов со смесями 3 основных цветов прибора. В таких случаях некоторое количество одного из основных цветов (или даже двух) добавляют к уравниваемому цвету. Цвет получаемой смеси уравнивают со смесью оставшихся 2 основных цветов прибора (или с одним). В цветовом уравнении это учитывают переносом соответствующего члена из левой части в правую. Так, если в поле измеряемого цвета был добавлен красный цвет, то Ц* = — R(R), G(G), B(B). При допущении отрицательных значений ЦК уже все спектральные цвета можно выразить через выбранную тройку основных цветов. При усреднении результатов подобной процедуры для нескольких наблюдателей были получены значения количеств 3 определённых цветов, требующиеся в смесях, зрительно неотличимых от чистых спектральных цветов, которые соответствуют монохроматическим излучениям одинаковой интенсивности. При графическом построении зависимостей количеств основных цветов от длины волны получаются функции длины волны, называемые кривыми сложения цветов или просто кривыми сложения.

Кривые сложения цветов

Рис. 1. Кривые сложения для ЦКС МКО RGB.

Рис. 2. Кривые сложения для ЦКС МКО XYZ.

Рис. 3. График цветностей для системы XYZ и цветовой треугольник системы RGB (R — красный, G — зелёный, B — синий).

Кривые сложения цветов играют в колориметрии большую роль. По ним можно рассчитать количества основных цветов, требуемые для получения смеси, зрительно неотличимой от цвета излучения сложного спектрального состава, т. е. ЦК такого цвета в ЦКС, определяемой данными кривыми сложения. Для этого цвет сложного излучения представляют в виде суммы чистых спектральных цветов, соответствующих его монохроматическим составляющим (с учётом их интенсивности). Возможность подобного представления основана на одном из опытно установленных законов смешения цветов, согласно которому ЦК цвета смеси равны суммам соответствующих координат смешиваемых цветов. Таким образом, предполагают, что кривые сложения должны характеризовать реакции на излучение 3 разных приёмников излучения. Однако функции спектральной чувствительности 3-х типов пригментов обнаруженных в сетчатке глаза человека, описывают кривые сложения в физиологической ЦКС. С точки зрения теории трёхкомпонентного цветного зрения, каждой из бесконечно большого числа возможных ЦКС должна соответствовать своя группа из 3 кривых сложения, причём все группы кривых сложения должны быть связаны между собой линейными соотношениями. Следовательно, кривые сложения любой из всех возможных ЦКС можно считать линейными комбинациями функций спектральной чувствительности 3-х типов приёмников человеческого глаза — колбочек. (Cм. Математика цветного зрения (версия Миг))

Фактически основой всех ЦКС является система, кривые сложения которой были определены экспериментально. Её основными цветами являются чистые спектральные цвета, соответствующие монохроматическим излучениям с длинами волн 700,0 нм (красный), 546,1 нм (зелёный) и 435,8 нм (синий). Исходная (опорная) цветность — цветность равноэнергетического белого цвета Е (т. е. цвета излучения с равномерным распределением интенсивности по всему видимому спектру). Кривые сложения этой системы, принятой Международной комиссией по освещению (МКО) в 1931 и известной под название международной колориметрической системы МКО RGB (от англ., red — красный, green — зелёный, blue — синий), показаны на рис. 1. (См. Цветовое пространство CIE 1931).

Кривые сложения системы МКО RGB имеют отрицательные участки (отрицательные количества основных цветов) для некоторых спектральных цветов, что неудобно при расчётах. Наряду с системой RGB МКО в 1931 приняла другую ЦКС, систему XYZ (версия Миг), в которой отсутствовали недостатки системы RGB и которая дала ряд др. возможностей упрощения расчётов. Основными цветами (X), (Y), (Z) системы XYZ являются нереальные цвета (т. е. допускается существование несуществующих цветов!), выбранные так, что кривые сложения этой системы (рис. 2) не имеют отрицательных участков, а координата Y равна яркости (См. Яркость) наблюдаемого окрашенного объекта, т.к. кривая сложения у совпадает с функцией относительной спектральной световой эффективности (См. Спектральная световая эффективность) стандартного наблюдателя МКО для дневного зрения. На рис. 3 показан график цветностей (цветовой треугольник) х, у системы XYZ. На нём приведены линия спектральных цветностей, линия пурпурных цветностей, цветовой треугольник (R) (G) (В) системы МКО RGB, линия цветностей излучения абсолютно чёрного тела и точки цветностей стандартных источников освещения МКО А, В, С и D. Цветность равноэнергетического белого цвета Е (опорная цветность системы XYZ) находится в центре тяжести цветового треугольника системы XYZ. Эта система получила всеобщее распространение и широко используется в колориметрии. Но (в связи с принятыми допущениями) она естественно не отражает цветоразличительных свойств глаза, т. е. одинаковые расстояния на графике цветностей х, у в различных его частях не соответствуют одинаковому зрительному различию между соответствующими цветами при одинаковой яркости.

Создать полностью зрительно однородное цветовое пространство таким методом до сих пор не удаётся. Это связано с неспособностью взятой за основу трёхкомпонентной теории цветовосприятия описать, на основе экспериментально полученных спектров чувствительности фотопигментов, механизма цветовосприятия. Поэтому предложено много различных эмпирических формул для подсчёта числа цветовых различий (порогов цветоразличения) между разными цветами. Более ограниченная задача — создание зрительно однородного графика цветностей — приблизительно решена. МКО в 1960 рекомендовала такой график u, v, полученный в 1937 Д. Л. Мак-Адамом путём видоизменения графика, предложенного Д. Б. Джаддом (оба — США) на основании многочисленных экспериментальных данных. Для подсчёта числа порогов цветоразличения ΔE между разными цветами с 1970 годов (по временной рекомендации МКО) используется эмпирическая формула Г. Вышецкого:

$ΔE=\sqrt{(U_{\rm 1}-U_{\rm 2})^2 + (V_{\rm 1}-V_{\rm 2})^2 + (W_{\rm 1}-W_{\rm 2})^2}$

где:

$W = 25Y^1/_3 — 17$,

$U = 13W (u — u_0)$,

$V = 13W (v — v_0)$.

Здесь:

$u_0, v_0$ — цветность опорного белого цвета,

$Y$ — коэффициент отражения в данной точке объекта в %.

Описание, приведённое выше, показывает, что цель процесса измерения цвета — определение его ЦК в некоторой ЦКС. Чаще всего это — стандартная колориметрическая система МКО XYZ.

Нахождение цветовых координат

Когда цвет (при объективных цветовых измерениях (Ц. и.) всегда имеется в виду цвет окрашенного предмета или источника света (cм. Источники света)) представлен спектральным распределением плотности, мощности — дисперсии излучения (испускаемого источником, либо отражённого или пропущенного предметом), то для нахождения его ЦК нужно использовать кривые сложения в качестве взвешивающих функций, оценивающие это излучение. Такая оценка может выполняться двумя путями.

Спектрофотометрический метод цветного измерения

Первый путь (спектрофотометрический метод цветового источника) состоит в измерении энергии спектрального распределения плотномти, мощности — дисперсии излучения с последующим расчётом ЦК при перемножении найденной функции спектрального распределения на 3 функции сложения и интегрирования произведений. Если Е (λ) — функция спектрального распределения источника, ρ(λ) — функция спектрального отражения или пропускания предмета — X, Y, Z определяются следующим образом: $$X= \int_{380}^{780} I(\lambda)\,\overline{x}(\lambda)\,d\lambda$$ $$Y= \int_{380}^{780} I(\lambda)\,\overline{y}(\lambda)\,d\lambda$$ $$Z= \int_{380}^{780} I(\lambda)\,\overline{z}(\lambda)\,d\lambda$$

(интегрирование проводится в диапазоне длин волн видимого излучения — от 380 до 780 нм).

Практически интегрирование заменяют суммированием через интервал Δλ (от 5 до 10 нм), т.к. подынтегральные спектральные функции обычно неудобны для интегрирования:

Спектральное распределение излучения и спектральную характеристику отражения (пропускания) измеряют, диспегируя свет в спектр (версия Миг), например, в Спектрофотометре или Монохроматоре. Кривые сложения задаются в виде таблиц значений удельных координат через 5 или 10 нм. Имеются также таблицы величин Е (λ) и т.д. для стандартных источников света МКО А, В, С, D, представляющих наиболее типичные условия естественного (В, С и D) и искусственного (А) освещения.

Цветовые измерения на основе кривых сложения

Второй путь цветовых измерений (Ц. и.) на основе кривых сложения — это анализ излучения с помощью 3 приёмников света (См. Приёмники света), характеристики спектральной чувствительности (См. Спектральная чувствительность) которых совпадают с кривыми сложения. Каждый такой светоэлектрический преобразователь выполняет действия перемножения 2 спектральных функций и интегрирования произведений, в результате чего на его выходе электрический сигнал равен (при соответствующей калибровке прибора) одной из ЦК. Подобные цветоизмерительные приборы называются фотоэлектрическими (или объективными) колориметрами. Они оценивают результирующее излучение, учитывая как избирательное отражение (или пропускание) несамосветящихся (c проходящим светом) предметов (например, линз), так и освещение, т. е. прибор «видит» то, что видит глаз. Основной трудностью при изготовлении фотоэлектрических колориметров является достаточно точное «формирование» кривых сложения, для чего обычно подбирают соответствующие Светофильтры. Если прибор предназначен для работы с кривыми сложения x̅, , то наиболее трудно сформировать двугорбую кривую x̅ (рис. 2). Обычно каждая из её ветвей формируется отдельно; тогда прибор содержит 4 канала (светофильтра). Иногда в колориметрах используют др. ЦКС, все кривые сложения в которой одногорбые. Один из каналов колориметра одновременно может служить Яркомером. Часто в таких приборах предусматривается расчёт координат цветности. Максимальная точность цветовых измерений фотоэлектрическими колориметрами по цветности в координатах х, у составляет от 0,002 до 0,005 (относительные единицы измерения).

Прямое определение цветовых координат

SRGB цветовой треугольник, показано как подмножество x, y пространства, пространства цветности, основанный на колориметрии CIE 1931. Цветной треугольник является плоскостью расположения цветов в треугольнике, на основе сочетанием трех основных цветов RGB (красный, зелёный, синий) по углам. Организации цветов, например, вокруг системы из основных цветов: красного, жёлтого и синего были до теории аддитивного синтеза цвета. В современной x, y диаграмме большой треугольник, ограниченный воображаемым предварительным выбором (праймериз) X, Y и Z имеет углы (1,0), (0,1) и (0,0) (см. рис.4, Цветовые координаты (версия Миг)), соответственно; при этом SRGB определяет цветность красного, зеленого и синего первого предварительного подбора основных цветов. Треугольник представляет набор первичных цветов; цвета в пределах этого треугольника могут быть воспроизведены путем смешивания основных цветов. Цвета вне цветового треугольника поэтому показаны здесь как серый цвет. Предварительный выбор цветов и D65 и чёрно-белая точка SRGB показаны. (Эталон МКО D65 (иногда пишется D65, что является широко используемым стандартным источника света и определяется Международной комиссии по освещению (CIE) (МКО). Это часть D серии осветительных устройств, которые пытаются изобразить стандартное освещение в условиях на открытом воздухе в различных частях мира).

Другой принципиальной возможностью цветовых измерений является прямое определение цветовых координат — ЦК.

Но это возможно не всегда, т.к. в общем случае цветовые ощущения возбуждает световое излучение произвольного спектрального состава, а ЦК физически не существует. Прямое измерение ЦК возможно в трёхцветных аддитивных устройствах создания цвета (RGB), используемых, например, для воспроизведения цветных изображений. Основные цвета такого устройства определяют ЦКС, и их количества в смеси, дающей некоторый цвет, и есть ЦК этого цвета в ЦКС устройства. Пример такого устройства — трёхцветный Кинескоп, в котором раздельное управление свечениями 3 люминофоров (См. Люминофоры) обеспечивает получение всего множества цветов, цветности которых заключены в пределах цветового треугольника, определяемого основными цветами кинескопа (цветностями свечений люминофоров, см. Цветное телевидение). Для непосредственного измерения количеств 3 основных цветов в цвете смеси, воспроизводимом на экране кинескопа, т. е. ЦК в ЦКС кинескопа, можно использовать фотоэлектрический приёмник излучения с произвольной спектральной чувствительностью, лишь бы она не выходила за пределы видимого спектра. Измерительным прибором, подключенным к такому приёмнику, достаточно поочерёдно замерить интенсивности свечения отдельных люминофоров кинескопа. (При измерении интенсивности свечения красного люминофора «отключаются» лучи, возбуждающие зелёный и синий цвета, и т.д.) Калибровка подобного прибора состоит в снятии его показаний при поочерёдном измерении интенсивностей свечения 3 люминофоров после установки на экране опорного белого цвета, т. е. цвета с опорной цветностью ЦКС кинескопа и максимальной яркостью. В дальнейшем при измерениях разных цветов показания прибора делятся на показания для соответствующих основных цветов при опорном белом цвете. Результаты такого деления и будут ЦК в ЦКС кинескопа. Опорный белый цвет при калибровке устанавливается как можно более точно с помощью других приборов (спектрофотометра, фотоэлектрического колориметра) или визуально по специальному эталону белого цвета. Точность установки опорного белого цвета при калибровке определяет точность последующих Ц. и. (цветовых измерений). Получить значения ЦК в др. ЦКС (например, международных) можно, пересчитав показания прибора по формулам преобразования ЦК. Для вывода пересчётных формул нужно знать координаты цветности опорного белого цвета и основных цветов данного кинескопа, которые измеряют каким-либо др. методом. Большое преимущество такого непосредственного измерения ЦК по сравнению с Ц. и. при помощи фотоэлектрического колориметра заключается в отсутствии необходимости формировать определённые кривые спектральной чувствительности фотоприёмника. Ц. и. по описанному способу можно выполнять и по полному цвету свечения экрана, без отключения лучей, возбуждающих отдельные люминофоры. В этом случае в приборе должно быть 3 светофильтра с произвольными, но различающимися спектральными характеристиками. В таком приборе каждый отсчёт представляет собой сумму 3 отсчётов однофильтрового прибора для всех 3 отдельных цветных свечений. Чтобы получить значения ЦК по 3 отсчётам трёхфильтрового прибора, используют пересчётную матрицу, элементы которой определяются при калибровке прибора. Калибровка состоит в поочерёдных измерениях каждым из каналов прибора каждого из цветных свечений люминофоров в отдельности после установки на экране опорного белого цвета. Указанный пересчёт, а также переход от ЦК в ЦКС кинескопа к международной ЦКС в приборе описываемого типа может производиться автоматически, с помощью специально встроенной электрической схемы. Т. о. можно получать отсчёты прямо в ЦКС (цветовая координатная система) кинескопа или в международной ЦКС.

Метод визуальной колориметрии

ЦК (цветовые координаты) определяют также при измеренном цвете визуальными колориметрами. Наблюдатель, регулируя количества 3 основных цветов такого прибора, добивается зрительного тождества цвета смеси этих цветов и измеряемого цвета. Затем вместо последнего измеряют цвет смеси. А её ЦК есть просто количества основных цветов колориметра, отнесённые к количествам этих же цветов, входящих в смесь, которая даёт опорный белый цвет ЦКС колориметра. Измерить количества основных цветов в визуальном колориметре ещё легче, чем в цветном кинескопе. Достаточно прочесть показания 3 шкал, отградуированных по раскрытию щелей, пропускающих световые потоки соответствующих цветов к полю сравнения. Откуда при использовании визуальных колориметров измеряется косвенно цвет образца, а его «метамер» — восприятие цвета смеси трёх основных цветов колориметра. Процесс зрительного уравнивания двух цветов служит при этом для получения такого метамера цвета образца, ЦК которого можно легко измерить. Достоинством визуального колориметрирования является высокая точность Ц. и. Недостатком же является то, что получаемые результаты действительны для конкретного (выполняющего зрительное уравнивание двух цветов), а не для стандартного наблюдателя. Кроме того, этим методом трудно измерять цвета не отдельных образцов, а предметов.

Принцип зрительного сравнения измеряемого цвета с цветом, ЦК которого известны или могут быть легко измерены, используется также при Ц. измерении с помощью цветовых атласов. Последние представляют собой наборы цветных образцов в виде окрашенных листов бумаг, которые систематизированы в определённом порядке. При сравнении с измеряемым цветом подбирается образец из атласа, наиболее близкий к нему. Измеренный цвет получает наименование этого образца в соответствии с принятой в данном атласе системой обозначений. Для выражения его в международной ЦКС все образцы атласа заранее измеряются в этой системе при определённом освещении. Измеряемые цвета желательно наблюдать при том же освещении. Цветовые атласы позволяют измерять или уточнять цвета предметов (например, автомобилей при их ремонте согласно номеру цвета в атласе), а не только специальных образцов, но дискретность набора цветов в атласе снижает точность измерений, которая дополнительно понижается из-за того, что условия зрительного сравнения здесь хуже, чем при визуальном колориметрировании. В СССР использовали цветовые атласы Рабкина и ВНИИМ (АЦ-1000), в США широкое распространение получили измерения по атласу Манселла (Мензелла). Цвета измеренные с помощью цветовых атласов являются прикидочными и могут с успехом производиться там, где большая точность не нужна или, где неудобно применять другие методы.

Выражение цвета в определённой ЦКС, т. е. при задании его ЦК (или яркости и координат цветности), универсально и наиболее употребительно. Но прибегают и к др. способам количественного выражения цвета. Примером может служить только что описанное выражение цвета в системе какого-либо цветового атласа. Ещё один такой способ — выражение цвета через его яркость, преобладающую длину волны и колориметрическую чистоту цвета. (Последние два параметра характеризуют цветность.) Достоинство этого способа заключается в близком соответствии 3 перечисленных параметров цвета привычным субъективным его характеристикам: светлоте, цветовому тону и насыщенности.

Более удобно характеризовать цветность одним числом. Но её двумерность требует для её выражения в общем случае двух чисел. С точки зрения трёхкомпонентных моделей — для некоторых совокупностей цветностей (линий на графике цветностей) можно использовать одномерное выражение.

• Первая такая совокупность — чистые спектральные цвета и чистые пурпурные цвета, цветности которых определяются значениями преобладающей длины волны.

• Второй совокупностью, для которой возможно одномерное выражение, являются цветности излучения абсолютно чёрного тела (См. Абсолютно чёрное тело), используемые для характеристики источников освещения с цветностями свечения, близкими к цветности белого цвета. Величина, определяющая положение точки на линии цветностей излучения чёрного тела (и цветности упомянутых источников), — Цветовая температура, т. е. температура в градусах Кельвина абсолютно чёрного тела, при которой оно имеет данную цветность. Тем не менее этот метод находит ограниченное применение.

Линейное уравнение цветного зрения и цветового пространства

Рис.3. Нормализованные спектры чувствительности фотопигментов колбочек сетчатки глаза при цветном зрении в условиях дневного освещения.

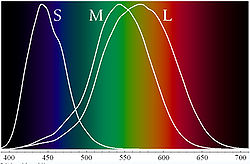
В итоге, из условия, что пучок света может быть составным, состоящим из излучений многих различных длин волны, определять степень, в которой физический цвет C в H_цвет стимулирует каждую клетку колбочки , мы должны вычислить интеграл (относительно w), по интервалу [W_min,W_max], из уравнения:

C (w) *s (w), C (w) *m (w), и C (w) *l (w) (см. рис.3).

Тройные из получающихся чисел связываются каждым «физическим» цветом C (который является областью в H_цвет) к специфическому воспринятому цвету (который является единственным пунктом в R³_цвет). Т.е. при оппонентном отборе трёх основных цветов S,M,L наиболее ярких из числа многих цветов сфокусированных на колбочки лучей предметных точек. Эта функция, как легко можно заметить, является линейной (как уравнения первой степени). Может также быть легко замечено, что много различных областей в «физическом» месте H_цвет могут все привести к тому же самому единственному воспринятому цвету в R³_цвет.

Таким образом, воспринятый цвет не уникален для одного физического цвета. То есть природа цветного зрения подчиняется принципу трёхкомпонентного цветного зрения (на базе трёх основных цветов спектра света RGB при работе колбочек в условиях дневного освещения и математически выражается линейным уравнением.(В отличие от нелинейной теории цветного зрения, по которой в цветном зрении участвуют блоки колбоча+палочка, что неправильно. (См. Ретиномоторная реакция фоторецепторов (версия Миг)).

В итоге человеческое цветное восприятие определено определенной, групповой линейной картографией от бесконечномерного места Hilbert Hцвет к 3-мерному Евклидовому месту en:Euclidean_spaceR³_цвет.

И наше ощущение цвета привело к появлению понятия цветового пространства, которое выражается математической цветовой моделью представления цвета, которая основана на использовании цветовых координат.

См. также

• Цветовые пространства LAB
• Стандартные источники света

Литература

• Гуревич М. М., Цвет и его измерение, М. — Л., 1950;
• Кривошеев М. И., Кустарев А. К., Световые измерения в телевидении, М., 1973;
• Нюберг Н. Д., Измерение цвета и цветовые стандарты, М., 1933;
• Wright W. D., The measurement of colour, 3 ed., L., 1964;
• Wyszecky G., Stiles W. S., Color science, N. Y., 1967. А. К. Кустарёв.