Линейное уравнение цветного зрения и цветового пространства
Линейное уравнение цветного зрения и цветового пространства — основано на открытиях явления зрения, цветного зрения, где доказан принцип трихроматизма цветного зрения, при котором визуальное цветное зрение в животном мире является главным фактором приспособления всех живущих к окружающей среде, условием выживаемости благодаря способности зрительной системы воспринимать изображения объектов в цвете.
Введение[править | править код]

У людей воспринимаемый цвет может быть смоделирован как три числа: степень стимуляции каждого из 3-х типов колбочек (то есть клетками, состоящими из трёх колбочек с зонами условного восприятия диапазона основных цветов RGB). Таким образом о человеческом восприятии цвета можно думать как о векторе в 3-мерном Евклидовом пространстве. Мы называем этот вектор R³цвет.[1]
Линейная функция цветного зрения[править | править код]
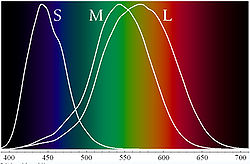
Начиная с каждой длины волны — w стимулирует каждый из 3 типов клеток колбочек сетчатки глаза до известной степени, и эти степени могут быть представлены 3 функциями клеток-колбочек s (w), м. (w), l (w) ответу S, М., L, соответственно. (см. рис.8). При этом каждая колбочка, сфокусированный на неё пучок лучей предметной точки, оппонентно выделяет самый яркий один из основных цветов S,M,L (синий, зелёный, красный ( RGB) в виде эквивалентных биосигналов в мозг. Здесь выделенные биосигналы S,M,L = RGB составляют ответы колбочек как точки линейных функций s (w), м. (w), l (w).
Откуда визуальное цветное зрение — основа современных концепций в том числе и математики цветного зрения.
Цветовое зрение, происходящее в зрительной системе инициируется поглощением света с помощью трех различных спектральных классов «шишек» (колбочек). Следовательно, цветовое видение описывается как трёхвариантное восприятие осноных цветов или как восприятие, ощущение цвета. Первоначально психофизические исследования показали, что цвета могут быть настроены на использование трех различных систем (праймериз). В 1802 году, Томас Молодых предложил модель, по которой восприятие цвета может быть закодировано на три основных цвета S,M,L фоторецепторов, но не на кодировании тысяч цветовых рецепторов для отдельных цветов.[2] (См. Визуальное цветное зрение (версия Миг)).
Наконец, так как пучок света может быть составным, состоящим из излучений многих различных длин волны, определять степень, в которой физический цвет C в Hцвет стимулирует каждую клетку колбочки сетчатки глаза, мы должны вычислить интеграл (относительно w), по интервалу [Wmin,Wmax], из:
- C (w) *s (w), C (w) *m (w), и C (w) *l (w) (см. рис.3).
Тройные из получающихся чисел связываются каждым «физическим» цветом C (который является областью в Hцвет) к специфическому воспринятому цвету (который является единственным пунктом в R³цвет). Т.е. при оппонентном отборе трёх основных цветов S,M,L наиболее ярких из числа многих цветов сфокусированных на колбочки лучей предметных точек. Эта функция, как легко можно заметить, является линейной. Может также быть легко замечено, что много различных областей в «физическом» месте Hцвет могут все привести к тому же самому единственному воспринятому цвету в R³цвет. То есть воспринятый цвет не является единственным для одного физического цвета. То есть природа цветного зрения подчиняется принципу трёхкомпонентного цветного зрения (на базе трёх основных цветов спектра света [[RGB]] при работе колбочек в условиях дневного освещения и математически выражается линейным уравнением.
В отличие от исходных данных линейных уравнений трихроматизма, где основные три цвета S,M,L (принятых как три координаты линейных графиков), где синий цвет S (колбочки-S), в нелинейной модели цветного зрения принадлежит фоторецептору палочке сетчатки глаза. Откуда все графики цветного зрения построены в нелинейной теории зрения из условия , что колбочка якобы способна воспринимать только красно-зелёные лучи, а палочка дополняет недостаток колбочки воспринимать синие цвета, работая с ней в паре. И соответственно все выводы, методика исследований и все данные получены из нелинейной теории цветного зрения. В ней модели цветного зрения строятся на основе искусственных данных колориметрии в отрыве от работы зрительной системы. При этом игнорируется:
- ретиномоторная реакция фоторецепторов,
- наличие доказанной синей колбочки (см. Тропы булочек (S-cone) (версия Миг), Денситометрия (версия Миг), Денситометр (версия Миг), Денситометрия и фотопигменты колбочек),
- принцип оппонентного выделения колбочкой/колбочками при сфокусированной на неё (них) предметной точки изображения самых ярких основных лучей спектра биосигналов S,M,L = RGB (красный, зелёный, синий), отправляемых в мозг (см.Теория оппонентного цветного зрения),
- Работа зрительной коры.
Откуда основной вывод нелинейной теории зрения, что в цветном зрении работает блок колбочка+палочка не правильный и не признан во всём мире.
В любом случае цветное зрение — трёхкомпонентное и происходит (с оппонентным отбором трёх самых ярких основных цветов S,M,L спектра света RGB) при работе колбочек в условиях дневного освещения и математически выражается линейным уравнением.
Т.о. человеческое цветное восприятие происходит с определенной, групповой линейной картографией от бесконечномерного места Hilbert Hцвет к 3-мерному Евклидовому месту en:Euclidean_spaceR³цвет.
Наше ощущение цвета привело к появлению понятия цветового пространства, которое выражается математической цветовой моделью представления цвета, которая основана на использовании цветовых координат.
Представления цвета в зрительной коре и цветовой модели[править | править код]



Линейное уравнение цветного зрения, цветового пространства — комплекс представлений для математического описания «физического цвета», которые мы видим, как комбинации чистых спектральных цветов из видимого диапазона электромагнитного излучения. Существует бесконечное множество различных спектральных цветов, большинство из которых не имеют названий (см. Наименование цвета). Набор всех физических цветов (отражённых и прямых), которые мы воспринимаем, можно выражать через математические векторы в бесконечномерном векторном пространстве. Более узко — в гильбертовом пространстве (en:Hilbert_space). Его называют цветовым пространством, Hcolor. Т.е. математические концепции в Гильбертовом пространстве, названного в честь Давида Гильберта, обобщаются понятием как Евклидово пространство. Это расширяет методы векторной алгебры и исчисления от двухмерной Евклидовой плоскости до трехмерного пространства, а также для пространства любого конечного или бесконечного числа измерений.
Место воспринимаемых видимых лучей (физических или электромагнитных колебаний) — цветов (биологических) можно интерпретировать как симплексы (геометрические фигуры, являющаеся n-мерными обобщениями треугольников) в (математическом) конусе, вершины которого — спектральные цвета. Белый цвет (свет) располагается на оси (в точке пересечения оси и основания конуса) (en:Centroid) симплекса, черно-белый — только на оси конуса (внизу — чёрный, вверху — белый, между ними — оттенки серого), и монохроматические цвета, связанные с осью с любой данной вершиной где-нибудь по линии оси от этих вершин в любых плоскостях сечений конусов в зависимости от их яркости. (Максимально яркие, насыщенные цвета спектра располагаются в плоскости наибольшего диаметра сечений конусов, в середине оси)(см. рис.3b).
Элемент C Hcolor является функцией из диапазона видимых осознаваемых ощущений от длин волны, в интервале реальных чисел [Wmin,Wmax], с соответствием каждой длине волны w [Wmin,Wmax] — интенсивность C(w) — ответы колбочки от двух излучающих спектров.
Трёхкомпонентная цветовая модель XYZ[править | править код]

Треугольник Cb-Cg-Cr это только xy=(0,0),(0,1),(1,0), треугольник CIE xy— цветность пространства. Линия, соединяющая Cb и Cr это линия нулевой яркости на цветовом графике (alychne).
Обратите внимание, что спектральный локус проходит через rg=(0,0) на 435.8 нм, через rg=(0,1) в 546.1 нм и через rg=(1,0) при 700 нм. (По старой системе применялось цветовое пространство RGB и рассчитывалось без учёта линейной функции, а область полученной цветовой палитры была внутри треугольника с углами в точках 430 нм, 540 нм и 570 нм).
Значение же энергии точки (E) при rg=xy=(1/3,1/3) равное. (См. также XYZ (цветовая модель), Цветовые координаты)
CIE XYZ — линейная 3-компонентная цветовая модель, созданная на результатах измерения характеристик человеческого глаза. Она построена на основе зрительных возможностей так называемого «стандартного среднестатистического наблюдателя». Или гипотетического зрителя, возможности которого были тщательно изучены и зафиксированы в ходе длительных исследований человеческого зрения, которые были проведенны комитетом CIE (фр. Commission Internationale de l'Eclairage).
Как доказано (см. Лаборатория Р.Е.Марка (версия Миг)), цветное зрение человека обусловлено работой трех разновидностей экстерорецепторов на сетчатке глаза, c максимумыми спектральной чувствительности в области 420, 534 и 564 нм (см. Колбочки сетчатки глаза (версия Миг) , что соответствует синему, зелёному и красному (хотя в литературе обычно пишут "жёлтому") цветам. Однако в настоящее время эти данные уточнены и согласно (рис.2a) они составляют:435.8 нм, 546.1 нм и 700 нм. Они являются базовыми, все остальные тона воспринимаются как их смешение в определенной пропорции (см. Аддитивный синтез цвета). Например, чтобы получить желтый цвет, совсем необязательно воспроизводить его истинную длину волны 570—590 нм, достаточно создать такой спектр излучения, который возбуждает рецепторы глаза сходным образом. Это явление называется метамерией.
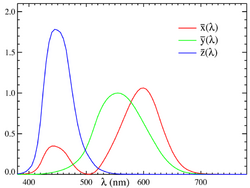
Комитет CIE провел множество экспериментов с огромным количеством людей, предлагая им сравнивать различные цвета, а затем с помощью совокупных данных этих экспериментов построил так называемые функции соответствия цветов (color-matching functions) и универсальное цветовое пространство (universal color space), в котором был представлен диапазон видимых цветов, характерный для среднестатистического человека.
Функции соответствия цветов — это значения каждой первичной составляющей основного цвета спектра — красной, зеленой и синей, которые должны присутствовать, чтобы человек со средним зрением мог воспринимать все цвета видимого спектра. Этим трем первичным составляющим были поставлены в соответствие координаты X, Y и Z. (На них откладываются соответственно значения основных цветов S,M,L КЗС).
Основное свойство, присущее этой системе — положительная определенность — любой физически ощутимый цвет представляется в системе XYZ только положительными величинами. С другой стороны, не всем точкам в пространстве XYZ соответствуют реальные цвета в силу неортогональности функций соответствия цветов.
Говоря об «эталонных» оттенках, часто говорят только о паре x, y, считая z = 1-x-y.
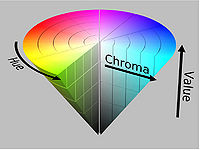
Говоря о «яркости» цвета (например, для перевода изображения в чёрно-белое), часто имеют в виду величину Y. Цветовая система Манселла (основа построения цветовых моделей), где, например, показан круг при значении чёрно-белой оси Y (value) = 5, хроме = 6, нейтральные значения равны от 0 до 10, сегмент круга (диапазон хромы) при тоне 5PB и значении Y = 5. Принцип работы заключается во вращении кругов с полутонами chroma с осью вращения яркости цвета value, и статистический наблюдатель увидит цвета плоскостей вращения на разных высотах относительно оси value (0-10) от белого до чёрного. (Например, в плоскости вращения с координатой 10 расположены в нужном количестве цвета красный, зелёный, синий, что даёт самый яркий цвет — белый. В конусных моделях (см.рис.3а) координата 10 окружность в пределе переходит в белую току вершины конуса). (Cм. рис.1m).
См. также[править | править код]
Сноски[править | править код]
| Текущая версия статьи о цвете. Помогите Традиции, исправьте и дополните её. |