Комплекс "Хеопс-Хефрен-Микерин"="Атом водорода"12

Материал из свободной русской энциклопедии «Традиция»
Перейти к навигации Перейти к поиску
Periss icon.png Первоначальные исследования
Этот раздел статьи является первичным источником части изложенной в нём информации, содержа первоначальные (или ранее не известные широкому кругу читателей) исследования.

Квантование диска и образование планет[править | править код]

К вопросу образования планет обращались и обращаются многие исследователи и поэтому считаю, что детального и подробного рассмотрения этого вопроса делать нет никакой необходимости.

В пункте "Первое приближение" было проделано квантование Солнечной системы.

Ввиду того, что образование Солнечной системы - процесс длительный, то, естественно, и квантование тоже должно начинаться с момента образования ядра глобулы, т.е. когда возникает реальная масса ядра Mяд, которая затем входит в уравнение Rn = 4 h'2 n2 / γ Mc (Rn - среднее расстояние планет от Солнца, n = 1,2,3,..., γ - постоянная всемирного тяготения) в качестве Mc. Следовательно, квантование должно быть применено для всей толщины диска, что и рассматривается далее.

В различных вычислениях и расчетах все время упоминалось уравнение Rn = n2 Rм (Rм - среднее расстояние Меркурий-Солнце), хотя Венера и Земля не подчиняются ему. Это же уравнение может быть записано и в виде Rn = N2 r1' (r1' = 2 h' / c), где N = 1,2,3,... , r1' - предельная гравитационная орбита планеты, c - скорость света. Тогда уже все планеты без исключения будут удовлетворять условию квантования.

Следует также напомнить, что газопылевое облако не остается неизменным в пространстве и во времени: возникают и разрушаются многочисленные большие и малые сгущения; часть сгущений падает на ядро и растут большие сгущения, давая начало зарождению будущих планет, спутников планет и другим небесным телам.

Группа III (клетки 5,8,9) характеризует связь между i и α соответствующими уравнениями и относится, в первую очередь, к зарождающимся крупным сгущениям.

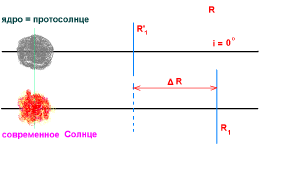
Рассмотрим сечение такого сгущающегося слоя вещества вблизи плоскости i = 0° - сечение диска в средней части. Масштаб расстояний на рисунке не соблюден.

Начальный этап сгущений

Длинные красные стрелки (слева) - электромагнитное и корпускулярное излучения протосолнца. Плоскость эклиптики (плоскость диска Галактики) - i = 0°. R1, R2, R3, ... - расстояния до устойчивых орбит, согласно Rn = N2 r1' (Rn = n2 Rм). Синие и черные короткие стрелки на i = 0°, вблизи и вдали от нее, указывают на направление движения вещества.

Слово "диск" не характеризует форму области образования устойчивых орбит. Это просто дань предыдущим теориям происхождения планет и Солнца, и пока будем придерживаться этого слова.

Увеличивающаяся масса ядра Mяд достигает современного значения Mc и поэтому перестает быть переменной величиной, т.е. Mяд → Mc = const.

В результате взаимодействия сгущений (столкновение, вращение вокруг центрального сгущения и т.д.) может меняться направление вращения вокруг своей оси центрального сгущения, угол наклона плоскости орбиты к i = 0°, скорость вращения вокруг своей оси и т.п.

Хотя мы упоминали, что Mc = const, но все-таки для различных расчетов надо указывать, что масса протосолнца (= Mc) уменьшается вследствие электромагнитного и корпускулярного излучений, что, в соответствии с уравнением

Rn = n2 Rм = n2 (4 h'2 / γ Mc),

приводит к увеличению Rn. Кроме того, эти излучения начинают действовать на газопылевое вещество и сгущения, оказывая на них давление. Поэтому легкое вещество начинает перемещаться по всему объему от центральной части к периферии и в наибольшей степени вблизи i = 0° согласно функции разделения.

Необходимо здесь также добавить, что и до образования протосолнца, т.е. когда масса ядра Mяд увеличивалась от 0 и до Mc, ΔRn (изменение расстояния для определенного n) была значительной величиной. Орбиты Rn в этом случае как бы "перемещались" из ∞ к каким-то значениям. Можно также сказать, что в момент образования протосолнца эти Rn имели минимальные значения. После достижения глобулой Mяд = Mc и вплоть до смерти Солнца (экстраполяция из-за постоянного уменьшения массы Солнца Mc) скорости увеличения Rn и, возможно, выноса вещества в плоскости i = 0° на периферию, остаются почти неизменными.

На периферии диска вследствие увеличения концентрации вещества глобулы к i = 0°, выноса вещества вблизи плоскости i = 0° и наличия электромагнитного и корпускулярного давления, образуется, возможно, так называемое колцеобразное облако Оорта, которое может служить источником комет и других небесных тел.

Образование больших сгущений происходит примерно так же, как шло образование центрального сгущения - протосолнца. Поэтому, если первоначальная масса глобулы большая, то возможен и процесс образования не планет, а второго протосолнца, т.е. может возникнуть и двойная звезда. Тогда вероятность образования устойчивых планетных орбит и самих планет резко уменьшится.

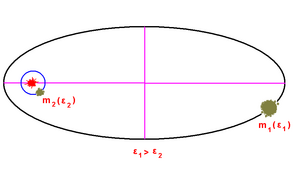
И немного об орбитах. В Солнечной системе современные планетные орбиты - короткофокусные эллипсы. Распределение планетного вещества (массы планет) вблизи плоскости эклиптики неравномерное. Следовательно, эта неравномерность создалась вследствие первоначальной неравномерности газопылевого вещества диска, т.е. за счет давления со стороны Солнца (электромагнитное и корпускулярное излучения) и притока вещества к i = 0° из области устойчивых орбит (вследствие гравитационного притяжения).

Влияние эллиптичности орбиты на образование сгущений

Но неравномерность может быть и в случае большой эллиптичности планетной орбиты в период образования. Если эксцентриситет орбиты тела m2 большой, то это тело в процессе образования "впитывает" в себя больше окружающего газопылевого вещества и можно написать: m2 ~ e. Тогда количество таких тел (= будущие планеты) в звездной системе должно быть небольшим. Поэтому будет проявляться такая связь:

если орбиты тел обладают малым e (≈ окружность), то может образовываться максимальное количество планет, а если эксцентриситеты орбит тел e большие, то - минимальное количество планет.

Не рассматривался еще случай, когда сгущение происходит по "вине" прилета чужеродного тела в Солнечную систему. В этом случае процесс сгущения может идти быстрее и поэтому возраст данной будущей планеты, например, может быть равен или даже больше возраста протосолнца.

Образование спутников планет максимально в том месте, где вещества много и занимаемый им объем велик. Может быть два основных варианта:

  • отдельное их образование (вдали от центрального планетного сгущения) и затем их захват:
столкновение с центральным сгущением и гибель спутника;
распад спутника вблизи центрального сгущения и образование кольца;
устойчивая орбита около центрального сгущения;
  • совместное образование, т.е. образование вблизи центрального сгущения или деление на части одного сгущения с образованием нескольких спутников.

Квантование Солнечной системы на:

Будущее Солнечной системы и "бегство" Разума от гибели[править | править код]

Проводить описание современного этапа развития (= жизнь) Солнечной системы нет никакой необходимости, ибо его изучает целый комплекс наук и поэтому сразу же перейдем к будущему Солнечной системы.

Как известно, любой объект (= система) имеет свое начало и свой конец жизни. Поэтому и любая звезда имеет свой конец - "смерть". "Смерть" - в смысле прекращения электромагнитного и корпускулярного излучений. После "смерти", в зависимости от массы звезды, образуется белый карлик или нейтронная звезда (пульсар) - черная дыра. Масса звезды перед "смертью" оказывается заметно меньше той, что была при рождении, т.е. существует дефект массы звезды. Согласно квантованию Солнечной системы, это будет означать, что в уравнении для планетных орбит

Rn = n2 R1 = n2 (4 h'2 / γ Mc) ,

где R1 - радиус орбиты Меркурия, необходимо учитывать массу Солнца Mc в моменты рождения и "смерти". При уменьшении Mc радиусы (= большие полуоси) планетных орбит увеличиваются. Так как момент "смерти" Солнца мы не знаем как точно определять, то "передвинем" рассмотрение на современный этап жизни Солнечной системы.

Определим изменение планетных орбит Солнечной системы только вследствие электромагнитного излучения. Предполагая, что Солнце излучает энергию на всех длинах волн A = 4×1026 Дж / с и что излучение постоянно во времени, мы можем определить увеличение радиуса орбиты Меркурия за год. Современное значение массы Солнца Mc = 1,9×1030 кг. Тогда за время существования - Tc - Солнце потеряет массу, равную

Mизл = A Tc / c2 ,

где c - скорость света.

Следует различать истинное время жизни Солнца: оно складывается из времени жизни ядра глобулы от момента его возникновения и до превращения ядра в протосолнце - Tяд и Tc - времени жизни Солнца от момента "протосолнце" и до настоящего времени. Значит

Tc' = Tc + Tяд ,

где Tc' - полное (истинное) время жизни Солнца.

Поэтому начальная масса Солнца равна массе протосолнца:

Mc' = Mc + Mизл = Mc + A Tc / c2 .

Радиус орбиты Меркурия в начале (в момент рождения Солнца и n = 1):

R1' = 4 h'2 / γ Mc' = 4 h'2 / γ (Mc + A Tc / c2) ,

где R1' - минимальное значение радиуса орбиты Меркурия и R1' < R1. Далее следует:

Δ R = R1 - R1' = 4 h'2 / γ Mc - 4 h'2 / γ (Mc + A Tc / c2) = (4 h'2 / γ) [1 / Mc - 1 / (Mc + A Tc / c2)] = (4 h'2 / γ) [A Tc / c2 Mc (Mc + A Tc / c2)] .
Увеличение радиуса орбиты тела

Скорость изменения радиуса орбиты Меркурия за время жизни Солнца Tc:

Δ R / Tc = (4 h'2 / γ) [A / c2 Mc (Mc + A Tc / c2)] .

При Tc = 5 млрд. лет , A = 4×1026 Дж/с и c = 3×108 м/с имеем:

A Tc / c2 = (4×1026 × 2×1017) / 9×1016 = 1027 (кг) << Mc

и поэтому

Δ R / Tc = (4 h'2 / γ) [A / (Mc c)2] .

Для Меркурия эта формула дает:

Δ R / Tc = 4 ×(1,4×1015)2 × 4×1026 / 6,7×10-11 × (1,9×1030 × 3×108)2 = 1,5×10-10 (м/с) = 0,48 см/год .

Для Марса (n = 2) получаем:

Δ R / Tc = 22 × 0,48 = 1,92(см/год),

т.е. чем дальше планета от Солнца (n растет), тем больше Δ R / Tc .

Если произвести аналогичные расчеты с учетом корпускулярного излучения, то получим соответственно

Δ R / Tc > 0,48 см/год (> 1,92 см/год) .

Солнце относится к "спокойным" и долгоживущим звездам и, следовательно,

A Tc / c2 << Mc .

"Спокойная" жизнь Солнца = спокойное развитие цивилизаций в Солнечной системе. Полученное соотношение Δ R / Tc дает возможность определять возраст Tc Солнца (от протосолнца и до настоящего момента):

Tc = γ (Mc c)2 Δ R / 4 h'2 A .

Более точное значение Tc должно получаться с учетом корпускулярного и гравитационного излучений Солнца. Необходимо только точно измерять Δ R и A как для Меркурия, так и для других планет.

Итак, мы пришли к выводу, что все расстояния до планетных орбит Солнечной системы увеличиваются - Солнечная система расширяется.

Обратимся еще раз к соотношению Δ R / Tc. Если Δ R и Tc равны const для какой-то одной орбиты планеты Солнечной системы, то это соотношение будет являться средней скоростью расширения именно данной орбиты, т.е.

Δ R / Tc = vср = const .

Тогда для Меркурия получаем

(vср)1 = (4 h'2 / γ) [A / (Mc c)2] .

Для n - ой орбиты:

(vср)n = n2 (4 h'2 / γ) [A / (Mc c)2] - средняя скорость перемещения n - ой орбиты за время Tc .

n2 выражаем из уравнения Rn = n2 R1 :

n2 = Rn / R1 .

Окончательно получаем:

(vср)n = (4 h'2 / γ) [A / (Mc c)2 R1] Rn

или

(vср)n = (vср)1 Rn / R1 - средняя скорость удаления n - ой орбиты (Rn) от Солнца.

Если наблюдатель будет находиться не на Солнце, а на R1, то

(vср)n' = (vср)n - (vср)1 = (4 h'2 / γ) [A / (Mc c)2] (Rn / R1) - (4 h'2 / γ) [A / (Mc c)2] = (4 h'2 / γ) [A / (Mc c)2] (Rn / R1 - 1) .

Так как Rn >> R1, то

Rn / R1 >> 1 и (vср)n' = (4 h'2 / γ) [A / (Mc c)2] (Rn / R1) .

Обозначая

(4 h'2 / γ) [A / (Mc c)2 R1] = B ,

получаем

(vср)n' = B Rn - средняя скорость перемещения n - ой орбиты (Rn) относительно наблюдателя на R1 за время Tc.

Подставляя известные данные, получим:

B = 1,5 × 10-10 / 5,8 × 1010 = 2,5 × 10-21 (1/c) .

В этом уравнении для расчетов Rn = R1 = Rм = 5,8×1010 м (Меркурий), (vср)n' = vср = 1,5×10−10 м/с.

Если R1 = const, то и B = const и мы получаем "закон Хаббла" для Солнечной системы.

Rn / (vср)n' = 1 / B = tn .
t_n = 1 / B = 1 / 2,5 × 10-21 = 4 × 1020 c = 1,3 × 1013 лет = 13 000 млрд. лет .
Rn / (vср)n' = Rn / (Δ Rn / Tc) = tn

и

Rn = tn Δ Rn / Tc .

Рассмотрим частный случай. Если Rn (расстояние до n - ой орбиты) = Δ Rn (изменение n - ой орбиты от 0 и до Rn, т.е. Δ Rn), то тогда имеем:

tn = Tc (возраст Солнца).

Образование планет на:

Солнечная система на:

Страница: 0 , 1 , 2 , 3 , 4 , 5 ,6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15 , 16 , 17 , 18

Примечания[править | править код]

См. также[править | править код]

Ссылки[править | править код]

Литература[править | править код]

Источник — https://traditio.wiki/w/index.php?title=Комплекс_%22Хеопс-Хефрен-Микерин%22%3D%22Атом_водорода%2212&oldid=853907