Комплекс "Хеопс-Хефрен-Микерин"="Атом водорода"9

Материал из свободной русской энциклопедии «Традиция»
Перейти к навигации Перейти к поиску
Periss icon.png Первоначальные исследования
Этот раздел статьи является первичным источником части изложенной в нём информации, содержа первоначальные (или ранее не известные широкому кругу читателей) исследования.

[править | править код]

Ранее мы вели расчеты и вычисления, исходя из того, что есть атом водорода, т.е. протон и электрон уже находятся в связанном состоянии. Нисколько при этом не учитывалась "история" создания атома водорода.

Когда протон и электрон находятся далеко друг от друга - за пределами взаимовлияния - их ничто не связывает. При сближении друг с другом они начинают взаимодействовать. Поэтому для создания "своего дома" - атома водорода - им необходим "строительный материал" в форме электромагнитной энергии. Эту энергию они берут из окружающего пространства. Можно сказать, что, приобретая эту энергию, они как бы "утяжеляются", т.е. изменяются их собственные массы. Поэтому и вычисленная полная энергия электрона - это энергия их связи друг с другом. И тогда на каждого "члена семьи дома" будет приходиться энергия, равная (закон сохранения полной энергии):

Eсв = |E| / 2 = (1/4) me α2 c2 .

Тогда "добавочная масса" к собственным массам будет равна:

Δ m = Eсв / с2 = (1/4) me α2 .

Вследствие этого мы имеем массы:

me' = me + (1/4) me α2 = me [1 + (1/4) α2)] ,
mp' = mp + (1/4) me α2 = mp [1 + (1/4) (me / mp) α2)] .

Следовательно, в обозначении A получаем:

A = (me / mp) [{1 + (α2 / 4)} / {1 + (α2 / 4) (me / mp)}] = [mo (e) / mp] [1 / (1 - α2)1/2] [(4 + α2) / {4 + α2 (m0 (e) / mp) (1 / {1 - α2}1/2)}] .

Вычисления дают:

0,999999851684 + 0,001159513564 + 0,000000296631 - 0,000000009231 = 1,001159652648

или 1,00115965243(±21).

Вычислим снова полную энергию электрона на первой боровской орбите, учитывая:

  • скорость электрона на орбите v0 = α c, скорость смещения относительно магнитного поля vм = α2 c (вместо α2 c / 2 π) и тогда v = α c + α2 c;
  • расстояние от протона до электрона a0 + rp = a0 (1 = me/mp);
  • зависимость массы электрона от скорости: me = m0 (e) / [1 - α2 (1 + α)2]1/2 .

В результате преобразований мы получим:

E = K + П = [ α2 c2 m0 (e) / [1 - α2 (1 + α)2]1/2 ] [ (1 + α)2 / 2 - 1 / {1 + (m0 (e) / mp) [1 / {1 - α2 (1 + α)2} ] } ] < 0 .

Энергия связи:

Eсв = |E| / 2 = [ α2 c2 m0 (e) / 2 [1 - α2 (1 + α)2]1/2 ] | (1 + α)2 / 2 - 1 / {1 + (m0 (e) / mp) [1 / {1 - α2 (1 + α)2} ] } | .

"Добавочная масса" для движущихся электрона и протона будет равна:

Δ m = Eсв / c2 = [ α2 m0 (e) / 2 [1 - α2 (1 + α)2]1/2 ] | (1 + α)2 / 2 - 1 / {1 + (m0 (e) / mp) [1 / {1 - α2 (1 + α)2} ] } | .

По-прежнему считаем mp ≈ m0p. Окончательно для обозначения A имеем:

A = (me + Δ m) / (mp + Δ m) = [m0 (e) / mp] [1 / {1 - α2 (1 + α)2}1/2] [ {1 + (1/2) α2 | (1 + α)2 / 2 - 1 / [1 + (m0 (e) / mp) [1 / {1 - α2 (1 + α)2}1/2 ] | } / {1 + (1/2) α2 [m0 (e) / mp] [1 / {1 - α2 (1 + α)2}1/2 ] | (1 + α)2 / 2 - 1 / [1 + (m0 (e) / mp) [1 / {1 - α2 (1 + α)2}1/2 ] | } ] .

Вычисления по αmax дают:

0,999999851683 + 0,001159513563 + 0,000000296632 - 0,000000009231 = 1,001159652647

или 1,00115965243(±21).

В квантовании по Бору мы ввели постоянную тонкой структуры для записи скорости электрона на первой боровской орбите:

α = e2 / 4 π ε0 ħ c = e2 / 2 ε0 h c .

Принимая следующие постоянные равными:

e = 1,6021892 ×10−19 Кл,
ε0 = 8,85418782 × 10−12 Ф/м,
h = 6,626176 × 10−34 Дж·с,
c = 2,99792458 × 108 м/с ,

получаем αmin = 7,29735045×10−3. Производя снова вычисления по последней выведенной формуле, придем к результату:

0,999999851684 + 0,001159513120 + 0,000000296631 - 0,000000009231 = 1,001159652204.
(μан / μБ)ср = (1,001159652204 + 1,001159652647) / 2 = 1,001159652420 или 1,00115965242(±22).

Итак, полная формула для АММЭ состоит из геометрической и физической частей:

μан / μБ = (1 - A2) + (α / 2 π) [(1 - A)2 / (1 + A)] + A2 - α2 A / π,
A = [m0 (e) / mp] [1 / {1 - α2 (1 + α)2}1/2] [ {1 + (1/2) α2 | (1 + α)2 / 2 - 1 / [1 + (m0 (e) / mp) [1 / {1 - α2 (1 + α)2}1/2 ] | } / {1 + (1/2) α2 [m0 (e) / mp] [1 / {1 - α2 (1 + α)2}1/2 ] | (1 + α)2 / 2 - 1 / [1 + (m0 (e) / mp) [1 / {1 - α2 (1 + α)2}1/2 ] | } ] .
αmax = 7,29735321×10−3, αmin = e2 / 4 π ε0 ħ c = e2 / 2 ε0 h c = 7,2973504×10−3.

Процесс уточнения можно продолжать и далее, но для этого необходимо более точное экспериментальное значение для АММЭ из экспериментов с атомом водорода.

Аномальный магнитный момент электрона на:

Рождение - жизнь - смерть Солнечной системы[править | править код]

Изложение этого пункта ведется не последовательно (согласно названию пункта), а исходя из практических соображений.

Эволюция Солнечной системы на:

Первое уточнение третьего закона Кеплера[править | править код]

Запишем условие квантования Солнечной системы для планет с номерами m и n (не учитывая смещения перигелиев):

S1 / T1 = n h' и S2 / T2 = m h',

где S1 / T1 и S2 / T2 - запись второго закона Кеплера для этих планет, S1 и S2 - площади, описываемые радиусами-векторами планет, T1 и T2 - звездные периоды обращения планет вокруг Солнца, h' = 1,3859×1015 м2/с - гравитационная солнечная постоянная. Разделив второе уравнение на первое, получаем:

(T1 / T2) (S2 / S1) = m / n ===> T1 / T2 = (m / n) (S1 / S2).

Площади эллипсов планет S1 и S2 находим по известным формулам:

S1 = π a1 b1 = π a12 (1 - e12)1/2,
S2 = π a2 b2 = π a22 (1 - e22)1/2 ,

где a1, a2 и b1, b2 - большие и малые полуоси орбит, e1 и e2 - эксцентриситеты орбит. Тогда имеем:

T1 / T2 = (m / n) (a1 / a2)2 [(1 - e12) / (1 - e22)]1/2 .

Применяя квантование планетных орбит Солнечной системы, получаем:

a1 = n2 r1 , a2 = m2 r1 ,

где a1, a2 - средние расстояния (большие полуоси орбит) до планет с номерами n, m, r1 - радиус (среднее расстояние) первой орбиты (Меркурий). Далее имеем:

m2 / n2 = a2 / a1.

Возведя в квадрат T1 / T2, находим:

(T1 / T2)2 = (m2 / n2) (a1 / a2)4 [{1 - e12} / {1 - e22}] .

Заменяя m2 / n2, получаем:

(T1 / T2)2 = (m2 / n2) (a1 / a2)4 [{1 - e12} / {1 - e22}] = (a1 / a2)3 [{1 - e12} / {1 - e22}] .

Учитывая уточнение, сделанное Ньютоном, имеем:

(T1 / T2)2 [{Mc + m1} / {Mc + m2}] = (a1 / a2)3 [{1 - e12} / {1 - e22}] .
Эллипс

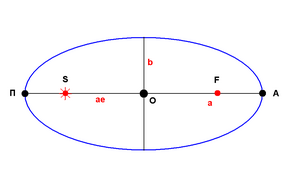
Видоизменим эту формулу, используя некоторые характеристики эллипса:

SO = a e, П = ПS = a (1 - e) - перигелийное расстояние,
A = AS = a (1 + e) - афелийное расстояние.

Преобразуем правую часть полученного третьего закона Кеплера и поэтому:

(a1 / a2)3 [{1 - e12} / {1 - e22}] = (a1 / a2) [{a1(1 + e1)} / {a2(1 + e2)}] [{a1 (1 - e1)} / {a2 (1 - e2)}] = (a1 / a2) (A1 / A2) (П1 / П2) .

Окончательно имеем:

(T1 / T2)2 [{Mc + m1} / {Mc + m2}] = (a1 / a2)3 [{1 - e12} / {1 - e22}] = (a1 / a2) (A1 / A2) (П1 / П2) .

Третий закон Кеплера на:

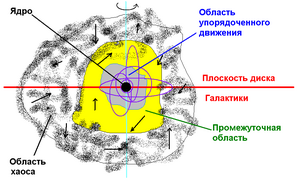
Хаос → порядок[править | править код]

Наша галактика - Млечный Путь
Начальная глобула
Глобулы в космосе (темные области)
Начало образования Солнечной системы

Активность ядра Галактики привела к тому, что в результате выброса вещества из ядра в окружающее пространство образовались сгущения этого вещества, сформировавшие спиральные рукава.

Определимся вначале относительно начальных условий образования Солнечной системы:

  • расстояние от центра Галактики - 30000 световых лет, скорость вращения вокруг ядра Галактики - 240 км/с, период обращения - 180 млн. лет;
  • состав - в основном атомарно-молекулярный водород и пыль;

Так как в глобуле газопылевое вещество находится в хаотическом движении, то на начальной стадии образования Солнечной системы ядра глобулы нет. Вместо ядра (= ЦМ) нужно рассматривать просто геометрический центр О глобулы. Если форма глобулы близка к сферической, то О ≈ ЦМ вещества глобулы. Пусть vср - средняя скорость хаотического движения газопылевых частиц. Температура T глобулы с течением времени увеличивается вследствие падающего на нее со всех сторон электромагнитного излучения и гравитационного сжатия (T ≠ 0). В результате хаотического движения вещества в глобуле образовываются ионизированный, атомарный и молекулярный водород. Так как плотность газопылевого вещества очень мала, то его можно рассматривать как идеальный газ и применять соответствующие уравнения для идеального газа.

Кроме слабых электромагнитных сил, на частицы вещества глобулы действуют гравитационные силы. Согласно ранее выведенному соотношению vгр ≈ 318 c, процесс сжатия происходит именно за счет гравитационных сил. Если, например, центральное ядро начнет увеличиваться ( по массе), то вещество глобулы быстрее будет реагировать с помощью гравитационного взаимодействия, нежели электромагнитного, т.е. будет притягиваться гравитационными силами к центру глобулы.

На прямой AC (≈ радиус глобулы) отмечены точки A, B и C. ↑R - равнодействующая гравитационная сила, действующая на частицу со стороны массы глобулы правее перпендикуляров к AC (в точках A, B, C) и направленная к точке C. ↑R' - равнодействующая гравитационная сила, действующая на частицу со стороны массы глобулы левее перпендикуляров к AC (в точках A, B, C) и направленная к точке A. Эти равнодействующие меняются в зависимости от того, какая масса вещества находится правее и левее перпендикуляров к AC. Вследствие различия этих равнодействующих гравитационных сил ↑R и ↑R' будет создаваться неравномерная плотность вещества глобулы. Наибольшее сжатие будет вблизи точки C и на внешней границе (вблизи точки A).

Предположим, что для газопылевого вещества глобулы абсолютная температура T = 10 K, масса частиц (атомарный водород) m = 10−27 кг. Тогда по формуле для идеального газа:

vср = (3 k T / m)1/2 ≈ 300 м/с .

Масса ядра M = 0 и по формуле получаем:

vвр = (γ M / R)1/2 = 0 ,

где vвр - скорость вращения (орбитальная скорость). Можно написать, что

vср >> vвр .

Так как вещество глобулы - идеальный газ, то vср - средняя скорость частиц идеального газа.

С течением времени происходит увеличение сжатия глобулы и образуется центральное ядро; увеличивается угловая скорость вращения ω и, соответственно, возрастает гравитационная сила притяжения частиц к ядру. При сжатии происходит также сплющивание глобулы вдоль оси вращения.

Для вращения глобулы вокруг своей оси справедлив кеплеровский закон:

vвр = (γ M / R)1/2 ,

где γ - постоянная всемирного тяготения, M - масса ядра глобулы, R - расстояние от ядра до рассматриваемой частицы. На этом этапе эволюции vвр глобулы необходимо считать функцией от переменных M и R. Поэтому в дальнейшей эволюции глобулы наступит равенство (при увеличении M):

vср = vвр ,

т.е. внутри глобулы возникает промежуточная область - хаоса и упорядоченного движения частиц. Вблизи ядра глобулы, где vвр = vорб > vср, образуется область упорядоченного движения (орбиты: окружность, эллипс и т.д.). Поэтому условие равенства скоростей - vср = vвр - можно рассматривать как основное условие для перехода от хаоса к упорядоченному движению.

Необходимо также отметить, что если бы глобула вращалась как твердое тело (vвр = ω R), то создание упорядоченных орбит шло бы от периферии к центру глобулы. Для кеплеровского закона (vвр = (γ M / R)1/2 ) упорядочение орбит идет от центра к периферии и может иметь место случай, когда после создания протосолнца на периферии глобулы останется область хаоса. Предполагая, что R глобулы, образовавшей Солнце, ≈10000 а.е. и Mc = 2×1030 кг, получаем по

vвр = (γ Mc / R)1/2 ≈100 м/с .

Так как vвр < vср (100 м/с < 300 м/с), то на периферии Солнечной системы есть область хаоса. Это справедливо и в случае максимального значения Rгл ~ 35000 а.е.

Итак, основной вывод можно рассмотреть таким образом:

  • ⇓ сжатие вещества электромагнитными и гравитационными силами + вращение
  • ⇓ создание центра масс (ЦМ) в виде массы ядра M
  • ⇓ увеличение M
  • ⇓ увеличение гравитационной силы взаимодействия между M и частицей массой m
  • ⇓ согласно (m vвр2) / R = (γ M m) / R2 увеличение vвр при R = const
  • ⇓ условие vвр > vср
  • ⇓ упорядочение орбит.

Несколько небольших добавлений к вышенаписанному процессу:

  • полная энергия падающих частиц на Mяд, превращаетcя, в основном, в гравитационную энергию , и эта энергия идет на разгон частиц до скорости vвр = (γ M / R)1/2 ;
  • в конечном итоге можно также утверждать, что вращение глобулы с угловой скоростью ω в какой-то мере ускоряет процесс сгущения центральной части - ядра глобулы, и одновременно ускоряет процесс упорядочения орбит частиц;
  • следует также добавить, что при упорядочении орбит происходят процессы образования и распада сгущений газопылевого вещества в разных областях глобулы.

Страница: 0 , 1 , 2 , 3 , 4 , 5 ,6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15 , 16 , 17 , 18

Примечания[править | править код]

См. также[править | править код]

Ссылки[править | править код]


Литература[править | править код]

Источник — https://traditio.wiki/w/index.php?title=Комплекс_%22Хеопс-Хефрен-Микерин%22%3D%22Атом_водорода%229&oldid=853778