Комплекс "Хеопс-Хефрен-Микерин"="Атом водорода"7
| Первоначальные исследования Этот раздел статьи является первичным источником части изложенной в нём информации, содержа первоначальные (или ранее не известные широкому кругу читателей) исследования. |
Семейство формул для аномального магнитного момента электрона и "призрак" электрона[править | править код]
При выводе формулы для аномального магнитного момента электрона (АММЭ) учитываются некоторые геометрические и физические характеристики атома водорода. Поэтому эти два варианта рассматриваются отдельно.
Геометрический аспект[править | править код]
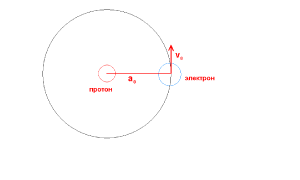
Рассмотрим движение точечного электрона на первой боровской орбите. Магнитный момент точечного электрона вычисляется (по определению) с помощью формулы
- μ0 = e v0 a0 ,
где e - электрический заряд электрона и e = const, v0 - скорость электрона, a0 - первый боровский радиус электрона и v0, a0 = const.Поэтому и μ0 = e v0 a0 = μБ - есть величина постоянная (магнетон Бора). Это в простейшем (идеальном) случае.
На самом деле электрон движется по другой орбите, и само понятие "электрон" усложняется. Вследствие этого и магнитный момент будет отличаться от μБ. Назовем этот магнитный момент аномальным и займемся в дальнейшем его вычислением. При этом предполагаем, что электрический заряд точечного электрона не меняется, а меняются только ↑v и ↑r, где v и r - истинные значения скорости и радиуса-вектора электрона:
- μан = e v r .
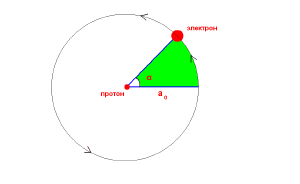
Произведение v r можно представить по-другому, используя второй закон Кеплера:
- v r = 2 S / t ,
где S - площадь, описываемая радиусом-вектором r электрона за время t. Будем рассматривать это соотношение за время T0 (период обращения электрона вокруг ядра).
Согласно изложенному ранее (1, 2) сложное движение точечного электрона в атоме водорода:
- движение точечного электрона в электрическом поле неподвижного протона - окружность радиуса a0 (первая боровская орбита);
- движение точечного электрона в магнитном поле движущегося протона - окружность (предельная электронная орбита);
заменяем на более простое, приблизительно равноценное:
- движение точечного электрона в электрическом поле неподвижного протона + смещение точечного электрона на угол α (постоянная тонкой структуры - учет магнитного поля движущегося протона).
Значит, за один полный оборот точечного электрона вокруг ядра (T0 - период обращения) в электрическом поле неподвижного протона точечный электрон дополнительно смещается в том же направлении на угол α или на расстояние, равное радиусу предельной электронной орбиты.
Усложнение орбиты точечного электрона состоит в следующем:
- смещение точечного электрона на угол α - движение по эллипсу;
- замена точечного электрона на протяженный электрон.
При движении точечного электрона по эллипсу происходит смещение периядра (ближайшая точка электронной орбиты к ядру) точечного электрона. Если движение точечного электрона происходит по окружности (эллипсу), то лучше всего словосочетание "смещение точечного электрона по орбите" заменить на "смещение электрона".
Второй закон Кеплера к боровскому варианту (идеальный случай) атома водорода дает следующее:
- μБ = e v0 a0 = e (2 S0 / T0).
В случае смещения (более естественный случай) будет:
- μан = e v r = e (2 S / T0).
Тогда
- μан / μБ = S / S0 или μан = μБ (S / S0).
Значит, аномальный магнитный момент электрона можно вычислять через магнетон Бора и отношение площадей, описываемых радиусом-вектором точечного электрона в усложненном варианте и в боровском случае. В случае боровской орбиты S0 = π a02. Поэтому
- μан = μБ (S / π a02) .
В дальнейшем для простоты записи примем
- μан / μБ = S / π a02 .
Если при наличии магнитного поля протона происходит смещение радиуса-вектора точечного электрона на угол α, то это означает, что радиус-вектор описывает за один полный оборот относительно электрического поля протона площадь S0 = π a02 и дополнительную площадь в форме сектора с центральным углом α. Площадь сектора
- Sсек = (α/2) a02.
Поэтому
- S = Sокр + Sсек = π a02 + (α/2) a02 .
Тогда
- μан / μБ = [π a0 + α (a02 / 2)] / π a02 = 1 + (α / 2 π) .
- μан / μБ = 1 + (α / 2 π) .
Мы пришли в первом приближении к формуле Швингера.
В Солнечной системе эксцентриситеты планетных орбит считаются заданными, поэтому поступим аналогично и для электрона в атоме водорода. Для этого будем переходить к более реальному атому водорода.
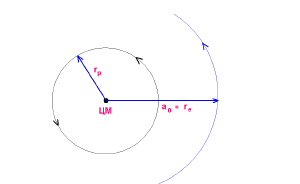
На самом деле протон и электрон двигаются по своим орбитам (окружностям) вокруг центра масс (ЦМ). Следовательно, периоды обращения протона и электрона (относительно ЦМ) одинаковы и равны:
- Tp = Te = T0
или, выражая через длины окружностей и скорости, получаем:
- Lp / vp = Le / ve .
Далее:
- Lp / Le = vp / ve ,
где vp и ve - скорости протона и электрона на орбитах. Продолжая дальше, имеем:
- Lp / Le = 2 π rp / 2 π re = vp / ve или vp / ve = rp / re ,
где re - радиус орбиты точечного электрона, rp - радиус орбиты протона.
Из классической механики известно, что для двух взаимодействующих тел отношение модулей ускорений равно обратному отношению их масс:
- ap / ae = me / mp ,
где ap и ae - ускорения протона и электрона на орбитах, mp и me - массы протона и электрона. Объединяя, получаем:
- rp / re = vp / ve и ap / ae = me / mp.
Для центростремительных ускорений имеем:
- ap = vp2 / rp и ae = ve2 / re .
Откуда:
- ap / ae = (vp2 / ve2) (re / rp) → me / mp = (rp / re)2 (re / rp) = rp / re .
Видоизменение этой формулы:
- me / mp = rp / re или me / mp = rp / a0 → rp = (me / mp) a0.
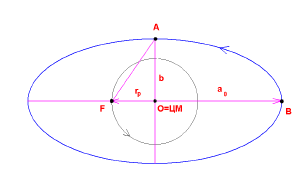
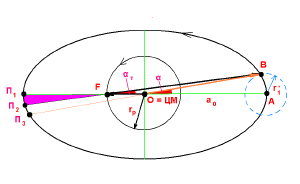
Согласно первому закону Кеплера рассматриваем движение точечного электрона по эллипсу, в котором a0 (первый боровский радиус) - большая полуось, ЦМ в центре эллипса и протон в левом фокусе F. Малая полуось эллипса может быть вычислена. На рисунке масштаб не соблюден.
OB = a0 - большая полуось, OA = b - малая полуось, OF = rp - фокусное расстояние, O = ЦМ - центр масс. AF = a0 и поэтому
- b = (a02 - rp2)1/2 .
Подставляем вместо rp полученное выражение
- b = [a02 - (me/mp)2 a02]1/2 = a0 [1 - (me/mp)2]1/2 .
Для эллипса связь между полуосями точно такая же: b = a0 (1 - e2)1/2, где e - эксцентриситет эллипса. Следовательно, эксцентриситет электронной орбиты e = me / mp .
Ранее мы выяснили, что α (постоянная тонкой структуры) - это угол при вершине в центре ядра (протона), а дуга (точнее хорда), опирающаяся на α - радиус r1' (предельная электронная орбита). Радиус-вектор электрона соединяет центры протона и электрона.
В случае эллиптической электронной орбиты дело усложняется. Протон в точке F - левый фокус эллиптической орбиты электрона, электрон в точке B. П2 - положение периядра при смещении электрона. П1 и П3 - положения периядра при несмещенном электроне и положениях протона в точках O и F. a0 = OA, rp = OF. Кроме радиуса-вектора электрона - ↑FB, необходимо рассматривать радиус-вектор протона - ↑OF. Угол α заменяется другим углом αт. Поэтому из условия
α a0 = αт (rp + a0) = r1' (предельная электронная орбита = const)
можем определить угол αт:
- αт = α a0 / (rp + a0) = α a0 / [(me/mp)a0 + a0] = α [1 / {1 + (me/mp)}].
В ОТО Эйнштейн рассматривал смещение перигелия орбиты планеты (Меркурий). Поэтому и мы рассмотрим смещение периядра электрона на первой боровской орбите. Радиус-вектор электрона FB будет ометывать площадь эллипса, т.е. Sэлл. Площадь эллипса:
- Sэлл = π a0 b = π a02 [1 - (me/mp)2]1/2.
Вместо сектора смещения S = α a02 / 2 = S(AOB) = S(П1ОП3) (боровский вариант) будет сектор смещения:
- S(FП1П2) = (αт/2)(a0 - rp)2 = (α/2)[1 / {1 + (me/mp)}] [1 - (me/mp)]2 a02.
К этим площадям добавится площадь, ометываемая радиусом-вектором протона:
- Sp = π rp2 = π (me / mp)2 a02.
Радиус-вектор протона ≈ радиус-вектор "призрака" электрона (см. далее) и поэтому Sp ≈ Se', где Se' - площадь, ометываемая радиусом-вектором "призрака" электрона. Учитывая, что электрон протяженный (re - классический радиус электрона) и поэтому для протяженного электрона - Se.
Принимая все вышеизложенное, мы можем тогда написать:
- μан / μБ = [Sэлл / π a02] + [S(FП1П2) / π a02] + [Sp / π a02] + [Se / π a02] .
Следует отметить, что смещение периядра происходит в том же направлении, в каком направлении движется электрон на орбите.
Для того, чтобы вычислить Se / π a02, необходимо сделать небольшое отступление.
Введение центра масс означает, что гравитационные поля протона и электрона также влияют на поведение системы протон-электрон. Учтем в дальнейших расчетах скорости распространения электромагнитных и гравитационных волн - c и vгр, причем vгр >> c. Далее примем во внимание классический радиус электрона re = α2 a0.
Взаимодействие между электрическими зарядами "+" и "-" осуществляется путем излучения и поглощения виртуальных фотонов. Этому случаю соответствует третий вариант интерпретации a0 = ħ / α c me (см. далее). По аналогии примем, что и гравитационное взаимодействие между массами осуществляется виртуальными гравитонами.
Ранее было получено выражение для первого боровского радиуса электрона в атоме водорода:
- a0 = ħ / α c me,
где α c = v0 - скорость электрона на первой боровской орбите, me - масса электрона. Тогда
- a0 = ħ / me v0.
Согласно гипотезе Луи де Бройля (1924 г.), если электрон имеет энергию E и импульс p, то с электроном связана волна, частота которой ν = E / h и длина волны
- λe = h / p = h / me v.
Эта волна получила название волны де Бройля. О волнах де Бройля часто говорят как о волнах вероятности.
Поэтому, объединяя первый боровский радиус и волну де Бройля, получаем:
- a0 = ħ / me v0 и λe = ħ / me v = 2 π (ħ / me v) ===> a0 = h / me v0 и λe / 2 π = ħ / me v.
При v = v0:
- λe = 2 π a0 ,
т.е. боровский радиус a0 можно рассматривать как длину волны виртуального фотона.
Итак, движение электрона в атоме водорода на первой боровской орбите можно интерпретировать как:
- 1) движение точечного электрона на расстоянии a0 от ядра со скоростью v0 = α c;
- 2) перемещение волны де Бройля с длиной волны λe = 2 π a0 и скоростью v0 = α c.
Но есть и третий вариант:
- 3) a0 = ħ / (α me) c = ħ / m' c
или
m' = α me = ħ / c a0 - виртуальный фотон с длиной волны a0 и скоростью c.
Ранее было введено понятие "предельная электронная орбита" и получено уравнение Lм = 2 π r1'. Предельная электронная орбита - орбита, по которой двигался бы электрон со скоростью света.
С другой стороны, объединяя 1) и 2) интерпретации движения электрона, можно делать вывод, что выражение Lм = 2 π r1' следует понимать как "волна де Бройля с длиной волны λe' = Lм = 2 π r1' и скоростью vм = α2 c".
Следовательно, надо различать волну де Бройля для электрона, двигающегося в электрическом поле протона от волны де Бройля для электрона, двигающегося в магнитном поле протона. Видимо, следует рассматривать общую волну де Бройля для электрона:
- λe = λe(ЭП,МП).
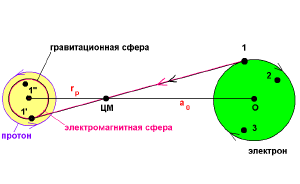
Представим, что протон и электрон "остановились" бы в своих орбитальных движениях относительно центра масс, но "вращались" бы вокруг своих осей. Тогда каждую точку (1,2,...) электрона можно рассматривать как источник виртуальных фотонов и гравитонов. "Вращения" протона и электрона произвольные. Размеры на рисунках не соблюдены.
Принимая во внимание, что расстояния (a0, rp) и длины волн (λe, λp) связаны с центром масс, рассмотрим электромагнитное и гравитационное взаимодействия, осуществляемые через через центр масс. т.е. потоки виртуальных фотонов и гравитонов проходят через центр масс.
Ввиду разных скоростей c и vгр, электромагнитные и гравитационные волны (виртуальные фотоны и гравитоны), испущенные одновременно из точки 1 на (внутри) электроне, дойдут до протона за разное время. Виртуальные гравитоны попадают в точку 1', а виртуальные фотоны - в другую точку 1". Все точечные источники на (внутри) электроне (= материальные точки), излучая виртуальные фотоны и гравитоны, будут образовывать 2 сферы - электромагнитную и гравитационную. В этом случае центры этих сфер совпадают. Отсюда следует вывод, что необходимо рассматривать и 2 радиуса-вектора. Первый радиус-вектор соединяет электромагнитную сферу с точкой 1; второй радиус-вектор соединяет гравитационную сферу с точкой 1. Аналогично и для всех других точек на сферах и электроне. Таким образом вводятся понятия электромагнитного ↑rэл и гравитационного ↑rгр радиусов-векторов для электрона.
Аномальный магнитный момент электрона на:
- http://www.scientific.ru/spark/muonanomaly.html
- http://ufn.ru/ru/articles/1949/11/b/
- http://lib.mexmat.ru/books/7057
- http://ru.wikipedia.org/wiki/Электрон
- http://revolution.allbest.ru/physics/00048992_0.html
- http://physics.vniim.ru/webco2/qed/m_enc/QED_and_FPC.html
- http://www.astronet.ru/db/msg/1172494
- http://heritage.sai.msu.ru/ucheb/Zemcov/Part_3_Hydrogen/Chapter_19/chapter_19.htm
- http://web.archive.org/web/20050322225848/http://www.cultinfo.ru/fulltext/1/001/008/060/306.htm
- http://femto.com.ua/articles/part_1/0151.html
Электрон на:
- http://ru.wikipedia.org/wiki/Электрон
- http://nts.sci-lib.com/article0005707.html
- http://nuclphys.sinp.msu.ru/spargalka/a35.htm
- http://physics.kgsu.ru/astronomia/NV/Elektron.htm
- http://www.diclib.com/cgi-bin/d1.cgi?l=ru&base=bse&page=showid&id=84427
- http://www.alhimik.ru/stroenie/gl_4.html
- http://www.physical-congress.spb.ru/russian/kozhev/Kozhev.asp
Страница: 0 , 1 , 2 , 3 , 4 , 5 ,6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15 , 16 , 17 , 18
Примечания[править | править код]
См. также[править | править код]
Ссылки[править | править код]
Литература[править | править код]
- Физический энциклопедический словарь. М."Советская энциклопедия". 1983
- Л.Д.Ландау, Е.М.Лифшиц. Теоретическая физика. //Теория поля.Т.II.М."Наука". 1988
- В.Б.Берестецкий, Е.М.Лифшиц, Л.П.Питаевский. Теоретическая физика//Квантовая электродинамика.Т.IV.М."Наука". 1989
- Ю.А.Храмов. Физики//Биографический справочник.М."Наука". 1983
- О.П.Спиридонов. Универсальные физические постоянные.М."Просвещение". 1984
- Л.Р.Стоцкий. Физические величины и их единицы.М."Просвещение".1984
- Дж.Нарликар. Гравитация без формул/перев. с англ./.М."Мир". 1985
- В.Л.Гинзбург. О физике и астрофизике.М."Наука". 1985
- В.Чолаков. Нобелевские премии//Ученые и открытия/перев. с болг./.М."Мир". 1987
- В.П.Цесевич. Что и как наблюдать на небе.М."Наука". 1984
- И.С.Шкловский. Вселенная.Жизнь.Разум.М."Наука". 1987
- Б.А.Воронцов-Вельяминов. Очерки о Вселенной.М."Наука". 1980
- Я.Б.Зельдович, И.М.Яглом. Высшая математика//Для начинающих физиков и техников.М."Наука". 1982
- Г. Корн, Т. Корн. Справочник по математике//Для научных работников и инженеров/перев. с амер./.М."Наука". 1984