Комплекс "Хеопс-Хефрен-Микерин"="Атом водорода"16

Материал из свободной русской энциклопедии «Традиция»
Перейти к навигации Перейти к поиску
Periss icon.png Первоначальные исследования
Этот раздел статьи является первичным источником части изложенной в нём информации, содержа первоначальные (или ранее не известные широкому кругу читателей) исследования.

[править | править код]

В пределах формулы α = e2 / 4 π ε0 ħ c введем закон сохранения количества постоянных. Классификацию постоянных в формуле для α можно делать разными способами по принадлежности к разным множествам:

I а) 2, 4 - рациональные числа (2);
  б) π - иррациональное число (1);
  в) e, ε0, ħ, c, α - фундаментальные физические постоянные (5);
II а) 2, 4 - рациональные числа (2);
  б) e, ε0, ħ, c, α , π - иррациональные числа (6).

Первую классификацию - (2-1-5) - возьмем в качестве стороны основания (квадрат) второй пирамиды - 215.

Число 233 (сторона основания первой пирамиды) по чистой случайности "попало" в этот закон сохранения:

2 + 3 + 3 = 2 + 1 + 5 = 8 (const) .

Число π = 3,14 (без разделителя + 3 значащих цифры) по случайности "попало" в этот закон сохранения:

3 + 1 + 4 = 2 + 3 + 3 = 2 + 1 + 5 = 8 (const) .

Итак, вторая правильная усеченная 4-угольная пирамида готова (высота 136, сторона нижнего основания 215).

В формуле для α число 4 можно записать как:

4 = 22 = 2 × 2 = 2 + 2 .

Тогда в формуле для α будет фигурировать только целое число 2. Поэтому вторую классификацию нужно брать не в виде 2-6, а в виде 6-2, так как:

137 / 62 = 2,20... и 136,6 / 62 = 2,20... (1-3 значащие цифры),

многократно дублируя 2. Следовательно, классификацию 6-2 берем в качестве связи с третьей пирамидой, а именно - высота третьей пирамиды = 62.

И, окончательно, связываем все стороны оснований пирамид соотношением:

233 / 215 = 1,08... или = 108 (1-3 значащие цифры + психология).

В итоге получаем кольцевую связь всех трех правильных пирамид.

Пирамидионы[править | править код]

Ошибка создания миниатюры: Файл не найден
Рис. 30-3. Примерный (без соблюдения пропорций) вид и основные размеры первой пирамиды

Верхушечная пирамидка - пирамидион - правильная 4-угольная пирамида над основной пирамидой.

Согласно формуле π = 105 / 137,03...×232,28... , основание степени 105 (т.е. 10) должно равняться стороне верхнего основания первой пирамиды (т.е 10), а высота пирамидиона = показателю степени (т.е. 5). Если площадь верхней площадки - площадь квадрата, то площадь квадрата = 102 = 100 . С другой стороны 10 ≈ π2 (небольшая точность) или π ≈ (10)1/2 = 3,1415... . Поэтому для расчетного варианта принимаем:

(10)1/2 = π .

Угол наклона боковой грани β первой усеченной правильной 4-угольной пирамиды:

tg β = 137 / (233 / 2 - 10 / 2) = 137 / (116,5 - 5) = 137 / 111,5 = 1,228699 .
β = arctg 1,228699 = 50° 51′ 32″ (от автора: современные единицы измерения плоских углов).

Пирамидион первой пирамиды имеет грани, которые наклонены под углом β' к плоскости основания:

tg β ' = 5 / (10 / 2) = 5 / 5 = 1 .
β ' = arctg 1 = 45° (от автора: современные единицы измерения плоских углов).

Этот угол β ' = 45° намекает на прямоугольный треугольник.

Общая высота первой пирамиды: 137 + 5 = 142.

Частная формула 1. С учетом 10 = π2 из первоначальной формулы получаем:

137,03... × 232,28... = 105 / π = (π2)5 / π = π10 / π = π9 .

Откуда (небольшая точность):

π = (137,03... × 232,28...)1/9 .

Частная формула 2. Кольцевая связь всех трех пирамид:

233 / 215 = 1,08 или 108 (1-3 значащие цифры + психология).

Это же соотношение, выраженное математически:

233 / 215 = 1,08 = 108 / 102 .

Откуда

102 = 108 × 215 / 233 .

Учитывая 10 = π2 , получаем:

π4 = 108 × 215 / 233 .

Или (небольшая точность)

π = (108 × 215 / 233)1/4 .

Пирамидион на: 

От автора: в данной статье использованы некоторые цитаты из книги - Бабанин Владимир "Тайны великих пирамид". Санкт-Петербург, 1998, 509 стр.

Стр. 50: В Египте знали и уважали Геродота. Когда он в V веке до н.э. прибыл на Нил, чтобы увидеть все своими глазами и услышать своими ушами, жрецы многое ему показали и о многом рассказали. В том числе и о пирамидах. А Геродот добросовестно и скрупулезно все запоминал и записывал, чтобы потом рассказать всем об этом в своей "Истории". Так мы узнали такую интересную подробность: оказывается, в пирамиде площадь боковой грани равна площади квадрата, у которого сторона равна высоте пирамиды. Правда, жрецы не уточнили, о каких пирамидах шла речь: с остроконечной вершиной или вершиной усеченной. Исследователи, естественно, неоднократно проверяли потом сообщение жрецов на "живых" пирамидах и ... были разочарованы: не получалось равенства площадей двух разных фигур...

Далее следуют рассуждения от лица автора, а не от Я.

Рис. 30-4. Правильная 4-угольная пирамида
  • a - основание правильной 4-угольной пирамиды;
  • h - высота правильной 4-угольной пирамиды;
  • x - апофема боковой грани правильной 4-угольной пирамиды;
  • в основании правильной 4-угольной пирамиды квадрат;
  • 0 - центр квадрата основания.

Утверждение жрецов:

a x / 2 = h2 .

Теорема Пифагора:

h2 + a2 / 4 = x2 .

Тогда из теоремы Пифагора:

h2 = x2 - a2 / 4 .

Подставим в первое уравнение:

a x / 2 = x2 - a2 / 4 .

Или

x2 - a x / 2 - a2 / 4 = 0 .

Умножим уравнение на 4:

4 x2 - 2 a x - a2 = 0 .

Решаем квадратное уравнение:

x1,2 = [2 a ± (4 a2 + 16 a2)1/2] / 8 = [2 a ± (20 a2)1/2] / 8 = [2 a ± 2 a (5)1/2] / 8 = [a ± a(5)1/2] / 4 = a (1 ± 51/2) / 4 .

Используем положительный корень уравнения:

x1 = x = a (1 + 51/2) / 4 .

Подставим в высказывание жрецов:

(a / 2) [a (1 + 51/2) / 4] = h2 .

Или

h2 = (a2 / 8) (1 + 51/2) .

Окончательно:

h = [(a2 / 8) (1 + 51/2)]1/2 = (a / 2) [(1 + 51/2) / 2]1/2 .

Найдем тангенс угла наклона боковой грани (треугольник) к плоскости основания (квадрат):

tg β = h / (a / 2) = [(1 + 51/2) / 2]1/2 = 1,27201964...
(1 + 51/2) / 2 = 1,618033... = φ - "золотое сечение" .

Тогда

tg β = φ1/2 = (1,618033...)1/2 = 1,27201964...

и

β = arctg 1,27201964 = 51° 49′ 38″ - "золотой угол".

Второй острый угол в прямоугольном треугольнике:

90° - 51° 49′ 38″ = 38° 10′ 22″ .

"Золотое сечение" φ = 1,61 (1-3 значащие цифры) тоже случайно(?) "вошло" в закон сохранения постоянных:

1 + 6 + 1 = 8 (const).

Уравнение

4 x2 - 2 a x - a2 = 0

имеет и второй корень:

x2 = x = a [(1 - 51/2) / 2] .

Тогда

(a / 2) a [(1 - 51/2) / 4] = h2 .
h2 = (a2 / 8) (1 - 51/2) .

Или

h = [(a2 / 8) (1 - 51/2)]1/2 = (a / 2) [(1 - 51/2) / 2]1/2 .

Тогда имеем:

tg β = h / (a / 2) = [(1 - 51/2) / 2]1/2 = (- 0,61803398...)1/2 = (0,61803398...)1/2×(- 1)1/2 = 0,786151... (- 1)1/2 = 0,786151... × ι ,

где ι = (- 1)1/2 - мнимая единица.

Без учета ι = (- 1)1/2 :

tg β = 0,786151...

и

β = arctg 0,786151 = 38° 10′ 22″ .

Или (с учетом ι = (- 1)1/2 ):

β = 38° 10′ 22″ × ι - мнимый угол.

Но угол 38° 10′ 22″ (без × ι) (действительный угол) действительно есть в прямоугольном треугольнике с "золотым углом" 51° 49′ 38″ и расположен в вершине пирамиды. Логично угол 38° 10′ 22″ назвать "мнимым золотым углом".

Ранее (движение точечного электрона в электрическом поле протона) было выведено значение первой боровской орбиты:

a0 = ħ2 / k' e2 m = ħ / α m c = 5,2917706 × 10- 11 м.

Аналогично ранее (движение точечного электрона в магнитном поле протона, движущегося относительно центра масс) было получено выражение для предельной электронной орбиты (= смещение электрона):

R = α a0.

Также была получена формула для классического радиуса электрона:

re = α2 a0 или re = α R .
Файл:Zolotoe setshenie.jpg
Рис.30-5. Золотое сечение отрезка
Рис. 30-6. Прямоугольный треугольник и золотое сечение
Рис. 30-7. Геометрия атома водорода

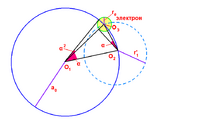
Тогда

R = α a0 ==> a0 / R = 1 / α = 137 (const);
re = α R ==> R / re = 1 / α = 137 (const) .

Или

a0 / R = R / re = 1 / α ; R / a0 = re / R = α .

Для золотого сечения отрезка AB точкой C (отрезки a и b):

(a + b) / a = a / b = φ = 1,61 .

Если

  • a = h (общая высота второй пирамиды);
  • b = a / 2 (половина нижнего основания второй пирамиды),

то

(h + a / 2) / h = h / (a / 2) = φ = (1 + 51/2) / 2 .

Во второй пирамиде (и в остальных) расположение этих h и a/2 иное. Они образуют прямоугольный треугольник и тогда (+ пример со жрецами):

h / (a / 2) = tg β = (φ)1/2 = [(1 + 51/2) / 2]1/2 .

Из сравнения этих двух пропорций следует, что

R / a0 = re / R = α

можно назвать "золотым сечением" атома водорода.

Так как постоянная тонкой структуры α = 7,29 × 10−3 - малый угол при вершине (ядро атома водорода) для предельной электронной орбиты, то и "золотое сечение" φ = 1,61 необходимо рассматривать относительно углов. Эти два "золотых сечения" можно написать в виде:

2 h / a φ1/2 = 1 и α a0 / R = α R / re = 1 .

Или

2 h / a φ1/2 = α a0 / R = α R / re ≡ 1 .

Геометрия этих соотношений - для пирамиды и атома водорода - схожа: ≈ прямоугольные треугольники. "Золотое сечение" в треугольнике ("золотой угол" ~ 52°) связано неявно с "золотым сечением" атома водорода (угол α - постоянная тонкой структуры). 

Далее рассуждения от имени Я.
Рис. 30-8. Примерный (без соблюдения пропорций) вид и основные размеры второй пирамиды

Применяем во второй пирамиде "золотой угол" 51° 49′ 38″ ("золотое сечение") для определения общей высоты 2-ой пирамиды H:

H / (a / 2) = tg β = φ1/2 ,

где a - сторона нижнего основания.

Тогда

H = (a / 2) φ1/2 = (215 / 2) × 1,272 = 136,740 .

Высота 2-ого пирамидиона:

H - 136= 0,740 .

Для 2-ого пирамидиона:

0,740 / (b / 2) = tg β = φ1/2 ,

где b - сторона основания пирамидиона.

b / 2 = 0,740 / φ1/2 .

Сторона основания пирамидиона:

b = 2 × 0,740 / φ1/2 = 1,163 .
От автора: определите самостоятельно размеры 3-его пирамидиона и угол наклона боковой грани 3-ей основной пирамиды.

Золотое сечение на:

Страница: 0 , 1 , 2 , 3 , 4 , 5 ,6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15 , 16 , 17 , 18

Примечания[править | править код]

См. также[править | править код]

Ссылки[править | править код]

Литература[править | править код]

Источник — https://traditio.wiki/w/index.php?title=Комплекс_%22Хеопс-Хефрен-Микерин%22%3D%22Атом_водорода%2216&oldid=853636