Комплекс "Хеопс-Хефрен-Микерин"="Атом водорода"5

Материал из свободной русской энциклопедии «Традиция»
Перейти к навигации Перейти к поиску
Periss icon.png Первоначальные исследования
Этот раздел статьи является первичным источником части изложенной в нём информации, содержа первоначальные (или ранее не известные широкому кругу читателей) исследования.

Движение в центрально-симметричном гравитационном поле[править | править код]

Л.Д.Ландау, Е.М.Лифшиц.Теория поля.1983

Рассмотрим движение частицы в центрально-симметричном гравитационном поле. Как и во всяком центральном поле, движение будет происходить в одной "плоскости", проходящей через центр поля; выберем эту плоскость в качестве плоскости θ = π/2.

Для определения траектории частицы воспользуемся уравнением уравнением Гамильтона-Якоби

gik(∂S/∂xi)(∂S/∂xk) - mc2 = 0,

где m - масса частицы (массу же центрального тела обозначим здесь как m'), c - скорость света. С метрическим тензором

ds2 = (1 - rg/r)c2dt2 - r2(sin2θ dφ2 + dθ2) - dr2/(1 - rg/r)

это уравнение принимает вид

(1 - rg/r)−1(∂S/c∂t)2 - (1 - rg/r)(∂S/∂r)2 - 1/r2(∂S/∂φ)2 - m2c2 = 0,

где rg = 2m'γ/c2 - гравитационный радиус центрального тела (Солнца).

По общим правилам решения уравнения Гамильтона-Якоби ищем S в виде

S = - E0t + Mφ + Sr(r)

с постоянной энергией E0 и моментом импульса M. Подставив S = - E0t + Mφ + Sr(r) в (1 - rg/r)−1(∂S/c∂t)2 - (1 - rg/r)(∂S/∂r)2 - 1/r2(∂S/∂φ)2 - m2c2 = 0, найдем производную dSr/dr и затем:

Sr = ∫[E02/c2(1 - rg/r)−2 - (m2c2 + M2/r2)(1 - rg/r)−1]1/2 dr.

Зависимость r = r(t) дается уравнением ∂S/∂E0 = const, откуда

ct = E0/mc2 ∫dr /(1 - rg/r)[(E0/mc2)2 - (1 + M2/m2c2r2)(1 - rg/r)]1/2.

Траектория же определяется уравнением ∂S/∂M = const, откуда

φ = ∫ M/r2 [E02/c2 - (m2c2 + M2/r2)(1 - rg/r)]−1/2 dr.

Этот интеграл приводится к эллиптическому.

Для движения планет в поле тяготения Солнца релятивистская теория приводит лишь к незначительным поправкам по сравнению с теорией Ньютона, поскольку скорости планет очень малы по сравнению со скоростью света. В уравнении траектории φ = ∫ M/r2 [E02/c2 - (m2c2 + M2/r2)(1 - rg/r)]−1/2 dr этому соответствует малость отношения rg/r (для Солнца rg/r = 3 км; для Земли rg/r = 0,9 см).

Для вычисления релитивистских поправок к траектории удобно исходить из выражения φ = ∫ M/r2 [E02/c2 - (m2c2 + M2/r2)(1 - rg/r)]−1/2 dr. радиальной части действия до его дифференцирования по M. Заменим переменную интегрирования согласно r(r - rg) = r'2, т.е. r - rg/2 ≈ r', в результате чего член с M2 под корнем примет вид M2/r'2. В остальных же членах производим разложение по степеням rg/r' и получаем с требуемой точностью:

Sr = ∫ [(2E'm + E'2/c2) + 1/r(2m2m'γ + 4E'mrg) - 1/r2(M2 - 3m2c2rg2/2)]1/2 dr,

где мы для краткости опустили штрих у r' и ввели нерелятивистскую энергию E' (без энергии покоя).

Поправочные члены в коэффициентах в первых двух членах под корнем отражаются только на не представляющем особого интереса изменении связи между энергией и моментом частицы и параметрами ее ньютоновской орбиты (эллипса). Изменение же коэффициента при 1/r2 приводит к более существенному эффекту - к систематическому (вековому) смещению перигелия орбиты.

Поскольку траектория определяется уравнением φ + ∂Sr/∂M = const, то изменение угла φ за время одного оборота планеты по орбите есть

Δφ = - (∂/∂M) ΔSr,

где ΔSr - соответствующее изменение Sr. Разлагая Sr по степеням малой поправки в коэффициент при 1/r2, получим:

ΔSr = ΔSr(0) - (3m2c2rg2/4M) (∂ΔSr(0)/∂M),

где ΔSr(0) соответствует движению по несмещающемуся замкнутому эллипсу. Дифференцируя это соотношение по M и учитывая, что

- ∂ΔSr(0)/∂M = Δφ(0) = 2π ,

найдем

Δφ = 2π + (3πm2c2rg2/2M2) = 2π + (6πγ2m2m'2/c2M2).
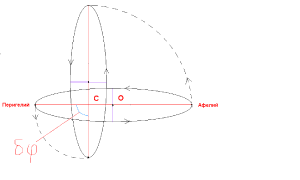
Смещение перигелия орбиты планеты δφ. Размеры и углы произвольные.

Второй член и представляет собой искомое угловое перемещение δφ ньютоновского эллипса за время одного оборота, т.е. смещение перигелия орбиты. Выражая его через длину большой полуоси a и эксцентриситет e с помощью известной формулы M2/γm'm2 = a(1 - e2), получим:

δφ = 6πγm'/c2a(1 - e2) = 6πγMc/c2a(1 - e2) при m' = Mc.

Численные значения смещения, определяемого этой формулой, для Меркурия и Земли равны соответственно 43,0" и 3,8" в сто лет.

От автора:

  • для читателей с недостаточной математической подготовкой принять во внимание только выведенную формулу для смещения перигелия орбиты планеты;
  • следует заметить, что δφ существует и тогда, когда e = 0, т.е. для круговой орбиты.

Движение в центрально-симметричном гравитационном поле на:

Смещение перигелия - номер планеты[править | править код]

Для определения номеров планет Венеры и Земли, включая остальные известные и неизвестные планеты, введем понятие - предельная гравитационная орбита планеты.

Чем ближе планета к Солнцу, тем больше ее орбитальная скорость и при этом остается справедливым второй закон Кеплера. Рассмотрим орбиты планет, которые появляются при v→c, где v - орбитальная скорость, c - скорость света. Вернемся снова к квантованию Солнечной системы:

vn rn = 2 n h',

где vn - орбитальная скорость n-ой планеты, rn - среднее расстояние n-ой планеты от Солнца, n = 0,1,2,... - номер гравитационной орбиты планеты (главное квантовое число для гравитационного поля), h' = 1,3859×1015 м2/с - гравитационная солнечная постоянная.

Для гравитационных орбит планет дополнительно получаем:

c rN' = 2 N h',

где rN' - среднее расстояние планеты от Солнца относительно предельной гравитационной орбиты, N = 0,1,2,... - номер гравитационной орбиты планеты относительно предельной гравитационной орбиты. При N = 1 получаем:

c r1' = 2 h'.

Откуда находим

r1' = 2h' / c = 9244 км - предельная гравитационная орбита для планет.

Объединяем:

Меркурий - v1r1 = 2 h',

предельная гравитационная орбита - cr1' = 2 h'

и получаем:

(v1 / c)(r1 / r1') = 1 или v1 / c = r1' / r1.

Одна и та же реальная орбита планеты должна иметь разные порядковые номера n и N. Поэтому rn = rN или

n2 r1 = N2 r1'.

Если n = 1, то r1 = N2r1' - для Меркурия. Откуда вытекает N = 79.

Следовательно, для произвольной планеты имеем:

N2 = n2 (rn / r1') = rn / r1'

и N можно определять по формуле:

N = (rn / r1')1/2 ,

где N - номер гравитационной орбиты планеты относительно предельной гравитационной орбиты.

Номера планет N для Солнечной системы относительно предельной гравитационной орбиты приведены ниже (таблица 5).

Таблица 5

Номер по порядку Планета N
1 Меркурий 79
2 Венера 107
3 Земля 126
4 Марс 157
5 Юпитер 290
6 Сатурн 393
7 Уран 558
8 Нептун 699
9 Плутон 800

Выведенное в общей теории относительности (ОТО) смещение перигелия орбиты планеты δφ применим в дальнейших расчетах.

δφ1 = 6 π γ Mc / c2 r1(1 - e12), n = 1 ,

где r1 и e1 - расстояние от Солнца до Меркурия и эксцентриситет орбиты Меркурия. Так как

γ Mc = v12 r1 , то 6 π γ Mc / c2 = 6 π v12 r1 / c2.

Далее:

6 π γ Mc / c2 r1 = 6 π v12 / c2 ===> 6 π γ Mc / c2 r1(1 - e12) = [6 π / (1 - e12)](v1 / c)2.

Учитывая, что

v1 / c = r1' / r1

получаем:

6 π γ Mc / c2 r1(1 - e12) = [6 π / (1 - e12)](r1' / r1)2 = [6 π / (1 - e12)](r1' / N12 r1')2 = [6 π / (1 - e12)](1 / N14).

Следовательно, для первой планеты - Меркурия

δφ1 = 6 π γ Mc / c2 r1(1 - e12) = [6 π / (1 - e12)](1 / N14).

Поэтому из этой формулы получаем:

N1 = [6 π / (1 - e12)δφ1]1/4 ≈ [6 π / δφ1]1/4.

Таким образом, зная смещение перигелия орбиты планеты δφ, можно определять номер гравитационной орбиты N и наоборот.

Ранее были рассмотрены случаи [(4,6,8),(3,6,8) и "Вулкан - ..."] для объяснения аномалий в Солнечной системе - астроинженерная деятельность ВЦ. Этот пункт дает более естественное объяснение строения Солнечной системы.

Смещение перигелия планеты на:

Скорость гравитационных волн (взаимодействий)[править | править код]

Запишем значение скорости планеты Меркурий на первой гравитационной орбите (n = 1):

v1 = γ Mc / 2 h'.

Из уравнения смещения перигелия планеты выделим γ Mc:

γ Mc = δφ1 c2 r1(1 - e12) / 6 π

и подставим в формулу для v1:

v1 = [c2 r1(1 - e12) / 12 π h'] δφ1 = vгр × δφ1,

где

vгр = c2 r1(1 - e12) / 12 π h'.

Величина смещения δφ1 мала и выражается в радианах. Выражение c2r1(1 - e12) / 12 π h' имеет размерность скорости. Перечислим ранее полученные формулы:

vэ = α c - для электрического поля протона в атоме водорода,

vм = α2 c - для магнитного поля протона в атоме водорода,

v1 = vгр δφ1 - для гравитационного поля Солнца.

Формулу

vгр = c2 r1(1 - e12) / 12 π h' = v1 / δφ1

можно интерпретировать как скорость гравитационных волн (гравитационных взаимодействий). Используя данные для Меркурия, получаем:

vгр ≈ (2,99×108)2×5,8×1010(1 - 0,2062) / 12×3,14×1,39×1015 ≈ 9,5×1010 м/с

или

vгр ≈ 318 c ,

т.е. скорость гравитационных волн в 318 раз больше скорости электромагнитных волн (света). Аналогично, как для электрического поля и магнитного поля α и c определяют размеры орбит в атоме водорода, скорость гравитационных волн vгр и смещение перигелия δφ определяют размеры планетных орбит Солнечной системы.

Скорость гравитационных волн на:

Страница: 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15 , 16 , 17 , 18

Примечания[править | править код]

См. также[править | править код]

Ссылки[править | править код]

Литература[править | править код]

Источник — https://traditio.wiki/w/index.php?title=Комплекс_%22Хеопс-Хефрен-Микерин%22%3D%22Атом_водорода%225&oldid=854081