Комплекс "Хеопс-Хефрен-Микерин"="Атом водорода"2
| Первоначальные исследования Этот раздел статьи является первичным источником части изложенной в нём информации, содержа первоначальные (или ранее не известные широкому кругу читателей) исследования. |
Движение электрона в магнитном поле[править | править код]
С момента введения понятия "электрон" в физике появился вопрос "Каковы размеры электрона или его надо считать точечным?". В зависимости от решаемых задач пользовались или тем, или другим понятием. Одновременно возникла и проблема определения понятий "электрон" и "Что принимать за размеры электрона?".
(Для египтологов, лингвистов, физиков, математиков: есть небольшая вероятность обнаружения записи в Комплексе пирамид, чем-то похожей на формулу α2 c = v, где v - скорость электрона в магнитном поле протона, α - постоянная тонкой структуры, c - скорость света).
Движение электрона в магнитном поле на:
- http://www.mirradio.info/2008/05/03/dvizhenie-jelektronov-v-jelektricheskom.html
- http://fiz.1september.ru/2006/04/02.htm
- http://www.atsuk.dart.ru/books_online/09ef_el_mag/text2.shtml
- http://www.elremont.ru/small_rbt/bt_rem17.php
- http://school-collection.edu.ru/catalog/res/53975236-cfaf-53ba-6f86-6b0e96e64683/?f..
- http://ru.wikipedia.org/wiki/Уровни_Ландау
Точечный электрон[править | править код]
Ранее мы выяснили, что электрон в электрическом поле в атоме водорода с n = 1 движется по первой боровской орбите с
- r0 = ħ2 / k' e2 m = ħ / α m c.
Введем две системы координат. Система XOY: центр масс (ЦМ) протон-электрон совпадает с точкой O. Система X'O'Y': электрон в точке O'.
На рисунке r0 = OO' - радиус первой боровской орбиты, rp = (me/mp)r0 - радиус орбиты протона.
В квантовании атома по Бору центр масс совпадает с протоном и поэтому протон покоится. Следовательно, такой протон не создает магнитного поля - вокруг него есть только электрическое поле. Это электрическое поле заставляет двигаться по орбите электрон и отсюда получаются значения r0, v0, T0 и т.д.
В идеальном же случае это не так. Протон и электрон совершают движения вокруг центра масс (= окружности). Точно также можно говорить и о движении (вращении) протона вокруг электрона и электрона - вокруг протона. Это зависит от рассматриваемых систем отсчета.
В случае взаимодействия протона с электроном обязательно появляются 3 несовпадающие точки - центр протона, центр электрона и центр масс. Следствием этого является существование в окружающем пространстве двух полей - электрического и магнитного полей. Следовательно, электрон, двигающийся по орбите вокруг протона, всегда находится под влиянием (= действием) электрического и магнитного полей.
Итак, протон двигается относительно электрона по круговой орбите с (r0 + rp). Этим движением создается круговой протонный ток, который, в свою очередь, создает магнитное поле в области, где расположен электрон (точнее - вектор магнитной индукции Bp):
- Bp = (μ0 / 2) [Ip / (r0 + rp)],
где μ0 - магнитная постоянная, Ip - сила тока (протонный ток), обусловленная движением протона вокруг электрона. Сила тока Ip может быть выражена через заряд протона e и период Tp обращения протона вокруг электрона:
- Ip = e / Tp.
Период обращения протона Tp вокруг электрона равен периоду обращения электрона Te вокруг протона:
- Tp = Te = T0 = (2 π r0) / v0,
где v0 - скорость электрона на первой боровской орбите. Тогда
- Bp = (μ0 / 2)[e / T0(r0 + rp)] = (μ0 / 2)[e / (2 π r0/ v0)(r0 + rp)] = μ0 e v0 /4 π r0(r0 + rp).
Так как в этой формуле правая часть = const, то движение электрона происходит в постоянном магнитном поле, т.е. по окружности. Следовательно, на движение электрона в электрическом поле протона по орбите с r0 накладывается действие магнитного поля протона. Это наложение магнитного поля приводит к появлению дополнительной скорости электрона - скорости электрона относительно магнитного поля протона (v). Тогда применяем условие для электрона:
- Fл = F,
где Fл - сила Лоренца, действующая на электрон. Далее получаем
- e v0 Bp = m v2 / r0,
где v - скорость электрона относительно магнитного поля на первой боровской орбите, m - масса электрона. Делая вместо Bp подстановку, имеем:
- e v0 [μ0 e v0 / 4 π r0(r0 + rp)] = m v2 / r0 или μ0 e2 v02 / 4 π (r0 + rp) = m v2.
Откуда получаем
- v2 = μ0 e2 v02 / 4 π m(r0 + rp).
Так как
- r0 = 4π ε0 ħ2 / e2 m, μ0 = 1 / ε0 c2,
то соответственно
- v2 = e2 v02 / 4 π m ε0 c2 [(4 π ε0 ħ2 / e2 m) + rp)].
После преобразований получаем:
- v2 = α2 v02 ħ / ħ + α c m rp, где α = e2 / 4π ε0 ħ c.
Учитывая, что ħ >> α c m rp, имеем
- v2 = α2 v02 ==> v = α v0 ==> v = α2 c.
Окончательно
- vм = v = αv0 = α2c ≈ 16 км/с.
Значит, наличие магнитного поля протона ведет к появлению дополнительной скорости vм для электрона - α2c - на первой боровской орбите.

Для анализа
- α c = vэ≈2187км/с: связь скорости света и скорости электрона на первой боровской орбите под действием электрического поля;
- α2 c = vм≈16км/с: связь скорости света и скорости электрона на первой боровской орбите под действием магнитного поля;
- α vэ = vм: связь скорости электрона на первой боровской орбите под действием электрического поля и скорости электрона на первой боровской орбите под действием магнитного поля;
- значки "э" и "м" при сравнении не учитывать.
Найдем дополнительный путь электрона Lм при движении в магнитном поле движущегося протона за время T0 полного оборота электрона по первой боровской орбите:
- Lм = vм T0 = α2 c (2 π ħ3 / k'2 e4 m).
Массу электрона выразим из формулы для первого боровского радиуса:
- m = ħ2 / k' e2 r0.
Тогда
- Lм = α2 c [2 π ħ3 / k'2 e4 (ħ2 / k' e2 r0)] = α2 c (2 π ħ / k' e2) r0 = α2 (4 π ε0 ħ c / e2)2 π r0 = (α2 / α)2 π r0 = 2 π α r0.
Отсюда получаем
- Lм / 2 π r0 = α.
Пройденный путь в магнитном поле во много раз меньше пройденного пути в электрическом поле, т.к. α - малая величина:
- Lм << 2 π r0.
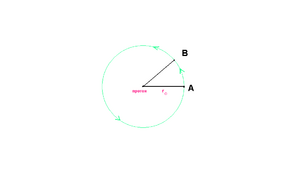
Значит, при наличии только электрического поля протона электрон делает полный оборот вокруг протона: L0 = 2 π r0. Но в действительности на электрон действует еще и магнитное поле протона (учет центра масс). Поэтому электрон оказывается не в точке А, а попадает в точку В по какой-то траектории. Если бы электрон двигался по эллиптической орбите, то это можно было бы рассматривать как смещение периядра (ближайшая точка эллиптической электронной орбиты к ядру в атоме водорода) электрона. (В общей теории относительности в уравнении для смещения перигелия планеты δφ существует и при эксцентриситете орбиты e = 0).
Точечный электрон на:
- http://lit.lib.ru/s/shaljapin_a_l/text_0310.shtml
- http://ru.wikipedia.org/wiki/Фотон
- http://humandesign.us/06/292.html
- http://library.mephi.ru/data/scientific-sessions/2000/5/417.html
- http://www.hizone.info/?di=200606192
Протяженный электрон[править | править код]
Предположим, что точечный электрон (= элементарный электрический заряд) при движении по первой боровской орбите в электрическом поле протона со скоростью v0 = αc (радиус r0) и с дополнительной скоростью vм = α2c, обусловленную наличием магнитного поля протона (O2O3 = R - смещение электрона), совершает круговое движение вокруг O3 (радиус l). Масштаб расстояний не соблюден.
Предполагая также, что за процессы, происходящие внутри орбиты радиуса l ответственно слабое взаимодействие и, принимая во внимание установленную взаимосвязь электромагнитных и слабых взаимодействий, можно считать: вращение точечного электрона вокруг O3 происходит под действием слабых сил или ≈ магнитных сил.
Тогда вокруг точки O3 вращается протон, создающий магнитную индукцию ↑B в точке O3. Если O2O3 = R << r0, то магнитное поле в области O2 с радиусом R можно считать квазиоднородным. Точечный электрон, вращающийся вокруг O3, создает магнитную индукцию ↑B1 в точке O3. По принципу суперпозиции полей, получаем:
- B' = B + B1 или ↑B' = ↑B + ↑B1.
Магнитная индукция, созданная протоном в O3:
- B = μ0 e v0 / 4 π r02.
Магнитная индукция, созданная точечным электроном в O3:
- B1 = - μ0 e v / 4 π l2,
где v - скорость движения точечного электрона в магнитном поле по орбите радиуса l. Тогда
- B' = B - B1.
Если |↑B| << |↑B1|, то пренебрегаем B:
- B' = B1
(без учета знаков B' и B1, т.к. необходимо находить l). Учитывая
- Fл = F,
получаем
- μ0 e v2 / 4 π l2 = m v2 / l.
Отсюда находим (учитывая, что μ0 = 1 / ε0c2):
- l = μ0 e2 / 4 π m = e2 / 4 π ε0 c2 m.
Массу m электрона выражаем из формулы первого боровского радиуса:
- m = 4 π ε0 ħ2 / e2 r0.
Тогда
- l = e2 / [4 π ε0 c2 (4 π ε0 ħ2 / e2 r0)] = (e4 / 16 π2 ε02 c2 ħ2) r0 = α2 r0.
- l = re = α2r0 ≈10−15 м - классический радиус электрона.
Получается, что точечный электрон создает протяженный электрон.
Выводы по движению точечного электрона в магнитном поле
- наличие магнитного поля протона приводит к смещению точечного электрона;
- размер протяженного электрона определяется в какой-то степени слабым взаимодействием (≈магнитная сила);
- условие ↑B' = ↑B + ↑B1 - условие существования слабых сил во внутренней области радиуса l (= re).
Итог из вышеизложенного
Автор: Тест на логику мышления → Чистота проведения теста зависит от Вас самих.
Проведение:
- а) как на экзамене: чистый лист бумаги - ручка (карандаш) - Ваша голова;
- б) текст - предложения теста - расположите под верхним краем экрана, чтобы Вам не мешал вышеизложенный материал;
- в) ответы на предложения теста (I-III) - за 1 присест;
- г) предложения теста даны в словесной форме (словами) и Вам необходимо их записать сокращенно - в виде уравнений, формул, значков, эскизов, рисунков и т.п., т.е. стараться максимально их упростить и укоротить.
Условие теста:
- I Какая-то угловая величина (= угол) умножается на диаметр первой боровской орбиты электрона и получается диаметр орбиты электрона в магнитном поле протона;
- II Эта же угловая величина (= угол) умножается на диаметр орбиты электрона в магнитном поле протона и получается классический диаметр электрона;
- III Объедините эти Ваши две записи в одну запись.
Проверка:
- а) сравните Вашу III запись с записью на пирамиде Хеопса (на фото лучше);
- б) проверьте правильность записей автора - I и II содержание) - по текстам "Движение электрона в электрическом и магнитном полях протона".
Протяженный электрон на:
- http://web.archive.org/web/20060619055301/http://elefzaze.boom.ru/indx0605ru.html
- http://www.biografija.ru/
- http://nuclphys.sinp.msu.ru/enc/e092p01.htm
- http://www.tamm.lpi.ru/seminars1/archive/vas_05.html
Постоянная тонкой структуры на:
- http://ru.wikipedia.org/wiki/Постоянная_тонкой_структуры
- http://elementy.ru/news/430291
- http://www.scientific.ru/journal/news/n271201.html
- http://kosinov.314159.ru/kosinov10.htm
- http://nature.web.ru/db/msg.html?mid=1177057
- http://web.archive.org/web/20040916185955/http://radon.boom.ru/alfa.htm
- http://science.compulenta.ru/280145/
- http://www.zero-gravity.ru/article/archiw/fizika/
- http://www.cnews.ru/newsline/index.shtml?2005/04/20/177458
Страница: 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15 , 16 , 17 , 18
Примечания[править | править код]
См. также[править | править код]
Ссылки[править | править код]
Литература[править | править код]
- Физический энциклопедический словарь. М."Советская энциклопедия". 1983
- Л.Д.Ландау, Е.М.Лифшиц. Теоретическая физика. //Теория поля.Т.II.М."Наука". 1988
- В.Б.Берестецкий, Е.М.Лифшиц, Л.П.Питаевский. Теоретическая физика//Квантовая электродинамика.Т.IV.М."Наука". 1989
- Ю.А.Храмов. Физики//Биографический справочник.М."Наука". 1983
- О.П.Спиридонов. Универсальные физические постоянные.М."Просвещение". 1984
- Л.Р.Стоцкий. Физические величины и их единицы.М."Просвещение".1984
- Дж.Нарликар. Гравитация без формул/перев. с англ./.М."Мир". 1985
- В.Л.Гинзбург. О физике и астрофизике.М."Наука". 1985
- В.Чолаков. Нобелевские премии//Ученые и открытия/перев. с болг./.М."Мир". 1987
- В.П.Цесевич. Что и как наблюдать на небе.М."Наука". 1984
- И.С.Шкловский. Вселенная.Жизнь.Разум.М."Наука". 1987
- Б.А.Воронцов-Вельяминов. Очерки о Вселенной.М."Наука". 1980
- Я.Б.Зельдович, И.М.Яглом. Высшая математика//Для начинающих физиков и техников.М."Наука". 1982
- Г. Корн, Т. Корн. Справочник по математике//Для научных работников и инженеров/перев. с амер./.М."Наука". 1984