Комплекс "Хеопс-Хефрен-Микерин"="Атом водорода"14

Материал из свободной русской энциклопедии «Традиция»
Перейти к навигации Перейти к поиску
Periss icon.png Первоначальные исследования
Этот раздел статьи является первичным источником части изложенной в нём информации, содержа первоначальные (или ранее не известные широкому кругу читателей) исследования.

[править | править код]

Итак, вначале взаимодействия не было — у тела m кинетическая энергия K и потенциальная энергия П равны 0. Энергия связи также Eсв = 0, так как системы M ↔ mc нет. Тело обладает только E0 ≠ 0 (собственная энергия тела). Тогда полная энергия Eполн' тела m (вводя штрих для первого состояния):

Eполн' = K' + П' + E0 + Eсв' .

В Солнечной же системе (зона взаимодействия) тело m обладает уже как кинетической K, так и потенциальной П энергиями относительно Mc (ЦМ), а также собственной энергией E0. Если тела взаимодействуют гравитационно, то по первому закону Кеплера Mc и m станут двигаться вокруг центра масс (ЦМ). Тогда полная энергия Eполн' ' (два штриха — второе состояние) тела m будет равна:

Eполн' ' = K' ' + П' ' + E0 + Eсв' ' ,

где

Кинетическая энергия K, потенциальная энергия П и энергия связи Eсв обусловлены взаимодействием тел.

Согласно закону сохранения и превращения энергии для замкнутой Вселенной:

Eполн' = Eполн' '

или

K' + П' + E0 + Eсв' = K' ' + П' ' + E0 + Eсв' ' .

Учитывая, что K' = П' = Eсв' = 0, получаем:

0 = K' ' + П' ' + Eсв' ' .

Откуда

Eсв' ' = - (K' ' + П' ') .

Так как в системе два тела, то энергия связи распределяется между m и Mc поровну. Энергия связи, приходящаяся на одно тело:

Eсв = Eсв' ' / 2 = - (K' ' + П' ') / 2 .

Опуская штрихи, получаем:

Eсв = - (K + П) / 2 .

Зная энергию связи Eсв, нетрудно рассчитать соответствующую ей массу - "добавочную" массу:

Δm = Eсв / c2 = - (K + П) / 2 c2 .

Солнечная система - гравитационное поле[править | править код]

Eсв = - (K + П) / 2 = - (m v2 / 2 - γ Mc m / r) / 2 = (γ Mc m / r - m v2 / 2) / 2 .
Δ m = (γ Mc m / r - m v2 / 2) / 2 c2 .

Для Меркурия (n = 1, r = 58 млн. км, m = 3,3×1023 кг, v = 48 км/с):

γ Mc m / 2 c2 r = 6,7×10-11×1,9×1030×3,3×1023 / 2×(3×108)2×5,8×1010 = 4,0×1015 (кг);
(1 / 4) m (v / c)2 = (1 / 4) × 3,3 × 1023 × (4,8 × 104 / 3 × 108)2 = 2,1 × 1015(кг).

В общем же случае Π = 2|K|. Если Eсв = 0, то

γ Mc m / 2 c2 r - (1 / 4) m (v / c)2 = 0 .

Откуда

vэл (= v) = (2 γ Mc / r)1/2 = (2)1/2 v' ,

где

Так как П = 2|K|, то

Eсв = γ Mc m / 4 r

и

Δ m = γ Mc m / 4 c2 r - "добавочная" масса для Солнца и планет.

Истинные значения масс Солнца и планет тогда равны:

Mc' = Mc + Δ m = Mc + γ Mc mn / 4 c2 r ;
mn' = mn + Δ m = mn + γ Mc mn / 4 c2 r .

Следовательно, в точных расчетах по Солнечной системе эти добавки необходимо учитывать.

Стоит добавить еще, что если добавки Δ m к массам m и Mc не учитывать, т.е. Δ m = 0, то получается закон всемирного тяготения Ньютона:

F = γ (Mc + Δ m)(m + Δ m) / r2 ==> F = γ Mc m / r2 .

Солнечная система на:

Атом водорода - электромагнитное поле[править | править код]

Eсв = - (1 / 2) (K + П) = - (1 / 2) (m v2 / 2 - k' e2 / r) = (1 / 2) (k' e2 / r - m v2 / 2) .
Δ m = (1 / 2 c2) (k' e2 / r - m v2 / 2) = k' e2 / 2 c2 r - (1 / 4) m (v / c)2 .

Для электрона (n = 1, a0 = 5,3×10−11 м, v0 = α c = 2,1×106 м/с, me = 9,1×10−31 кг, e = 1,6×10−19 Кл) получаем:

(1 / 4) m (v / c)2 = (1 / 4) me α2 = (1 / 4) × 9,1 × 10-31 × (7,3 × 10-3)2 = 1,2 × 10-35 (кг) .

Такое выражение использовалось в вычислениях аномального магнитного момента электрона (АММЭ).

k' e2 / 2 c2 r = 9 × 109 × (1,6 × 10-19)2 / 2 × (3 × 108)2 × 5,3 × 10-11 = 2,4 × 10-35 (кг) .

В общем же случае Π = 2|K|. Если Eсв = 0, то

k' e2 / 2 c2 r - (1 / 4) me (v / c)2 = 0 .

Откуда

vэл (= v) = (2 k' e2 / me r)1/2 = (2)1/2 v' ,

где

Так как П = 2|K|, то

Eсв = (1 / 4) m v2

и

Δ m = (1 / 4) m (v / c)2 = (1 / 4) me α2 .

Тогда истинные значения масс протона и электрона равны:

mp' = mp + Δ m = mp + (1 / 4) me α2 ,
me' = me + Δ m = me + (1 / 4) me α2 .

Именно эти формулы применяются при вычислении аномального магнитного момента электрона (АММЭ). Гравитационной "добавкой" γ mp me / 4 c2 r ~ 10−75 кг можно пренебречь. В атоме водорода Δ m создается за счет кинетической и потенциальной энергий, которые, в свою очередь, "получаются" из окружающей атом водорода электромагнитной энергии. Добавка со стороны магнитного поля (МП) также мала и поэтому здесь не рассматривалась.

Атом водорода на:

Третий закон Кеплера с учетом уточненного первого закона Кеплера[править | править код]

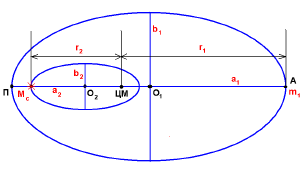
Геометрическая иллюстрация уточненного первого закона Кеплера

Пояснения к рисунку:

Рассматриваем движение планеты m1 относительно Солнца Mc как движение планеты m1 относительно ЦМ:

  • Mc' = Mc + Δ m = Mc + γ Mc m1 / 4 c2 r ;
  • m1' = m1 + Δ m = m1 + γ Mc m1 / 4 c2 r .

Следовательно, с одной стороны, сила притяжения между Mc' и m1' равна:

Fгр = γ Mc' m1' / acp2 = γ (Mc + γ Mc m1 / 4 c2 r) (m1 + γ Mc m1 / 4 c2 r) / acp2 = (γ Mc m1 / acp2)(1 + γ m1 / 4 c2 r)(1 + γ Mc / 4 c2 r) ,

где aср - среднее расстояние между Mc и m1 (= r1 = r). С другой стороны:

F = (m1 + γ Mc m1 / 4 c2 r)v1 cp2 / acp = (m1 v1 cp2 / acp) (1 + γ Mc / 4 c2 r) ,

где v1 cp - средняя скорость планеты на орбите. Эту скорость найдем с помощью уравнения

v1 cp = π (a1 + b1) / T1 = π a1 [1 + (1 - e12)1/2] / T1 ,

где T1 - звездный период обращения планеты относительно ЦМ, e1 - эксцентриситет внешнего эллипса. Согласно ранее выведенной формуле

acp = a1 + a2 = a1 [1 + {e3 / (1 + e3)} {(1 + e1) / (1 + e2)}] ,

где e3 = m1 / Mc , e2 - эксцентриситет внутреннего эллипса. Тогда

vcp2 = (π2 / T12) a12 [1 + (1 - e12)1/2]2 .

Далее имеем

Fгр = F

или

γ (Mc m1 / acp2) (1 + γ m1 / 4 c2 r) (1 + γ Mc / 4 c2 r) = (m1 v1 cp2 / acp) (1 + γ Mc / 4 c2 r) .

После сокращений:

(γ Mc / acp) (1 + γ m1 / 4 c2 r) = v1 cp2 .

Члены

γ Mc / 4 c2 r , γ m1 / 4 c2 r

для Солнца и планет находятся в интервале 10−8 - 10−11. Эти члены можно не учитывать и тогда, продолжая, получаем:

γ Mc / a1 [1 + {e3 / (1 + e3)} {(1 + e1) / (1 + e2)}] = (π2 / T12) a12 [1 + (1 - e12)1/2]2

или

γ Mc T12 / π2 = a13 [1 + {e3 / (1 + e3)} {(1 + e1) / (1 + e2)}] [1 + (1 - e12)1/2]2 .

По аналогии для системы Mc ↔ m2 имеем (штрих введен для второй планеты m2):

γ Mc T22 / π2 = a23 [1 + {e3' / (1 + e3')} {(1 + e1') / (1 + e2')}] [1 + (1 - e1'2)1/2]2 ,

где

  • e3' = m2 / Mc ;
  • e1' и e2' - эксцентриситеты внешнего и внутреннего эллипсов планеты m2 и Солнца Mc .

Для упрощения дальнейших расчетов необходимо сделать ряд допущений:

  • движение Солнца в парах по отдельности (Mc ↔ m1 и Mc ↔ m2) и при совместном движении (Mc ↔ m1 ↔ m2) примерно одинаково - движение по эллипсу (в случае совместного движения Mc ↔ m1 ↔ m2, строго говоря, форма орбит - не эллипсы, а более сложные кривые) ;
  • слабое гравитационное взаимодействие между m1 и m2 (Fгр ≈ 0) .

Окончательно получаем:

(T1 / T2)2 = (a1 / a2)3 [[1 + {e3 / (1 + e3)} {(1 + e1) / (1 + e2)}] / [1 + {e3' / (1 + e3')} {(1 + e1') / (1 + e2')}]] [{1 + (1 - e12)1/2} / {1 + (1 - e1'2)1/2}]2 .

Если e1 = e2 (e1' = e2'), то 1 + e1 = 1 + e2 (1 + e1' = 1 + e2'). Учитывая, что e3 = m1 / Mc и e3' = m2 / Mc, имеем:

1 + [e3 / (1 + e3)] [(1 + e1) / (1 + e2)] = 1 + [e3 / (1 + e3)] = (1 + 2 e3) / (1 + e3) = (1 + 2 m1 / Mc) / (1 + m1 / Mc) = (Mc + 2 m1) / (Mc + m1) ,
1 + [e3' / (1 + e3')] [(1 + e1') / (1 + e2')] = 1 + [e3' / (1 + e3')] = (1 + 2 e3') / (1 + e3') = (1 + 2 m2 / Mc) / (1 + m2 / Mc) = (Mc + 2 m2) / (Mc + m2) .

Тогда

(T1 / T2)2 = (a1 / a2)3 [{(Mc + 2 m1) / (Mc + m1)} / {(Mc + 2 m2) / (Mc + m2)}] [{1 + (1 - e12)1/2} / {1 + (1 - e1'2)1/2}]2

или

(T1 / T2)2 [(Mc + m1) / (Mc + m2)] = (a1 / a2)3 [(Mc + 2 m1) / (Mc + 2 m2)] [{1 + (1 - e12)1/2} / {1 + (1 - e1'2)1/2}]2 .

Обозначая e1' как e2 , получаем окончательно: T 1 2 T 2 2 M c + m 1 M c + m 2 = a 1 3 a 2 3 M c + 2 m 1 M c + 2 m 2 ( 1 + 1 − e 1 2 ) 2 ( 1 + 1 − e 2 2 ) 2 . \frac{T_1^2}{T_2^2} \frac{M_c + m_1}{M_c + m_2} = \frac{a_1^3}{a_2^3} \frac{M_c + 2 m_1}{M_c + 2 m_2} \frac{(1 + \sqrt{1 - e_1^2})^2}{(1 + \sqrt{1 - e_2^2})^2} .

Для проверки рассматриваем это последнее уравнение и Таблицу 1. Производим вычисления и приходим к следующему результату:

Таблица 11

N
п/п		 Меркурий-планета
e2 = 0,206		 Проверяемая формула Абсолютная погрешность
усл. ед.		 Относительная погрешность
%
1 Венера
e1 = 0,007		 6,25×1,0000022 = 5,83×1,0000042×1,02
6,25 = 5,94		 - 0,31 4,0
2 Земля
e1 = 0,017		 16,81×1,0000029 = 15,63×1,0000056×1,02
16,81 = 15,94		 - 0,87 5,1
3 Марс
e1 = 0,093		 60,84×1,0000001 = 59,32×1,0000003×1,01
60,84 = 59,91		 - 0,93 1,5
4 Юпитер
e1 = 0,048		 2401×1,0009552 = 2197×1,0019105×1,02
2403 = 2244		 - 159 6,6
5 Сатурн
e1 = 0,054		 14884×1,0002858 = 13824×1,0005717×1,01
14888 = 13969		 - 919 6,1
6 Уран
e1 = 0,046		 122500×1,0000436 = 112749×1,0000873×1,02
122505 = 115014		 - 7492 6,1
7 Нептун
e1 = 0,008		 470596×1,0000514 = 456533×1,0001003×1,02
470644 = 465709		 - 4911 1,0
8 Плутон
e1 = 0,253		 1065024×0,9999998 = 1061208×0,9999996×0,994
1065023 = 1055839		 - 9184 0,8

Из сравнения всех известных и полученных формул третьего закона Кеплера следует, что самой оптимальной будет последняя формула. Увеличивать точность можно и далее, рассматривая дополнительные условия, но я ограничусь этой формулой.

Третий закон Кеплера на:

Страница: 0 , 1 , 2 , 3 , 4 , 5 ,6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15 , 16 , 17 , 18

Примечания[править | править код]

См. также[править | править код]

Ссылки[править | править код]

Литература[править | править код]

Источник — https://traditio.wiki/w/index.php?title=Комплекс_%22Хеопс-Хефрен-Микерин%22%3D%22Атом_водорода%2214&oldid=853947