Комплекс "Хеопс-Хефрен-Микерин"="Атом водорода"8
| Первоначальные исследования Этот раздел статьи является первичным источником части изложенной в нём информации, содержа первоначальные (или ранее не известные широкому кругу читателей) исследования. |
[править | править код]
При наличии орбитальных скоростей протона и электрона эти 2 сферы уже не будут совпадать. Вначале по орбите будет двигаться гравитационная сфера (протон), а за ней - электромагнитная сфера.
Электромагнитную сферу за пределами гравитационной сферы назовём "призраком" электрона. "Призрак" электрона - электромагнитный виртуальный посредник между протоном и электроном.
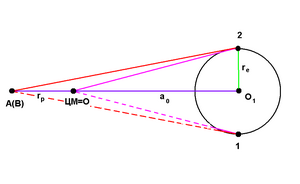
В I положении точки электрона 1 и 2, испуская виртуальные фотоны, ограничивают поток виртуальных фотонов через центр масс (конус). В момент достижения ими электромагнитной сферы (точка В) сам электрон будет находиться во II положении.
Рассмотрим подробнее радиусы-векторы, связывающие эти две сферы и электрон.
Площадь, ометываемая радиусом-вектором ↑r (протон-электрон) распадается на:
- площадь, ометываемую электромагнитным радиусом-вектором
- ↑rэл = ↑AO + ↑OB + ↑BO2 = ↑AB + ↑OB2 ,
- площадь, ометываемую гравитационным радиусом-вектором
- ↑rгр = ↑AO2 = ↑AO + ↑OO2 .
Поэтому
- S(↑r) = S(↑rэл) + S(↑rгр) = S(↑AO + ↑OB + ↑BO2) + S(↑AO2).
В этом уравнении запись S(↑r) означает:
- площадь фигуры S, ометываемая радиусом-вектором ↑r при вращении вокруг какой-то точки (начала или конца этого вектора, вокруг произвольной точки и т.п.)
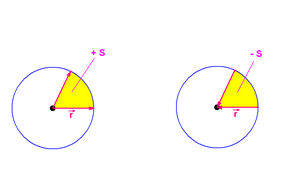
Ранее при вычислении площадей фигур, ометываемых радиусом-вектором (планетные и электронные орбиты) при вращении вокруг начала вектора, площади приписывался по умолчанию знак "+". Если тот же вектор будет описывать площадь фигуры при вращении вокруг конца этого вектора, то площадь необходимо брать со знаком "-". Наглядно это показано на рисунке.
"Призрак" электрона - виртуальный электромагнитный посредник между протоном и электроном. Поэтому ↑BO2 заменяется на ↑O2B и площадь, описываемая этим вектором, будет со знаком "-":
- ↑rэл = ↑AO + ↑OB - ↑O2B = ↑AB - ↑O2B.
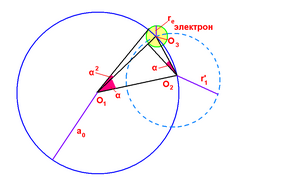
В случае протяженного электрона (re = α2 a0) необходимо учитывать и радиус-вектор самого электрона. Конец этого вектора - ↑re - описывает окружность (граница электрона). Вместо вектора ↑O2B тогда будет, например, вектор ↑1B. При вращении точки 1 вокруг электрона будут меняться и ↑1B и re. Ометываемая при этом фигура (приблизительно) - Δ 1B2, площадь которой вычисляется просто.
В итоге тогда имеем:
- S(↑r) = S(↑rэл) + S(↑rгр) = S(↑AO + ↑OB - ↑O2B) + S(↑AO + ↑O O2) = S(↑AO) + S(↑OB) - S(↑O2B) + S(↑AO) + S(↑OO2).
Площади S(↑AO) ≈ S(↑OB) ≈ 0 и их можно не учитывать. Остается:
- S(↑r) = S(↑OO2) - S(↑O2B).
Для упрощения вычислений сделаем перенос точки B в точку A и получаем:
- S(↑OO2) = 2 S(Δ O1 O 2) = 2 (1/2)a0 re = a0 re ,
- S(↑O2B) = 2 S(Δ A 2 O1) = 2 (1/2) (rp + a0)re = re (rp + a0) .
Окончательно имеем:
- S(↑r) = a0 re - re (rp + a0) = - re rp .
Двойка появилась в формулах потому, что Δ A 1 2 и Δ O 1 2 равнобедренные. Заменяя re = α2 a0 и rp = (me / mp) a0 , имеем:
- S(↑r) = - α2 (me / mp) a02 .
Ранее в написанной формуле для АММЭ
- μан / μБ = [Sэлл / π a02] + [S(FП1П2) / π a02] + [Sp / π a02] + [Se / π a02]
обозначение Se следует понимать как S(↑re):
- Se = S(↑re) = - α2 (me / mp) a02 ,
где Se - площадь, описываемая радиусом-вектором электрона.
Подставляя вместо S (числители) соответствующие выражения, получаем:
- μан / μБ = [π a02 {1 - (me/mp)2}1/2] / π a02 + [(α/2) a02 {1 / 1 + (me/mp)}{1 - (me/mp)}2] / π a02 + [π a02 (me/mp)2] / π a02 - [α2 a02 (me/mp] / π a02.
Окончательно для АММЭ:
- μан / μБ = [1 - (me/mp)2]1/2 + (α/2 π) [1 / {1 + (me/mp}][1 - (me/mp)]2 + (me / mp)2 - (α2 / π) (me / mp) .
Следует еще раз напомнить, что ранее в некоторых пунктах были рассмотрены движения электрона по различным орбитам с радиусами a0, r1', re и расчеты производились при 1 обороте вокруг соответствующего центра. Размеры на рисунке не соблюдены.
При рассмотрении движения электрона в электрическом поле протона за 1 полный оборот электрона происходит одновременное смещение электрона на угол α. Это смещение мы интерпретировали как "движение" электрона в магнитном поле протона по окружности радиуса r1'. Исходя из таких представлений, приходим к выводу T0 = T1' и r1' = α a0. Если re = α2 a0 или re = α r1', то и Te = T1'. T0, T1', Te - периоды обращений вокруг O1, O2, O3 ("Протяженный электрон").
Физический аспект[править | править код]
Упростим сначала вышенаписанную формулу для АММЭ. Так как me / mp << 1, то, применяя разложения в степенные ряды, имеем:
- (1 - x2)1/2 = 1 - (1/2) x2 + (1/8) x4 - ... ,
- 1 / (1 + x) = 1 - x + x2 - ... ,
и, учитывая первые два члена, получаем:
- μан / μБ = 1 - (1 / 2)(me / mp)2 + (α / 2 π)[1 - (me/mp]3 + (me / mp)2 - (α2 / π) (me / mp) .
После раскрытия скобок и группировки следует:
- μан / μБ = 1 + (α / 2 π) - (α / 2 π)(2 α + 3)(me / mp) + (1 / 2 π)(3 α + π)(me / mp)2 - (α / 2 π)(me / mp)3 .
Учитывая, что
- (α / 2 π)(me / mp)3 ~ 10−13
и приравнивая его к 0, получим окончательно:
- μан / μБ = 1 + (α / 2 π) - (α / 2 π)(2 α + 3)(me / mp) + (1 / 2 π)(3 α + π)(me / mp)2 .
Будем учитывать члены более высокого порядка и тогда получим:
- 1 - (1 / 2)(me / mp)2 + (1 / 8)(me / mp)4 + (α/ 2 π)[1 - (me / mp) + (me / mp)2][1 - (me / mp)]2 + (me / mp)2 - (α2 / π) (me / mp) .
После раскрытия скобок, отбрасывания членов < 10−12 и группировки, имеем:
- μан / μБ = 1 + (α / 2 π) - (α / 2 π)(2 α + 3)(me / mp) + (1 / 2 π)(4 α + π)(me / mp)2 .
Физики из квантовой электродинамики и смежных разделов физики с большой гордостью приводят результат совпадения теоретических и экспериментальных значений для АММЭ как факт "прекрасного согласия" теории и эксперимента:
- μтеор = 1,00115965237(28), μэкс = 1,00115965241(21).
Теоретическое значение здесь подсчитано по формуле:
- μан / μБ = 1 + (α / 2 π) - 0,328478(α / π)2 + 1,184175(α / π)3
с учетом следующих значений для:
- α = 7,29735321×10−3, π = 3,141592653589.
Вычисления дают (с точностью до 10−12):
- 1 + 0,001161409634 - 0,000001772300 + 0,000000014840 = 1,001159652374.
Наряду с этим значением α, в физике было получено более точное(?) значение: α = 7,2973506×10−3. Это значение не надо отбрасывать и не замечать. Если произвести вычисления по этой же формуле, то получим:
- 1 + 0,001161409419 - 0,000001772298 + 0,000000014840 = 1,001159651961.
Обозначим эти значения α через αmax и αmin: αmax = 7,29735321×10−3 , αmin = 7,2973506×10−3.
Так как связь между μан / μБ и α почти линейная, то подсчитаем среднее значение μан / μБ:
- (μан / μБ)ср = (1,001159652374 + 1,001159651961) / 2 = 1,001159652167
или (μан / μБ)ср = 1,001159652167(±207), или (μан / μБ)ср = 1,00115965216(±21).
Как видно, только верхняя граница (16 + 21 = 37) очень близка к экспериментальному значению 41. Пренебрегая ±21, можно сказать, что 16 далеко отстоит от 41.
Все дальнейшие вычисления будут вестись по αmax (верхняя граница и с учетом ±21).
Наличие квадратного корня в формуле для АММЭ накладывает дополнительные ограничения. Чтобы получить результат с точностью до 10−12, необходимо, чтобы выражение под квадратным корнем вычислялось с точностью до 10−24. Вычисления по этой формуле производились с точностью до 10−48(10−50), т.е. учитывались 48(50) цифр после запятой.
Неупрощенная формула
- μан / μБ = [1 - (me / mp)2]1/2 + (α / 2 π) [1 / {1 + (me / mp)}] [1 - (me / mp)]2 + (me / mp)2 - (α2 / π) (me / mp)
дает следующий результат в вычислениях:
- 0,999999851695 + 0,001159513640 + 0,000000296608 - 0,000000009231 = 1,001159652712
или 1,00115965250(±21).
Аналогично для формулы:
- μан / μБ = 1 + (α / 2 π) - (α / 2 π)(2 α + 3) (me / mp) + (1 / 2 π)(4 α + π)(me / mp)2
имеем:
- 1 + 001161409834 - 0,000001906803 + 0,000000149681 = 1,001159652712
или 1,00115965250(±21).
Вышенаписанные упрощенные формулы и ряд других, и произведенные по ним вычисления дают право не применять их в дальнейшем, ибо они дают ступенчатое изменение цифр для АММЭ. Вычисления здесь велись, исходя из me / mp = 5,44617364×10−4.
Упростим формулу
- μан / μБ = [1 - (me / mp)2]1/2 + (α / 2 π) [1 / {1 + (me / mp)}] [1 - (me / mp)]2 + (me / mp)2 - (α2 / π) (me / mp) ,
введя обозначение A = me / mp и получая физическую часть АММЭ. Тогда
- μан / μБ = (1 - A2)1/2 + (α / 2 π) (1 - A)2 / (1 + A) + A2 - (α2 / π) A - геометрическая часть АММЭ.
Ранее произведенные вычисления предполагали, что me и mp - массы покоя электрона и протона. В действительности же, например, масса электрона другая. Согласно формуле v0 = α c, мы имеем скорость (при αmax) = 2187 км/с. Поэтому необходимо учитывать зависимость массы от скорости для движущегося электрона (СТО):
- me = m0(e) / [1 - (v02 / c2)]1/2 = m0(e) / [1 - (α2 c2 / c2]1/2 = m0(e) / (1 - α2)1/2 .
Тогда в обозначении получаем:
- A = [m0(e) / mp] [1 / (1 - α2)1/2] .
Масса протона изменяется мало и поэтому mp ≈ const, ибо vp << c. Оставим в обозначении A вместо m0(e) - me, подразумевая, что это масса покоя электрона.
- A = (me / mp) [1 / (1 - α2)1/2] .
Вычисления с учетом этой формулы дают:
- 0,999999851688 + 0,001159513589 = 0,000000296623 - 0,000000009231 = 1,001159652669
или 1,00115965245(±21).
Как было показано ранее, смещение электрона на первой боровской орбите в магнитном поле протона на угол α означает, что периядро (ближайшая точка эллиптической электронной орбиты в атоме водорода) вращается с какой-то скоростью. Скорость электрона при "вращении" в магнитном поле по окружности радиуса r1':
- vм = α v0 = α2 c ≈ 16 км/с .
Скорость вращения периядра:
- vм' = r1' / T0 = (ħ / m c}) / (2 π ħ3 / k'2 e4 m) = e4 / (32 π3 ε02 ħ2 c) = (e4 / 16 π2 ε02 ħ2 c2) (c / 2 π) = (α2 / 2 π) c ≈ 3 км/с .
Эта скорость много меньше vм, и поэтому зависимостью me(vм') можно пренебречь. Вместо vм' = α2 c / 2 π возьмем vм = α2 c в виду того, что:
- 16 км/с >> 3 км/с;
- запись vм = α2 c более простая.
Если вычисления для vм = α2 c дадут небольшое изменение в цифрах, то и, следовательно, для vм' = α2 c / 2 π - тем более, изменения будут еще меньше. Учтя эти условия, получим для массы электрона:
- me = m0(e) / [1 - {(α c + α2 c)2 / c2}]1/2 = m0(e) / [1 - {α2 c2(1 + α)2 / c2}]1/2 = m0(e) / [1 - α2 (1 + α)2]1/2 ,
где m0(e) - масса покоя электрона. Поэтому в обозначении будем иметь:
- A = (me / mp) [1 / {1 - α2 (1 + α)2}1/2] .
С учетом основной формулы (выведенной) для АММЭ вычисления дают следующий результат:
- 0,999999851687 + 0,001159513588 + 0,000000296624 - 0,000000009231 = 1,001159652668
или 1,00115965245(±21).
Изменения произошли в 12 знаке, и, значит, скорость vм' = α2 c / 2 π не играет большой роли. Эти изменения потребуются при сверхточных вычислениях. В дальнейшем вместо vм' = α2 c / 2 π будем пользоваться vм = α2 c.
Вычислим полную энергию электрона на первой боровской орбите. Она складывается из кинетической энергии движущегося электрона и потенциальной энергии взаимодействия протона и электрона:
- E = K + П = (me v02 / 2) - (k'e2 / a0).
Учитывая, что v0 = α c , k' = 1 / 4 π ε0 , α = e2 / 4 π ε0 ħ c , a0 = ħ2 / k' e2 me, получаем:
- E = (me α2 c2 / 2) - me α2 c2 = - (1 / 2)me α2 c2 .
Аномальный магнитный момент электрона на:
- http://www.scientific.ru/spark/muonanomaly.html
- http://ufn.ru/ru/articles/1949/11/b/
- http://lib.mexmat.ru/books/7057
- http://ru.wikipedia.org/wiki/Электрон
- http://revolution.allbest.ru/physics/00048992_0.html
- http://physics.vniim.ru/webco2/qed/m_enc/QED_and_FPC.html
- http://www.astronet.ru/db/msg/1172494
- http://heritage.sai.msu.ru/ucheb/Zemcov/Part_3_Hydrogen/Chapter_19/chapter_19.htm
- http://web.archive.org/web/20050322225848/http://www.cultinfo.ru/fulltext/1/001/008/060/306.htm
- http://femto.com.ua/articles/part_1/0151.html
Страница: 0 , 1 , 2 , 3 , 4 , 5 ,6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15 , 16 , 17 , 18
Примечания[править | править код]
См. также[править | править код]
Ссылки[править | править код]
Литература[править | править код]
- Физический энциклопедический словарь. М."Советская энциклопедия". 1983
- Л.Д.Ландау, Е.М.Лифшиц. Теоретическая физика. //Теория поля.Т.II.М."Наука". 1988
- В.Б.Берестецкий, Е.М.Лифшиц, Л.П.Питаевский. Теоретическая физика//Квантовая электродинамика.Т.IV.М."Наука". 1989
- Ю.А.Храмов. Физики//Биографический справочник.М."Наука". 1983
- О.П.Спиридонов. Универсальные физические постоянные.М."Просвещение". 1984
- Л.Р.Стоцкий. Физические величины и их единицы.М."Просвещение".1984
- Дж.Нарликар. Гравитация без формул/перев. с англ./.М."Мир". 1985
- В.Л.Гинзбург. О физике и астрофизике.М."Наука". 1985
- В.Чолаков. Нобелевские премии//Ученые и открытия/перев. с болг./.М."Мир". 1987
- В.П.Цесевич. Что и как наблюдать на небе.М."Наука". 1984
- И.С.Шкловский. Вселенная.Жизнь.Разум.М."Наука". 1987
- Б.А.Воронцов-Вельяминов. Очерки о Вселенной.М."Наука". 1980
- Я.Б.Зельдович, И.М.Яглом. Высшая математика//Для начинающих физиков и техников.М."Наука". 1982
- Г. Корн, Т. Корн. Справочник по математике//Для научных работников и инженеров/перев. с амер./.М."Наука". 1984